- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема дипломной работы: Исследование модели фрактального броуновского движения презентация
Содержание
- 1. Тема дипломной работы: Исследование модели фрактального броуновского движения
- 2. 1 Основные определения Непрерывный гауссовский процесс
- 3. 2 Моделирование ФБД Ковариационная функция ФГШ: Спектральная
- 4. 3 Оценка характеристик смоделированного фрактального гауссовского шума
- 5. 4 Оценка ФБД по наблюдениям в
- 6. 5 Фильтрация Калмана-Бьюси в диффер. системе с
Слайд 1Тема дипломной работы:
Исследование модели фрактального броуновского движения
Студент: X
Руководитель: X
Слайд 21
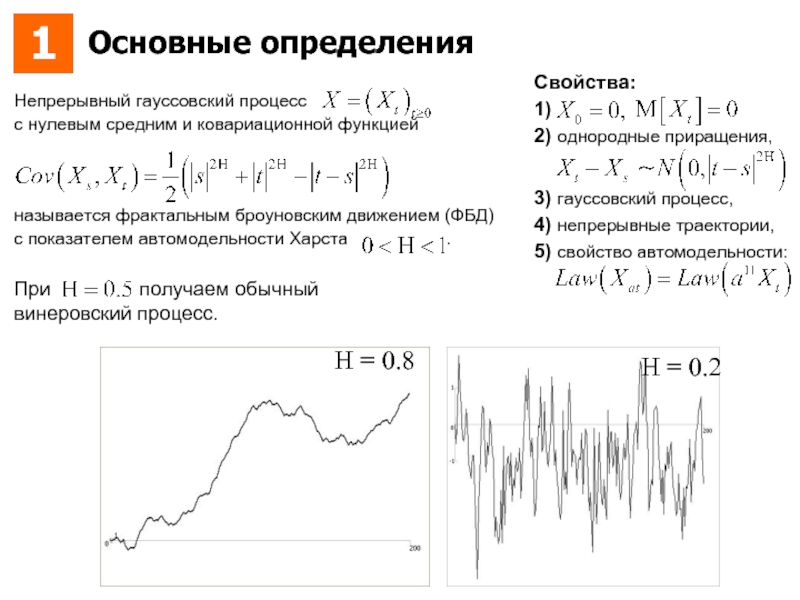
Основные определения
Непрерывный гауссовский процесс
с нулевым средним и ковариационной функцией
называется фрактальным
Н = 0.8
Н = 0.2
Свойства:
1)
2) однородные приращения,
3) гауссовский процесс,
4) непрерывные траектории,
5) свойство автомодельности:
Слайд 32
Моделирование ФБД
Ковариационная функция ФГШ:
Спектральная плотность
и ее аппроксимация:
, где
ФБД как сумма ФГШ:
Моделирование
Фрактальный гауссовский шум (ФГШ),
как разность ФБД:
Слайд 43
Оценка характеристик смоделированного
фрактального гауссовского шума
Оценка ковариационной функции:
где
Для реализации
в случае Н = 0.8
Для реализации
в случае Н = 0.2
Оценка параметра Харста по методу моментов:
Слайд 54
Оценка ФБД по наблюдениям
в двух точках
Теорема о нормальной корреляции:
где - оцениваемое значение,
- вектор наблюдений.
При Н = 0.5 получаем линейную оценку.
H = 0.8
H = 0.2
Слайд 65
Фильтрация Калмана-Бьюси в диффер.
системе с возмущениями в виде ФБД
Дифференциальная система,
описывающая
процесс
- ФБД.
Фильтр Калмана-Бьюси:
где
H = 0.8
H = 0.2