- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение тела под действием силы Стокса в вязкой среде презентация
Содержание
- 1. Движение тела под действием силы Стокса в вязкой среде
- 2. Цели работы нахождение подходящей среды для
- 3. Постановка задачи физическая постановка
- 4. Покоящееся тело (маленький шарик сферической формы диаметром
- 5. Математическая модель Можно сказать, вся математическая
- 6. Математическая модель Мы получаем две задачи
- 7. Условно эту часть работы можно разбить на
- 8. прорисовка шарика, координатной сетки, кнопок управления
- 9. Интерфейс регуляторы для ввода
- 10. Средства вывода динамические поля вывода
- 11. Проведение опытов выбор режима
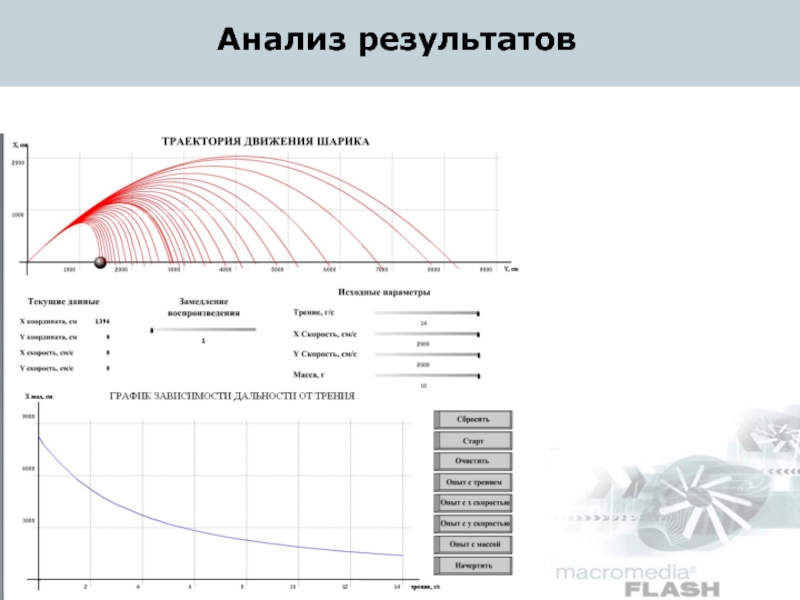
- 12. Анализ результатов
- 13. Результат работы демонстрация законов физики при
Слайд 2
Цели работы
нахождение подходящей среды для реализации таких типов задач
нахождение методов перехода
создание интерактивной среды, в которой пользователь может самостоятельно выполнять опыты в зависимости от некоторых данных (которые он сам и устанавливает)
Слайд 3Постановка задачи физическая постановка задачи цель моделирования
Разработка модели физическая модель математическая модель компьютерная модель
Компьютерный эксперимент проведение опытов анализ результатов
Этапы моделирования
Слайд 4Покоящееся тело (маленький шарик сферической формы диаметром ~ 1 cм), радиусом
F = k*V
Воспользуемся II законом Ньютона и составим следующие уравнения:
Физическая модель
m
x
y
..
..
=
m
0
g
-
k
y
x
.
.
Vx
Vy
.
.
=
-k/m
-k/m
0
0
Vx
Vy
+
0
g
Слайд 5
Математическая модель
Можно сказать, вся математическая модель сводится к решению двух уравнений,
Vx
=
-
k
m
Vx
.
Vy
.
-
k
m
Vy
=
+
g
Vx = x
Vx = x
.
.
..
Vy = y
Vy = y
.
.
..
y
..
-
k
m
y
=
+
g
.
x
=
-
k
m
x
..
.
Удобнее сразу решать следующие уравнения относительно координат
Слайд 6
Математическая модель
Мы получаем две задачи Коши:
x = -
x(0) = Vox
x(0) = xo
k
m
..
..
.
.
и
y = - y + g
k
m
y(0) = Voy
.
y(0) = yo
Решениями полученных систем являются:
x = xo+ - l-mt/k = xo + (1 – l-mt/k)
mVox
k
mVox
k
mVox
k
y = yo – g + m + t+( - )l-kt/m
m2
k2
Voy
k
gm
k
m2g
k2
mVoy
k
Слайд 7Условно эту часть работы можно разбить на три:
1)Создание главных объектов
2)Создание интерфейса
3)Разработка средств вывода результатов
Компьютерная модель
Слайд 8прорисовка шарика, координатной сетки, кнопок управления
Создание главных объектов
снабжение их программными кодами
первоначальное
Слайд 9
Интерфейс
регуляторы для ввода начальных данных
возможность управления временем
режимы проведения эксперимента
программная реализация
тестирование кода
Слайд 13
Результат работы
демонстрация законов физики при изучении нового материала (наглядное пособие);
проведение компьютерных
правильно действующая модель поведения тела