Фестиваль числовых функций
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
О, функция, как ты красива, умна! В науках и в жизни всегда ты нужна! презентация
Содержание
- 1. О, функция, как ты красива, умна! В науках и в жизни всегда ты нужна!
- 2. СЕГОДНЯ НА УРОКЕ повторим и приведем в
- 3. ПЛАН деятельности Повторение основных сведений об
- 4. Фестиваль числовых функций Фестиваль числовых функций
- 5. Регистрация участника Фестиваля
- 6. Графики Свойства Применение D(f) = (–∞;
- 7. Графики Свойства Применение D(f) = (–∞;
- 8. Графики Свойства Применение D(f) = (–∞;
- 9. Графики Свойства Применение D(f) = [0;
- 10. Графики Свойства Применение D(f) =
- 11. Графики Свойства Применение D(f) = (–∞;
- 12. Графики Свойства Применение D(f) = (–∞;
- 13. Графики Свойства Применение Формула E(f) =
- 14. Графики Свойства Применение D(f) = (–∞;
- 15. Графики Свойства Применение Формула Возрастает
- 16. Применение функций в науках и деятельности человека
- 17. Применение функций в науках и деятельности
- 18. Применение функций в науках и деятельности
- 19. Применение функций в науках и деятельности
- 20. Домашнее задание Алгебра 9
СЕГОДНЯ
НА УРОКЕ повторим и приведем в систему все знания о числовых функциях; узнаем: какую роль играют математические функции в науках и в жизни человека; научимся строить графики функций
Слайд 1«О, функция, как ты красива, умна!
В науках и в жизни всегда
ты нужна!»
Слайд 2СЕГОДНЯ
НА УРОКЕ
повторим и приведем в систему все знания о числовых функциях;
узнаем: какую роль играют математические функции в науках и в жизни человека;
научимся строить графики функций на компьютере;
применим свои знания в новых (незнакомых) ситуациях;
проверим свои знания с помощью теста
Фестиваль числовых функций
Слайд 3ПЛАН
деятельности
Повторение основных сведений об изученных функциях: работа в группах;
Знакомство с
информацией о применении функций параллельно с решением упражнений: защита мини-проектов групп, работа в парах с последующей самопроверкой;
Построение графиков функций на компьютере;
Проверка знаний: тестирование на компьютере;
Создание «Портфолио функции» в ходе урока.
Построение графиков функций на компьютере;
Проверка знаний: тестирование на компьютере;
Создание «Портфолио функции» в ходе урока.
Фестиваль числовых функций
Слайд 5Регистрация
участника
Фестиваля
Имя
Ник
Фото
Сведения о себе
Место работы (учебы)
Свойства
Применение
График
Формула
Название
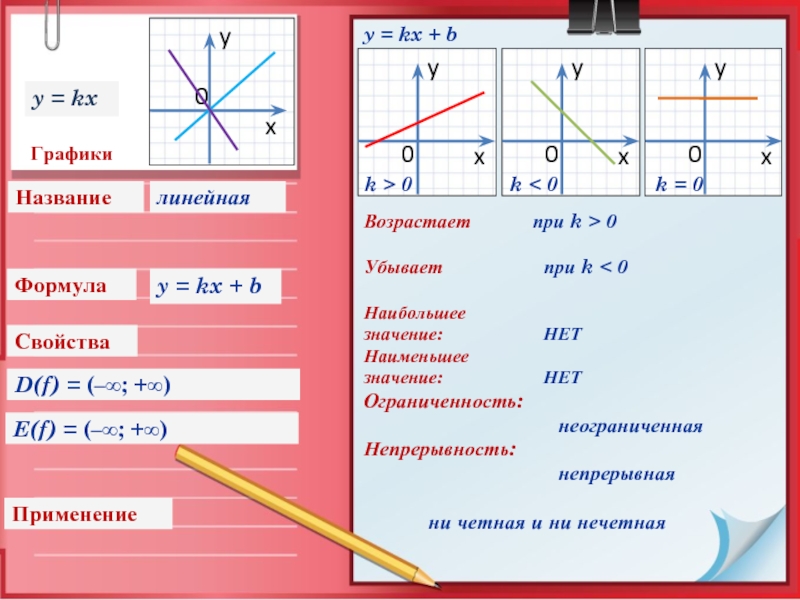
Слайд 6Графики
Свойства
Применение
D(f) = (–∞; +∞)
Формула
Название
E(f) = (–∞; +∞)
Возрастает
при k > 0
Убывает при k < 0
Наибольшее
значение: НЕТ
Наименьшее
значение: НЕТ
Ограниченность:
неограниченная
Непрерывность:
непрерывная
ни четная и ни нечетная
Убывает при k < 0
Наибольшее
значение: НЕТ
Наименьшее
значение: НЕТ
Ограниченность:
неограниченная
Непрерывность:
непрерывная
ни четная и ни нечетная
y = kx + b
k > 0 k < 0 k = 0
y = kx + b
y = kx
линейная
Слайд 7Графики
Свойства
Применение
D(f) = (–∞; +∞)
Формула
Название
E(f) = [0;+∞) при k >
0
Возрастает при k > 0 на [0; +∞)
Наибольшее значение: НЕТ
Наименьшее значение: унаим= 0
Убывает при k < 0 на (–∞; 0)
Наибольшее значение: унаиб= 0
Наименьшее значение: НЕТ
Ограниченность:
ограничена снизу при k > 0;
выпукла вниз
ограничена сверху при k < 0
выпукла вверх
Непрерывность: непрерывна
Нули функции: (0;0)
четная
y = kx2
y = kx2
квадратичная
k < 0
k > 0
E(f) = (–∞; 0] при k < 0
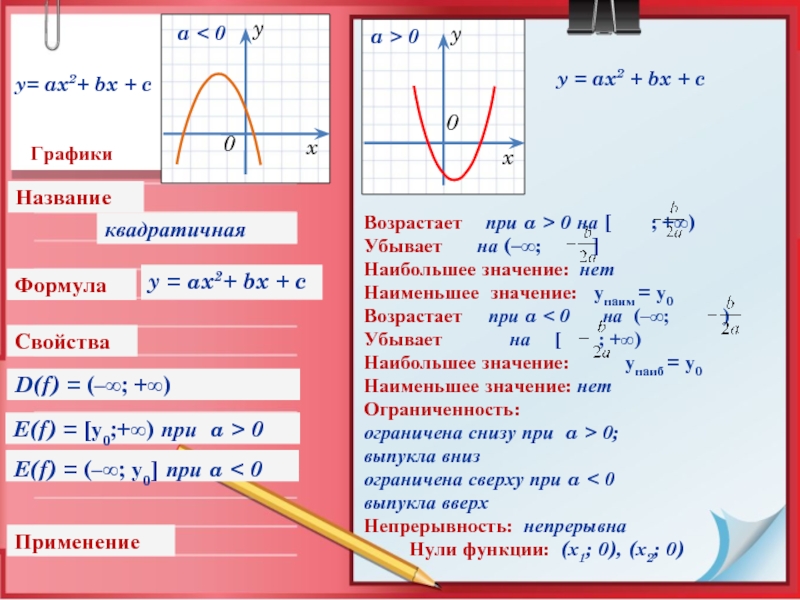
Слайд 8Графики
Свойства
Применение
D(f) = (–∞; +∞)
Формула
Название
E(f) = [у0;+∞) при a >
0
Возрастает при a > 0 на [ ; +∞)
Убывает на (–∞; ]
Наибольшее значение: нет
Наименьшее значение: унаим = у0
Возрастает при a < 0 на (–∞; )
Убывает на [ ; +∞)
Наибольшее значение: унаиб = у0
Наименьшее значение: нет
Ограниченность:
ограничена снизу при a > 0;
выпукла вниз
ограничена сверху при a < 0
выпукла вверх
Непрерывность: непрерывна
Нули функции: (х1; 0), (х2; 0)
квадратичная
E(f) = (–∞; у0] при a < 0
y = ax2 + bx + c
y= ax2+ bx + c
y = ax2+ bx + c
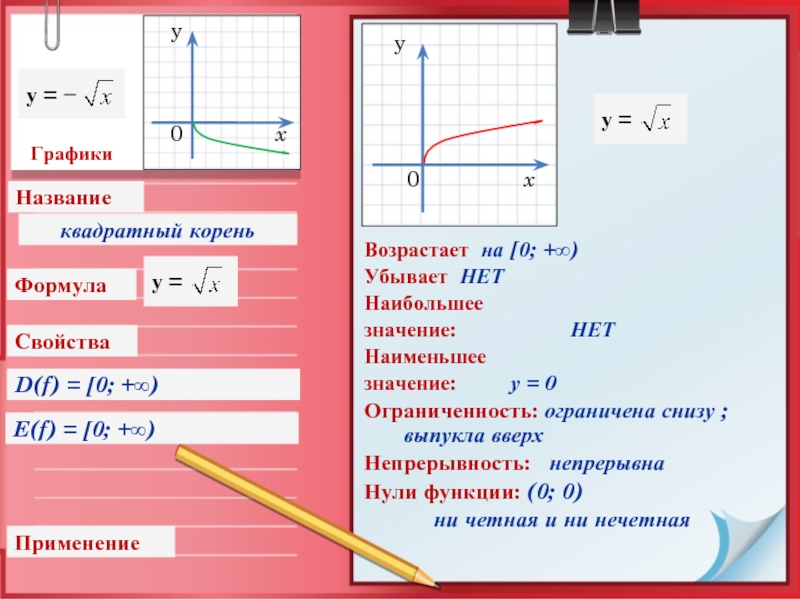
Слайд 9Графики
Свойства
Применение
D(f) = [0; +∞)
Формула
E(f) = [0; +∞)
Возрастает на
[0; +∞)
Убывает НЕТ
Наибольшее
значение: НЕТ
Наименьшее
значение: у = 0
Ограниченность: ограничена снизу ; выпукла вверх
Непрерывность: непрерывна
Нули функции: (0; 0)
ни четная и ни нечетная
Убывает НЕТ
Наибольшее
значение: НЕТ
Наименьшее
значение: у = 0
Ограниченность: ограничена снизу ; выпукла вверх
Непрерывность: непрерывна
Нули функции: (0; 0)
ни четная и ни нечетная
Название
квадратный корень
Слайд 10Графики
Свойства
Применение
D(f) =
Формула
E(f) =
Возрастает на
Убывает НЕТ
Наибольшее
значение:
НЕТ
Наименьшее
значение: НЕТ
Ограниченность: неограниченная
Непрерывность: непрерывная выпукла вниз на (–∞; 0]
выпукла вверх на [0;+∞)
Нули функции: (0;0)
нечетная
Наименьшее
значение: НЕТ
Ограниченность: неограниченная
Непрерывность: непрерывная выпукла вниз на (–∞; 0]
выпукла вверх на [0;+∞)
Нули функции: (0;0)
нечетная
Название
у =
кубический корень
(–∞; +∞)
(–∞; +∞)
у = −
(–∞; +∞)
Слайд 11Графики
Свойства
Применение
D(f) = (–∞; +∞)
Формула
Название
E(f) = [0;+∞)
Возрастает на [0; +∞)
Убывает на (–∞; 0]
Наибольшее значение: НЕТ
Наименьшее значение: унаим= 0
Ограниченность:
ограничена снизу
выпукла вниз
Непрерывность: непрерывна
Нули функции: (0;0)
четная
y = x2n
y = x2n
степенная с четным
показателем
y = - x2n
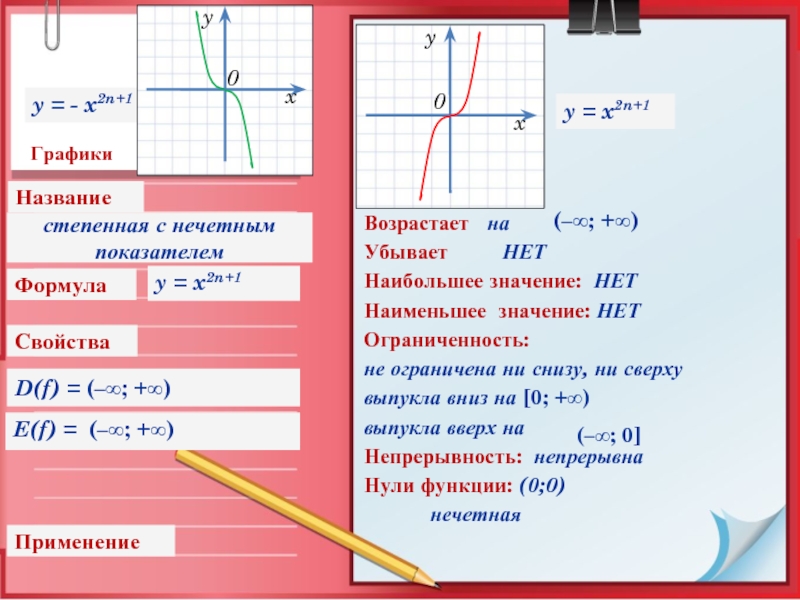
Слайд 12Графики
Свойства
Применение
D(f) = (–∞; +∞)
Формула
Название
E(f) = (–∞; +∞)
Возрастает
на
Убывает НЕТ
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
не ограничена ни снизу, ни сверху
выпукла вниз на [0; +∞)
выпукла вверх на
Непрерывность: непрерывна
Нули функции: (0;0)
нечетная
Убывает НЕТ
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
не ограничена ни снизу, ни сверху
выпукла вниз на [0; +∞)
выпукла вверх на
Непрерывность: непрерывна
Нули функции: (0;0)
нечетная
y = x2n+1
y = x2n+1
степенная с нечетным
показателем
y = - x2n+1
(–∞; +∞)
(–∞; 0]
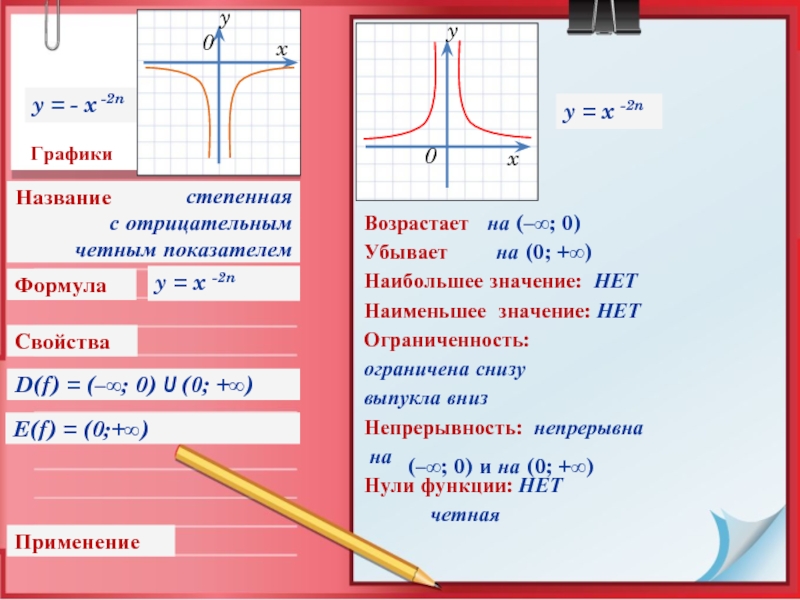
Слайд 13Графики
Свойства
Применение
Формула
E(f) = (0;+∞)
Возрастает на (–∞;
0)
Убывает на (0; +∞)
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
ограничена снизу
выпукла вниз
Непрерывность: непрерывна
на
Нули функции: НЕТ
четная
Убывает на (0; +∞)
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
ограничена снизу
выпукла вниз
Непрерывность: непрерывна
на
Нули функции: НЕТ
четная
y = x -2n
y = x -2n
степенная
с отрицательным
четным показателем
y = - x -2n
Название
D(f) = (–∞; 0) U (0; +∞)
(–∞; 0) и на (0; +∞)
Слайд 14Графики
Свойства
Применение
D(f) = (–∞; 0) U (0; +∞)
Формула
E(f) = (–∞;
0) U (0; +∞)
Возрастает при k < 0
на (–∞; 0) U (0; +∞)
Убывает при k > 0
на (–∞; 0) U (0; +∞)
Наибольшее
значение: НЕТ
Наименьшее
значение: НЕТ
Ограниченность: не ограничена
(не пересекает оси координат)
Непрерывность:
непрерывна на (–∞; 0) U (0; +∞)
Нули функции: нет
нечетная
у =
k > 0
k < 0
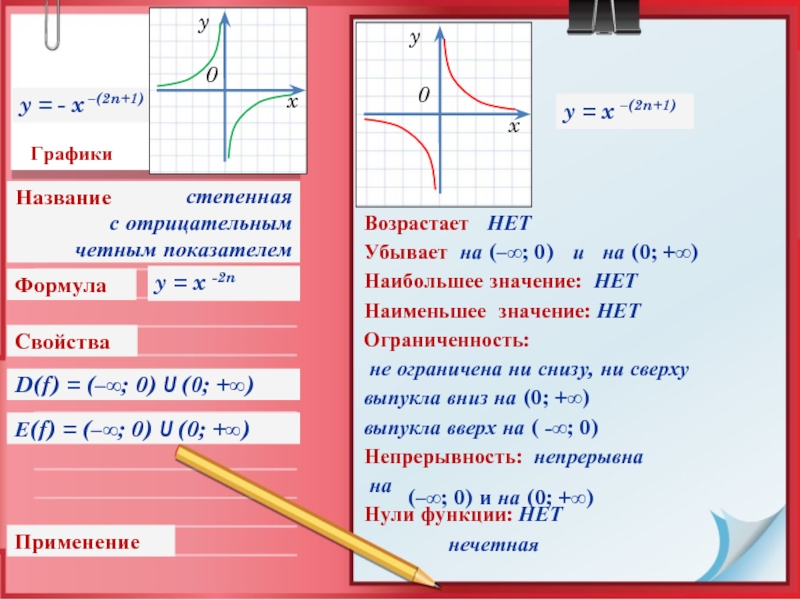
Слайд 15Графики
Свойства
Применение
Формула
Возрастает НЕТ
Убывает на (–∞; 0) и на
(0; +∞)
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
не ограничена ни снизу, ни сверху
выпукла вниз на (0; +∞)
выпукла вверх на ( -∞; 0)
Непрерывность: непрерывна
на
Нули функции: НЕТ
нечетная
Наибольшее значение: НЕТ
Наименьшее значение: НЕТ
Ограниченность:
не ограничена ни снизу, ни сверху
выпукла вниз на (0; +∞)
выпукла вверх на ( -∞; 0)
Непрерывность: непрерывна
на
Нули функции: НЕТ
нечетная
y = x -2n
y = x –(2n+1)
степенная
с отрицательным
четным показателем
y = - x –(2n+1)
Название
D(f) = (–∞; 0) U (0; +∞)
(–∞; 0) и на (0; +∞)
Е(f) = (–∞; 0) U (0; +∞)
Слайд 17Применение функций в науках
и деятельности человека
Рассмотрите график зависимости
силы тока от напряжения. Сравните сопротивления.
В каком из случаев показание резистора будет наибольшим?
В каком из случаев показание резистора будет наибольшим?
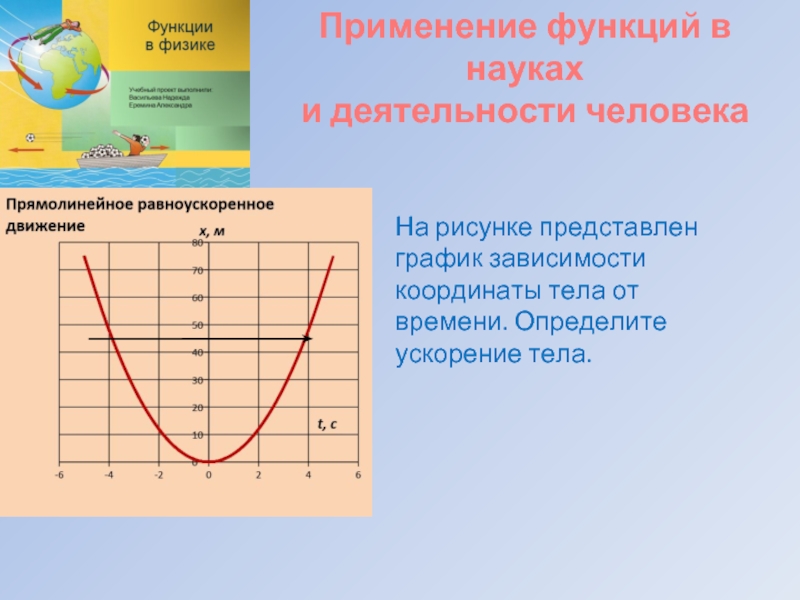
Слайд 18Применение функций в науках
и деятельности человека
На рисунке представлен
график зависимости координаты тела от времени. Определите ускорение тела.
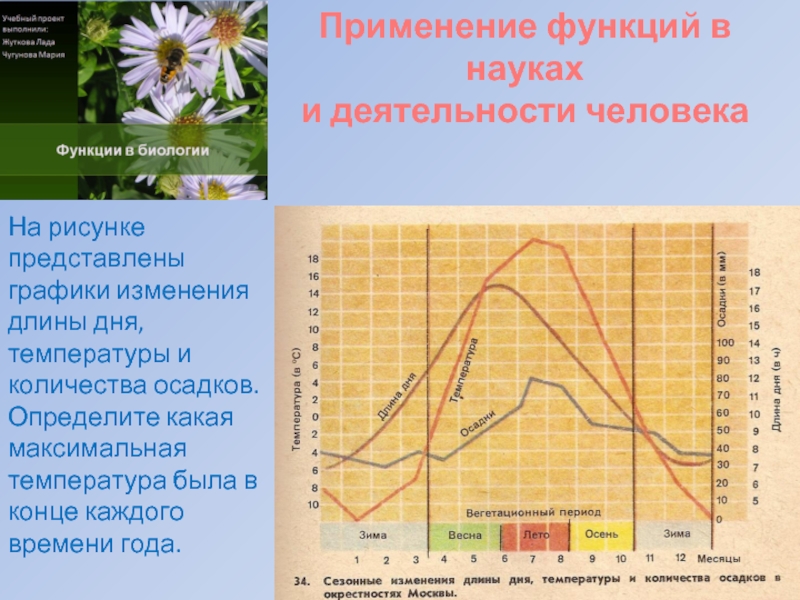
Слайд 19Применение функций в науках
и деятельности человека
На рисунке представлены
графики изменения длины дня, температуры и количества осадков. Определите какая максимальная температура была в конце каждого времени года.
Слайд 20 Домашнее задание
Алгебра 9
выполнить тест ( другой вариант);
найти
и решить задания о функциях в материалах ГИА (3 задания);
нарисовать с помощью функций рисунки в программе Excel;
подготовить вопросы о затруднениях в решении заданий к уроку – консультации
нарисовать с помощью функций рисунки в программе Excel;
подготовить вопросы о затруднениях в решении заданий к уроку – консультации
