- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение иррациональных уравнений презентация
Содержание
- 1. Решение иррациональных уравнений
- 2. Содержание Эпиграф.
- 3. Именно математика дает надежнейшие
- 4. Виды уравнений Целые уравнения Дробно-рациональные Иррациональные Тригонометрические Показательные Логарифмические
- 5. Определение Иррациональное уравнение – уравнение, содержащее
- 6. Какие из данных уравнений являются иррациональными? 1. 2. 3. 4.
- 7. Работаем устно
- 8. Методы решения Графический Основные алгебраические Переход
- 9. Графический метод (пример 1) Решите графически уравнение
- 10. Функционально-графический метод Пример: решите уравнение f(x)= g(x)=5-x,
- 11. Решите уравнения (алгоритм 2) (алгоритм 1) ((алгоритм)
- 12. Алгоритм 1 При n – четном Уедини
- 13. Алгоритм 2 При n - нечетном
- 14. Возведение в степень Решение. Возведем обе
- 15. Возведение в степень Решение.
- 16. Переход к равносильной системе Определить условия
- 17. Переход к равносильной системе
- 18. Специальные методы решения Метод пристального взгляда Найди
- 19. Область определения уравнения (ОДЗ) – это
- 20. Справка Корень n-й степени из а
- 21. Справка Модуль числа: |a| = a
- 22. Спасибо за урок! Успехов в изучении темы!
- 23. Об авторе Презентацию подготовила учитель математики
Слайд 2Содержание
Эпиграф.
Виды уравнений.
Определение иррациональных уравнений.
Упражнения на распознавание видов уравнений.
Работаем устно.
Методы решения.
Графический метод.
Функционально-графический метод.
Решите уравнения.
Возведение в степень (алгоритм 1).
Алгоритм 2.
Пример по алгоритму 1.
Пример по алгоритму 2.
Специальные методы решения уравнений.
Справка по ОДЗ.
Справка. Корень n-й степени.
Справка. Модуль.
Об авторе.
Слайд 3 Именно математика
дает надежнейшие правила:
кто им следует – тому
Л. Эйлер
Слайд 4Виды уравнений
Целые уравнения
Дробно-рациональные
Иррациональные
Тригонометрические
Показательные
Логарифмические
Слайд 5Определение
Иррациональное уравнение –
уравнение, содержащее
переменную под знаком
корня (радикала).
(примеры)
(справка)
Слайд 8Методы решения
Графический
Основные алгебраические
Переход к равносильной системе
(подробнее)
Специальные
Возведение обеих частей уравнения
(подробнее)
(Функционально-
графический)
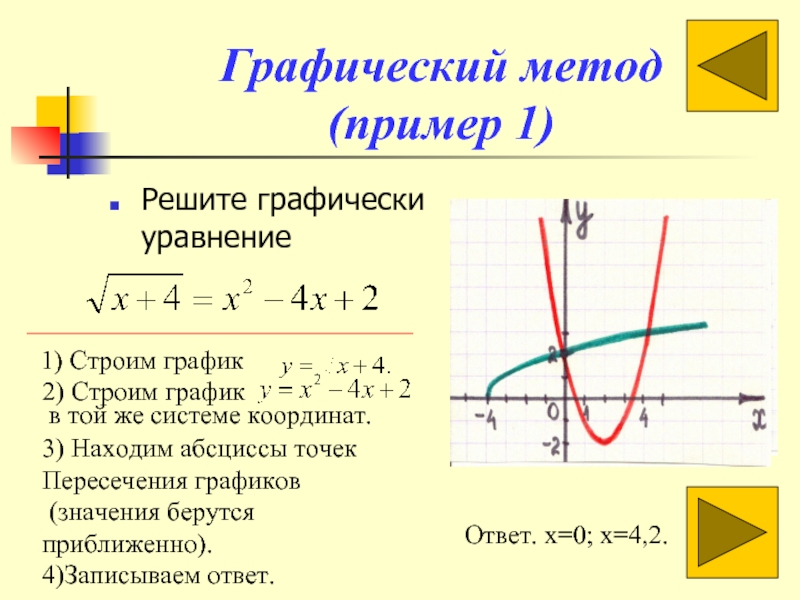
Слайд 9Графический метод
(пример 1)
Решите графически уравнение
Ответ. x=0; x=4,2.
1) Строим график
2) Строим
в той же системе координат.
3) Находим абсциссы точек
Пересечения графиков
(значения берутся приближенно).
4)Записываем ответ.
Слайд 10Функционально-графический
метод
Пример: решите уравнение
f(x)=
g(x)=5-x, убывает на D(g).
Уравнение f(x)=g(x) имеет не более одного
корня.
4.
Ответ. 2.
- возрастает на D(f).
Решение.
Слайд 12Алгоритм 1
При n – четном
Уедини корень (если необходимо);
Возведи обе части уравнения
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Выполни проверку!
Запиши ответ.
(к методам)
Слайд 13Алгоритм 2
При n - нечетном
Уедини корень (если необходимо);
Возведи обе части уравнения
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Запиши ответ.
(к методам)
Слайд 14Возведение в степень
Решение.
Возведем обе части уравнения в квадрат:
Преобразуем:
Проверка.
Если x=1, то в
0=0 (верно).
Если x=-2, то в левой части 3, в правой части -3,
3 не равно -3, значит, -2 не является корнем.
Ответ. 1.
*
Слайд 15Возведение в степень
Решение.
Возведем обе части уравнения
в 3-ю степень:
Преобразуем:
Ответ. 0 ;
*
Слайд 16Переход к равносильной
системе
Определить условия (если n –четно), при
которых обе
2. Возвести обе части уравнения в n-ю степень;
3. Составить систему из уравнения и неравенства;
4. Решить систему;
5. Записать ответ.
Определение.
Слайд 18Специальные методы решения
Метод пристального взгляда
Найди ОДЗ
Выполни замену
Умножай на сопряженное
Переходи к модулю
Оцени
(справка)
(справка)
(справка)
Слайд 19Область определения
уравнения (ОДЗ) –
это все значения переменной, при
которых данное
Замечание. Если ОДЗ уравнения есть
пустое множество, то говорят, что
данное уравнение не определено на
множестве R и решений заведомо быть
не может.