- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория узлов презентация
Содержание
- 1. Теория узлов
- 2. Исторический аспект
- 3. Узел В обычном смысле под узлом понимается
- 4. Изотропия узлов Если задан узел, то его
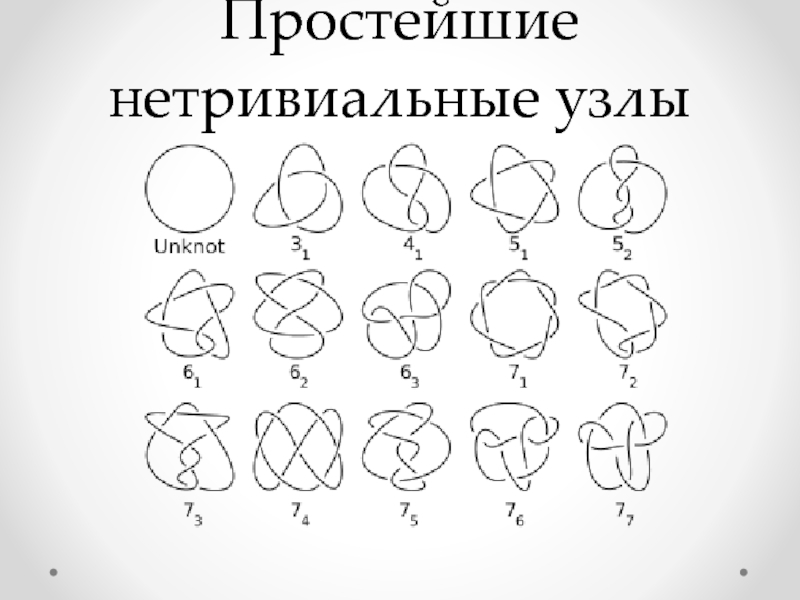
- 5. Простейшие нетривиальные узлы
- 6. Движения Рейдемейстера
- 7. Трёхцветные раскраски узлов Будем раскрашивать дуги в
- 8. Практика раскрасок Определите являются ли следующие узлы тривиальными?
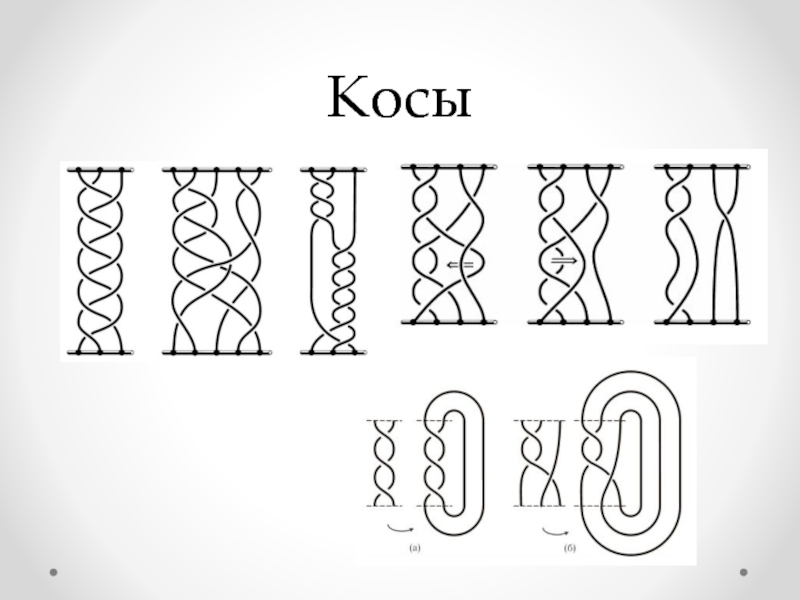
- 9. Косы
- 10. Математический объект: группа Непустое множество G с заданной на
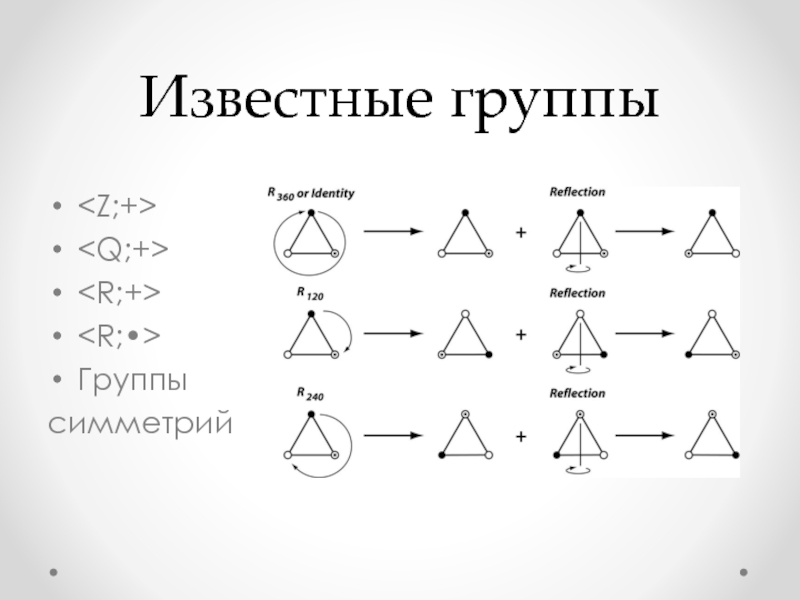
- 11. Известные группы Группы симметрий
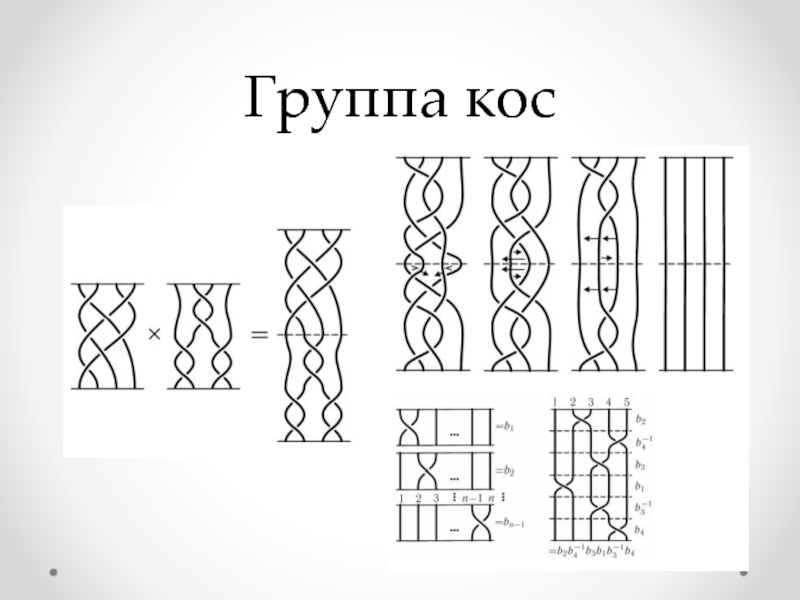
- 12. Группа кос
- 13. ПРАКТИКА ПЛЕТЕНИЯ УЗЛОВ
- 14. Прямой узел (+) — узел легко вяжется;
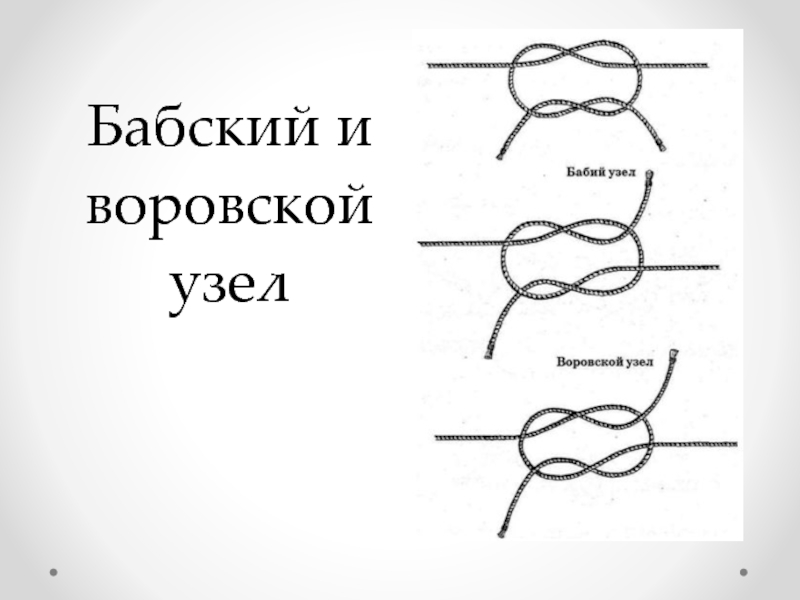
- 15. Бабский и воровской узел
- 16. Узел «Проводник» и «Заячьи ушки» Узел «проводник»
- 17. Узел «Восьмёрка» Узел «встречная восьмерка» (!) —
- 18. Беседочный узел Беседочный узел («булинь») (+) —
- 19. Теория узлов Лектор: Влада Сергеевна Бурмак
Слайд 3Узел
В обычном смысле под узлом понимается отрезок веревки, расположенный в трехмерном
Слайд 4Изотропия узлов
Если задан узел, то его можно шевелить (производить изотопию), двигая
Возникает естественный вопрос (главный в теории узлов): как по двум заданным узлам понять, изотопны они или нет. Иными словами, можно ли из одиного узла без разрезов и склейки получить другой.
Частным случаем является вопрос о распознавании тривиальности того или иного узла то есть о том, является ли заданный узел изотопным тривиальному узлу (то есть можно ли его развязать).
Слайд 7Трёхцветные раскраски узлов
Будем раскрашивать дуги в три цвета таким образом, чтобы
Количество правильных раскрасок диаграммы зацепления назовем значением функции раскрасок на данной диаграмме зацепления.
Слайд 10Математический объект: группа
Непустое множество G с заданной на нём бинарной операцией ⊕ называется группой
замкнутость
если a,b∈G и a⊕b=c, где c∈G
ассоциативность
a⊕(b⊕c)=(a⊕b)⊕c, где a,b,c∈G;
наличие нейтрального элемента e
для любого a∈G: a⊕e=e⊕a=a
наличие обратного элемента:
для любого a∈G, найдётся такой a-1∈G : a⊕ a-1 = a-1 ⊕a=e
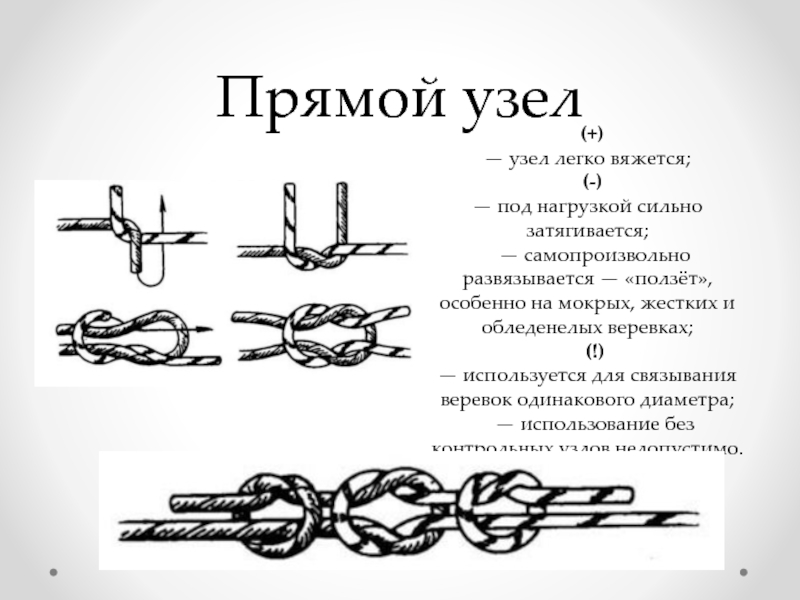
Слайд 14Прямой узел
(+)
— узел легко вяжется;
(-)
— под нагрузкой сильно затягивается;
— самопроизвольно развязывается —
(!)
— используется для связывания веревок одинакового диаметра; — использование без контрольных узлов недопустимо.
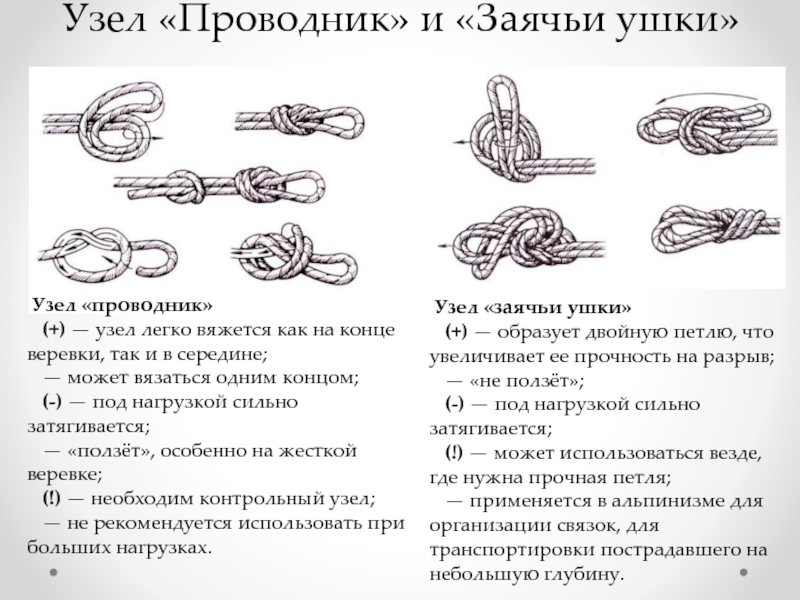
Слайд 16Узел «Проводник» и «Заячьи ушки»
Узел «проводник»
(+) — узел легко вяжется как на
Узел «заячьи ушки»
(+) — образует двойную петлю, что увеличивает ее прочность на разрыв;
— «не ползёт»;
(-) — под нагрузкой сильно затягивается;
(!) — может использоваться везде, где нужна прочная петля;
— применяется в альпинизме для организации связок, для транспортировки пострадавшего на небольшую глубину.
Слайд 17Узел «Восьмёрка»
Узел «встречная восьмерка»
(!) — надежный узел, хорошо держит;
— «не ползёт»;
(-) — вяжется
— сильно затягивается;
(!) — используется для связывания веревок как одинакового, так и разного диаметров.
Узел «восьмерка»
(+) — узел легко вяжется как на конце веревки, так и в середине;
— может вязаться одним концом;
— под нагрузкой сильно не затягивается;
— «не ползёт»;
(!) — удобен для образования надежной петли;
— применяется в альпинизме для организации связок и др.