- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проект. презентация
Содержание
- 1. Проект.
- 2. Ссылки. Смотреть по порядку Типы математики О
- 3. Законы… В основу пифагорейской теории музыки легли
- 4. Колебания. Частота колебаний определяет высоту звука.
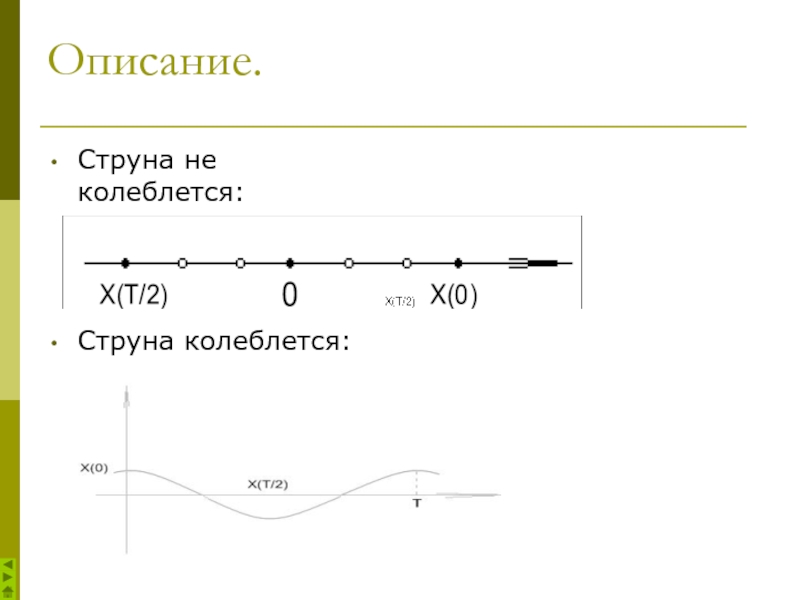
- 5. Описание. Струна не колеблется: Струна колеблется:
- 6. Колебания струны. Если колеблется протяженное тело (струна),
- 7. Таким образом… Итак, (по Пифагору) если первую
- 8. Темперация. Около 1700 года А. Веркмайстер осуществил
- 9. Продолжение. Для построения гаммы используются логарифмы
- 10. Ритм Ритм – основа музыкального движения, порядок
- 11. Такт, размер. |Во поле бе|рёза
- 12. Примеры составных размеров. Пример 1:
- 13. Полиритмия, полиметрия Полиритмия - в музыке —
- 14. Ритм в математике. В математику ритм проникает
- 15. Выявление МАТЕМАТИЧЕСКИХ ритмов Запишем натуральные числа в
- 16. Математические ритмы. Ритм в
- 17. Ритмы в триг. функциях
- 18. Упорядочивание.
- 20. В завершении данной темы… Итак, строгие математические
- 21. Список литературы. А.Г. Гейн, А.О. Касымов «Математика
Слайд 2Ссылки.
Смотреть по порядку
Типы математики
О Монохорде.
Смотреть законы
О колебаниях
Появление обертонов
Итог
Темперация
Ритм
Такт. Размер.
Математические ритмы
Упорядочивание
Текущее заключение
Список
Слайд 3Законы…
В основу пифагорейской теории музыки легли два закона:
Две струны дают консонанс,
Высота тона определяется частотой колебания струны ω, которая обратно пропорциональна длине струны l:
ω=α/ l
Слайд 4Колебания.
Частота колебаний определяет высоту звука.
1. 16 – 16000 Гц -
2. 16 – 5000 Гц – в музыке.
96/64 = 768/512 = 3/2 – КВИНТА.
Расстояние м/д нотами – интервал.
Обертоны – призвуки, которыми сопровождается основной звук.
Они слышны слабее и не мешают восприятию основного тона, но придают ему тембровую окраску.
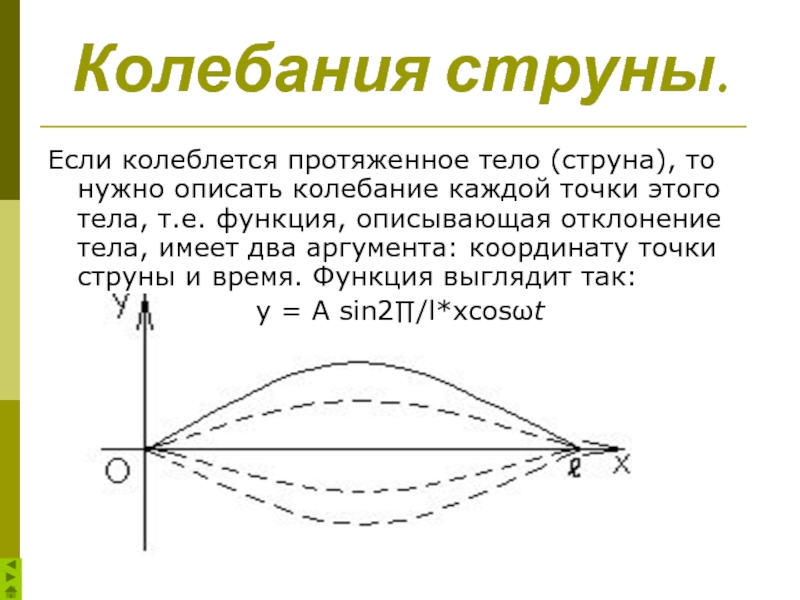
Слайд 6Колебания струны.
Если колеблется протяженное тело (струна), то нужно описать колебание каждой
y = A sin2∏/l*xcosωt
Слайд 7Таким образом…
Итак, (по Пифагору) если первую струну принять за основу, то
L2 : L3 = L4 : L1
Слайд 8Темперация.
Около 1700 года А. Веркмайстер осуществил гениальное решение: отказался от совершенных
Слайд 9Продолжение.
Для построения гаммы используются логарифмы соответствующих частот: log2w0, log2w1…log2wm.Октава (w0,
Геометрическая прогрессия w0,w1,…wm будет соответствовать арифметической log2w0,…
Музыкальная шкала разделена на 12 частей.
Слайд 10Ритм
Ритм – основа музыкального движения, порядок сочетания во времени всех элементов
В музыке – тактовый (акцентный) ритм, основанный на чередовании сильных и слабых долей.
Слайд 11
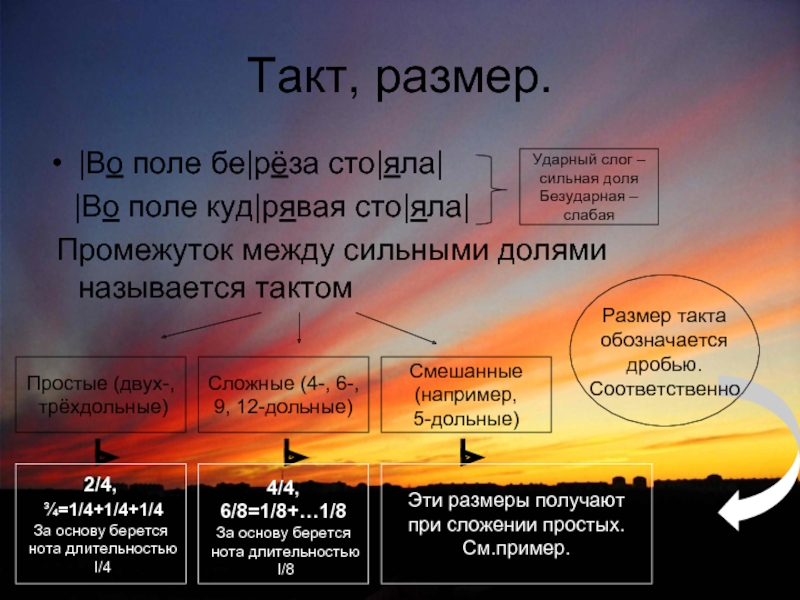
Такт, размер.
|Во поле бе|рёза сто|яла|
|Во поле куд|рявая сто|яла|
Промежуток
Ударный слог –
сильная доля
Безударная –
слабая
Простые (двух-,
трёхдольные)
Сложные (4-, 6-,
9, 12-дольные)
Смешанные
(например,
5-дольные)
Размер такта обозначается дробью. Соответственно
Эти размеры получают
при сложении простых.
См.пример.
4/4,
6/8=1/8+…1/8
За основу берется
нота длительностью
I/8
2/4,
¾=1/4+1/4+1/4
За основу берется
нота длительностью
I/4
Слайд 12Примеры составных размеров.
Пример 1:
Партитура Второго концерта для скрипки С.Прокофьева.
7/4=3/4+2/4+2/4
Пример 2:
Опера «Снегурочка» Н.Римского-Корсакова. Встречается размер: II/2
Слайд 13Полиритмия, полиметрия
Полиритмия - в музыке — одновременное сочетание двух или нескольких
Полиметрия - одновременное сочетание 2 или 3 метров, при котором не совпадают метрические акценты в разных голосах. Одна из форм организации полиритмии.
Пример 3: М.Глинка, опера «Иван Сусанин». (Сцена «Иван Сусанин и поляки», 3 действие):
Иван Сусанин поет в размере 2/4, а поляки – ¾.
Слайд 14Ритм в математике.
В математику ритм проникает как синоним слову закономерность. Например,
1/81=0,01234567912345679…, т.е.: 1/81=0,0(12345679). Закономерность – периодичность повторения (12345679).
1/3=0,(3)
1/7=0,(142857)
Примеры выявления числовых ритмов.
Слайд 15Выявление МАТЕМАТИЧЕСКИХ
ритмов
Запишем натуральные числа в виде т.н. Пифагорова Квадрата. Его особенность
Слайд 16Математические ритмы.
Ритм в расположении чисел, равных трём, выглядит так: 0
Слайд 20В завершении данной темы…
Итак, строгие математические методы построения музыкальных ладов не
Конечно же, роль математики в искусстве не ограничивается музыкой. Например, очень интересно построить математическую модель игры в теннис. Для просмотра этого раздела Вам необходимо активировать гиперссылку нажатием кнопки:
Слайд 21Список литературы.
А.Г. Гейн, А.О. Касымов «Математика и музыка»
Статья В.В. Липилиной из
А. И. Волошинов «Пифагор»
Математика и музыка: Методические указания для руководителей кружков НПОУ «Поиск»/Сост. И.А.Круглова; Под ред. В.Н. Сергеева. Омск: Омск. Ун-т, 1991, 90 с.
Садовский Л.Е., Садовский А.Л. Математика и спорт. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 192 с. – (Библиотечка «Квант». Вып. 44).
Ресурсы Интернета.