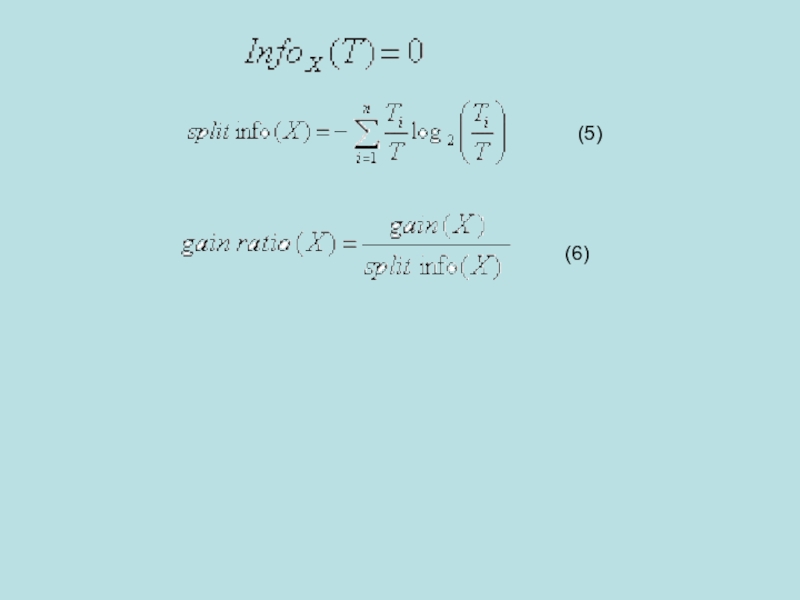ДЕРЕВЬЯ РЕШЕНИЙ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДЕРЕВЬЯ РЕШЕНИЙ презентация
Содержание
- 1. ДЕРЕВЬЯ РЕШЕНИЙ
- 2. Описание данных: Деревья решений позволяют хранить
- 3. 3. Множество T содержит примеры, относящиеся к
- 4. ДЕРЕВЬЯ РЕШЕНИЙ (CART) Описание атрибутов.
- 5. Пусть freq(Cj, S) – количество примеров из некоторого
- 6. (4) Критерий для выбора атрибута Пусть
- 7. 1.Выбираю точку разрыва = (67,50+68,00)/2=67,75 2. Ищу
- 8. GAIN (X)=0,299-0,199=0,1 Далее такой же подход ко
- 9. (5) (6)
- 10. Пусть T – множество обучающих примеров и X –
- 11. Пусть теперь проверка X с выходными значениями
Слайд 1Деревья решений – это способ представления правил в иерархической, последовательной структуре, где
Слайд 2
Описание данных: Деревья решений позволяют хранить информацию о данных в компактной
Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.
Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования(предсказания значений целевой переменной).
Пусть через {C1, C2, … Ck} обозначены классы (значения метки класса), тогда существуют 3 ситуации:
1. Множество T содержит один или более примеров, относящихся к одному классу Ck. Тогда дерево решений для Т – это лист, определяющий класс Ck;
2. Множество T не содержит ни одного примера, т.е. пустое множество. Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества отличного от T, скажем, из множества, ассоциированного с родителем;
Слайд 33. Множество T содержит примеры, относящиеся к разным классам. В этом
АЛГОРИТМЫ деревьев решений CART, C4.5, NewId, ITrule, CHAID, CN2 CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.
Слайд 4ДЕРЕВЬЯ РЕШЕНИЙ (CART)
Описание атрибутов.
Определенные классы. Каждый пример должен быть ассоциирован
3. Дискретные классы. Классы должны быть дискретными, т.е. иметь конечное число значений.
- Пусть нам задано множество примеров T, где каждый элемент этого множества описывается m атрибутами.
Количество примеров в множестве T будем называть мощностью этого множества и будем обозначать |T|.
Пусть метка класса принимает следующие значения C1, C2 … Ck.
- Пусть мы имеем проверку X, которая принимает n значений A1, A2 … An.
Тогда разбиение T по проверке X даст нам подмножества T1, T2 … Tn, при X равном соответственно A1, A2 … An.
Слайд 5Пусть freq(Cj, S) – количество примеров из некоторого множества S, относящихся к
(1)
(2)
(3)
Слайд 6(4)
Критерий для выбора атрибута
Пусть числовой атрибут имеет конечное число значений.
Обозначим их {v1, v2 … vn}.
{v1, v2 … vi}, {vi+1, vi+2 … vn}.
ПОРОГ
GAIN (X)=Info (T)- InfoX (T)
Слайд 71.Выбираю точку разрыва
= (67,50+68,00)/2=67,75
2. Ищу
= - [[(19/37)*log(19/37)]+[(18/37)*log(18/37)]]=0.299
3. Ищем
InfoX(T)= [|T1|\|T|*info(T1)]+[|T2\|T|*info(T2)|]
Info(T1)=
=0.274
Info(T2)= 0
InfoX(T)= [27\37*0.274]+ 10\37*0 = 0.199
4. Критерий
GAIN (X)=Info (T)- InfoX (T)
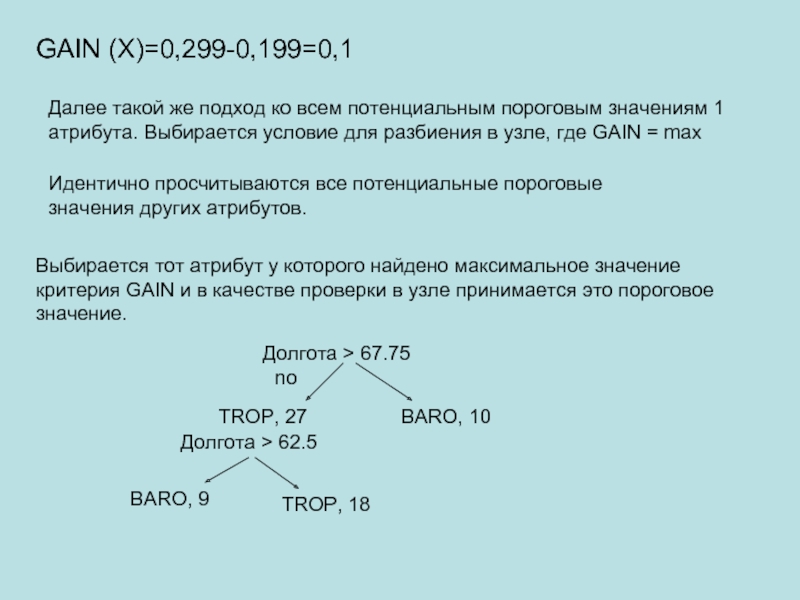
Слайд 8GAIN (X)=0,299-0,199=0,1
Далее такой же подход ко всем потенциальным пороговым значениям 1
Идентично просчитываются все потенциальные пороговые значения других атрибутов.
Выбирается тот атрибут у которого найдено максимальное значение критерия GAIN и в качестве проверки в узле принимается это пороговое значение.
Долгота > 67.75
TROP, 27
BARO, 10
no
Долгота > 62.5
BARO, 9
TROP, 18
Слайд 10Пусть T – множество обучающих примеров и X – проверка по некоторому атрибуту
(7)
(8)
(9)
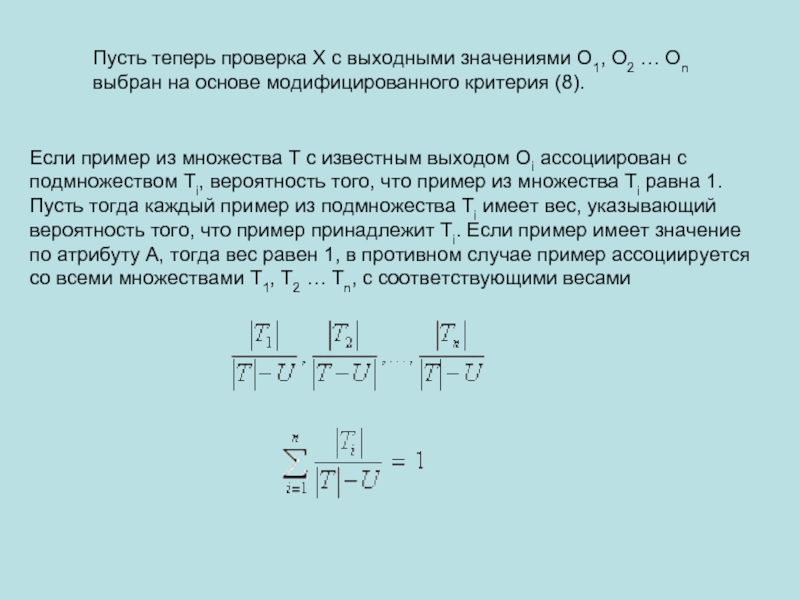
Слайд 11Пусть теперь проверка X с выходными значениями O1, O2 … On
Если пример из множества T с известным выходом Oi ассоциирован с подмножеством Ti, вероятность того, что пример из множества Ti равна 1. Пусть тогда каждый пример из подмножества Ti имеет вес, указывающий вероятность того, что пример принадлежит Ti. Если пример имеет значение по атрибуту A, тогда вес равен 1, в противном случае пример ассоциируется со всеми множествами T1, T2 … Tn, с соответствующими весами






![1.Выбираю точку разрыва= (67,50+68,00)/2=67,752. Ищу = - [[(19/37)*log(19/37)]+[(18/37)*log(18/37)]]=0.2993. Ищем InfoX(T)= [|T1|\|T|*info(T1)]+[|T2\|T|*info(T2)|]Info(T1)= - [[ 9\27 *](/img/tmb/1/54070/977be007a5631dc6e5b99c4927329c43-800x.jpg)