- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок – игра Редакция презентация
Содержание
- 1. Урок – игра Редакция
- 2. Виды функций у = kx +
- 3. Газета «Математический вестник» выпуск №2 В мире функций
- 4. План работы: Планерка:
- 5. ПРОИЗВОДСТВЕННОЕ СОВЕЩАНИЕ отдел писем информационный отдел
- 6. Домашнее задание Составить контрольную работу по теме
- 7. Отдел писем Письмо почтальона Печкина Письмо Незнайки Заказное письмо профессора Цифиркина Производственное совещание
- 8. Здравствуйте, дорогая редакция.
- 9. п р о п
- 10. Письмо Незнайки Здравствуйте, редакция газеты «Математический вестник».
- 11. Задание: установите соответствие: А. у =
- 12. В отдел писем
- 13. Заказное письмо из лаборатории профессора Цифиркина При
- 14. х у -3 0 1 у= -3х
- 15. Информационный отдел Задание 1 Задание 2 Производственное совещание
- 16. Задание № 1 Мы используем различные способы
- 17. Задание № 2 На рисунке функции представлены
- 18. Производственное совещание у = 3х
- 19. Проблемный отдел Проблема № 1 Проблема № 2 Проблема № 3 Производственное совещание
- 20. Проблема № 1 Наш специальный корреспондент сообщил,
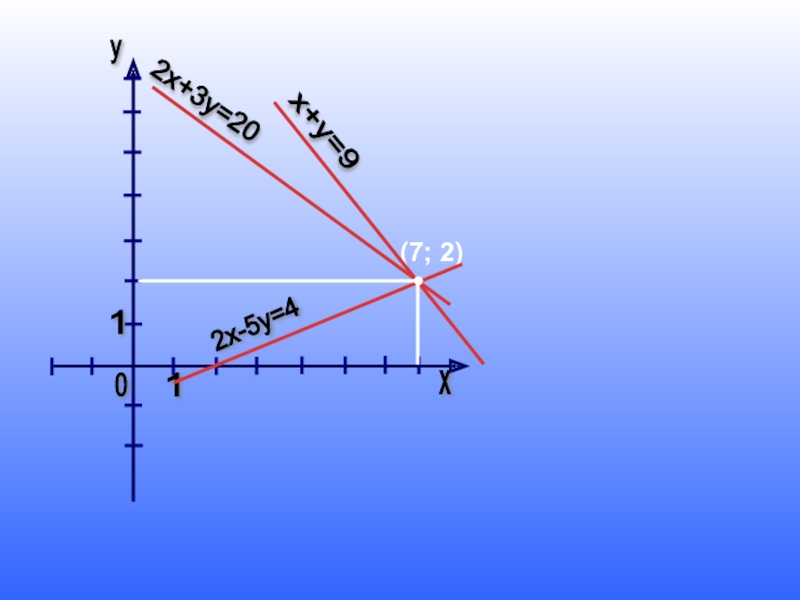
- 21. 1 1 0 у х (7; 2) 2х+3у=20 х+у=9 2х-5у=4
- 22. Некто построил график линейного уравнения, но забыл
- 23. Решение: m = 12, тогда уравнение
- 24. Проблема № 3 Один читатель прислал в
- 25. х у 1 1 0
- 26. Отдел развлечений Найден древний папирус, который представляет
- 27. 1. у = х + 2 ,
- 28. х у 1 1 0 х у 0 Это интересно
- 29. Некоторые специалисты считают, что кошку одомашнили
- 30. Отдел расследований Подготовка к расследованию: Говорят, что
- 31. Частное расследование Проведите частное расследование по следующим
- 32. х у 1 1 х у 0
- 33. х у 1 1 х у 0
- 34. х у 1 1 х у 0
- 35. Спасибо за урок
Слайд 4
План работы:
Планерка:
Работа в отделах: 1350 -1425
3. Обеденный перерыв: 1425 – 1435
4. Производственное совещание: 1435 – 1500
5. Премии 1500– 1505
6. Командировка 1505 – 1515
Слайд 5ПРОИЗВОДСТВЕННОЕ СОВЕЩАНИЕ
отдел писем
информационный отдел
проблемный отдел
отдел развлечений
отдел расследований
домашнее задание
Слайд 6Домашнее задание
Составить контрольную работу по теме «Функции», состоящую из 4 заданий:
Задания
1. Умение решать уравнения графическим способом.
2. Умение находить наибольшее и наименьшее значение функции.
3. Умение строить графики кусочных функций.
4. Умение находить значения функции у = f(x) при заданном значении аргумента
Оформить на отдельных листах.
Слайд 7Отдел писем
Письмо почтальона Печкина
Письмо Незнайки
Заказное письмо профессора Цифиркина
Производственное совещание
Слайд 8
Здравствуйте, дорогая редакция. Недавно в одной газете на глаза мне попался
С уважением почтальон Печкин
P.S. Шарик и кот Матроскин присоединяются к моей просьбе.
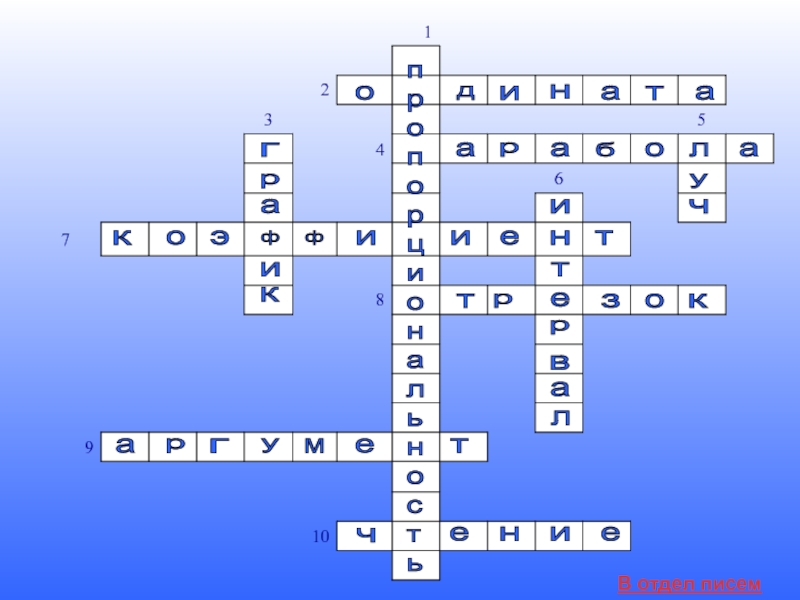
Слайд 9п р о п о р ц и о н а
о
д
и
н
а
т
а
а
а
а
о
р
б
л
г
р
а
ф
и
к
у
ч
и
н
т
е
р
в
а
л
к
о
э
ф
и
и
е
т
т
р
з
о
к
а
р
г
у
м
е
т
ч
е
н
и
е
В отдел писем
Слайд 10Письмо Незнайки
Здравствуйте, редакция газеты «Математический вестник». Пишет вам верный читатель Низнайка.
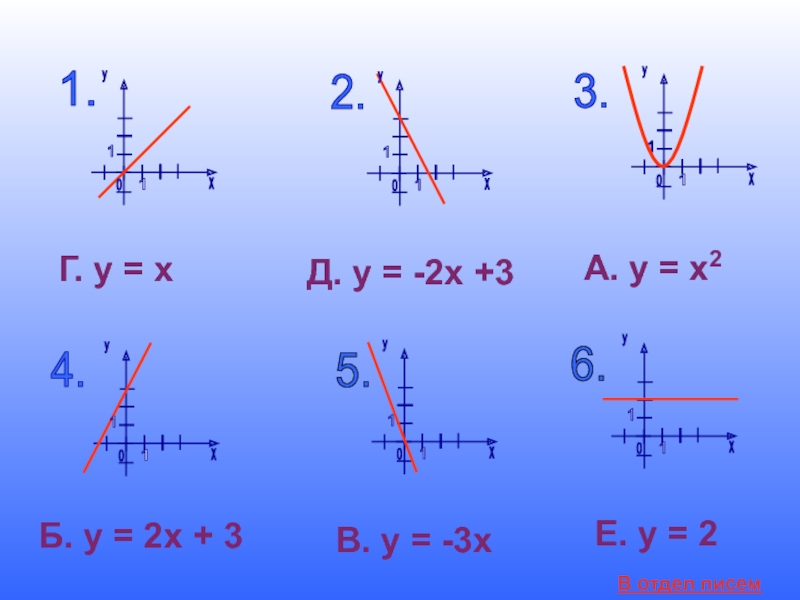
Слайд 11Задание: установите соответствие:
А. у = х2 В. у = -3х Д. у
Б. у = 2х + 3 Г. у = х Е. у = 2
3.
Слайд 13Заказное письмо из лаборатории профессора Цифиркина
При решении сверхсекретной задачи получилось уравнение
Заранее благодарен, профессор Цифиркин.
В отдел писем
Производственное совещание
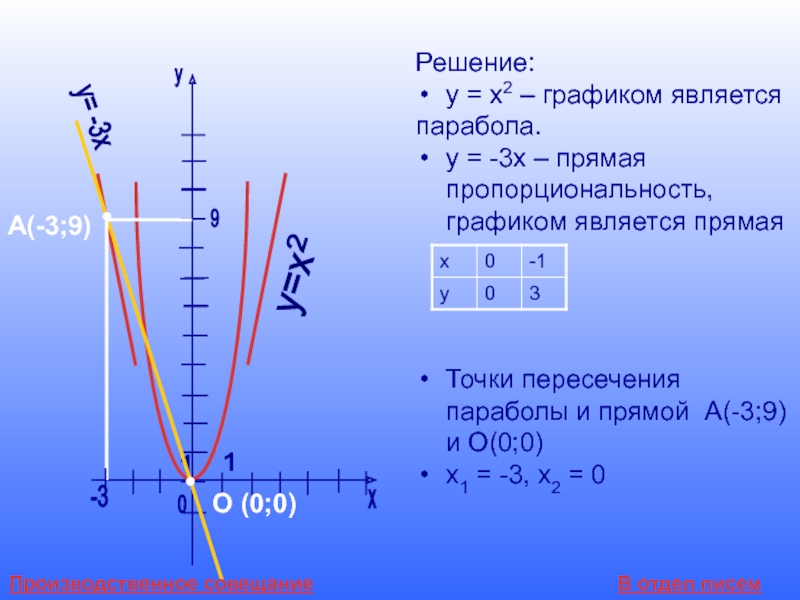
Слайд 14х
у
-3
0
1
у= -3х
А(-3;9)
О (0;0)
Решение:
у = х2 – графиком является
парабола.
у =
Точки пересечения параболы и прямой А(-3;9) и О(0;0)
х1 = -3, х2 = 0
9
1
Производственное совещание
В отдел писем
Слайд 16Задание № 1
Мы используем различные способы записи функции: аналитический, графический, табличный.
Слайд 17Задание № 2
На рисунке функции представлены различными способами.
Какие это способы?
Все ли они вам известны.
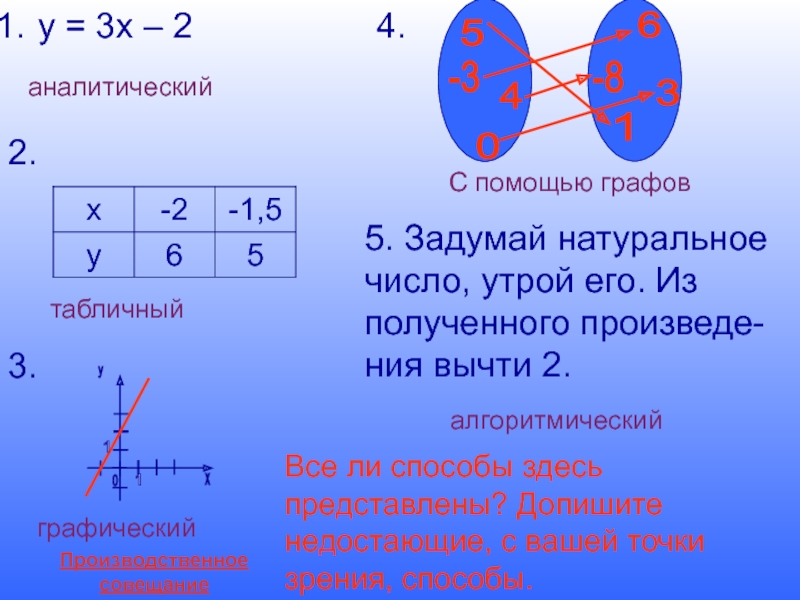
Слайд 18Производственное совещание
у = 3х – 2
2.
3.
4.
5. Задумай натуральное
число, утрой
полученного произведе-
ния вычти 2.
аналитический
табличный
графический
С помощью графов
алгоритмический
Все ли способы здесь представлены? Допишите недостающие, с вашей точки зрения, способы.
Слайд 20Проблема № 1
Наш специальный корреспондент сообщил, что обнаружил три линейных уравнения
2х + 3у = 20
х + у = 9
2х – 5у = 4
Говорят, что у этих уравнений есть что-то общее. Что общее у данных уравнений?
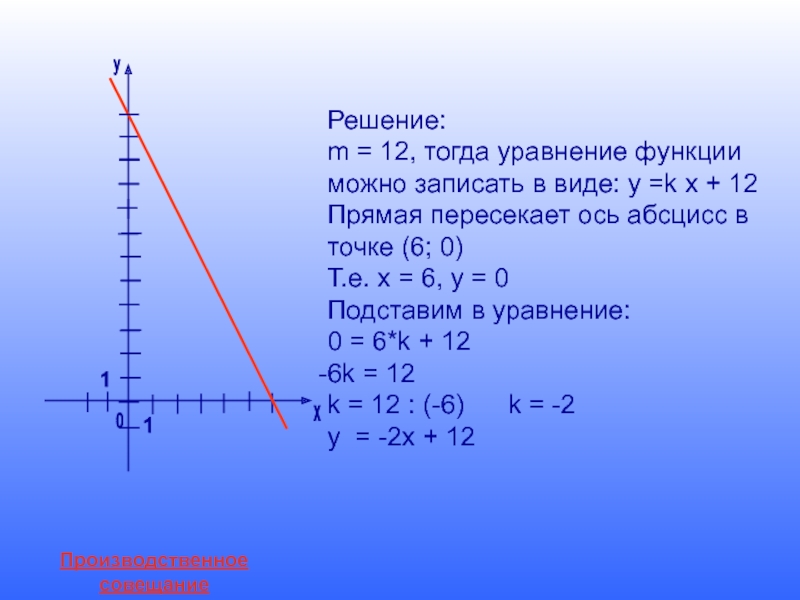
Слайд 22Некто построил график линейного уравнения, но забыл его аналитическую запись. Помогите
Проблема № 2
Производственное совещание
Слайд 23Решение:
m = 12, тогда уравнение функции
можно записать в виде:
Прямая пересекает ось абсцисс в
точке (6; 0)
Т.е. х = 6, у = 0
Подставим в уравнение:
0 = 6*k + 12
6k = 12
k = 12 : (-6) k = -2
у = -2х + 12
Производственное совещание
Слайд 24Проблема № 3
Один читатель прислал в редакцию рисунок и таблицу, которую
Разберитесь, что это за таблица.
Что она описывает?
Как ее заполнить?
Производственное совещание
Слайд 25х
у
1
1
0
х ϵ [-1; 6]
x = 0
x ϵ (0; 6]
x
11
-1
x ϵ [-1; 3)
нет
х=3
Производственное совещание
Слайд 26Отдел развлечений
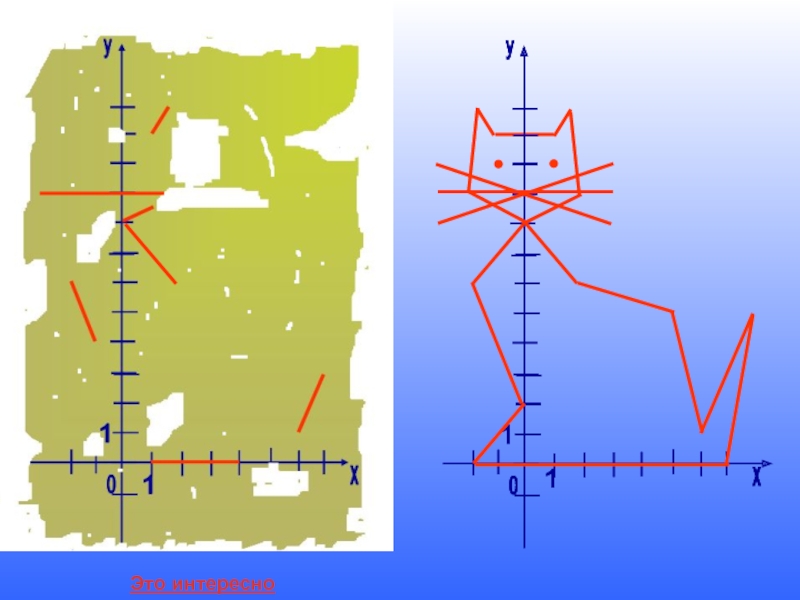
Найден древний папирус, который представляет собой очень важную историческую ценность.
Кто изображен на рисунке?
Как вы думаете, в какой стране мог быть найден такой папирус? Почему?
Слайд 271. у = х + 2 , -2
2. у = -2х + 2 , -2 ≤ х < 0
3. у = х + 8, -2 < х ≤ 0
4. у = -0,5х + 8 , -2 ≤ х < 0
5. у = 6х + 21, -2 < х ≤ -1,5
6. у = -2х + 9, -1,5 < х ≤ -1
7. у = 11, -1 < х ≤ 1
8. у = 2х + 9, 1 < х ≤ 1,5
19. у= -6х + 21, 1,5 < х ≤ 2
10. у = 0,5х + 8 , 0 < х < 2
11. y = -x + 8, 0 < х ≤ 2
12. , 2 < х ≤ 5
13. у = -4х + 25, 5 < х ≤ 6
14. у = 2х – 11, 6 < х ≤ 8
15. у = 5х – 35, 7 ≤ х < 8
16. у = 0, -2 ≤ х ≤ 7
17. , -3 ≤ х ≤ 3
18. , -3 ≤ х ≤ 3
20. у = 9, -3 ≤ х ≤ 3
Глаза: (-1; 10), (1; 10)
1. у = х + 2 , -2 ≤ х ≤ 0
2. у = -2х + 2 , -2 ≤ х < 0
3. у = х + 8, -2 < х ≤ 0
4. у = -0,5х + 8 , -2 ≤ х < 0
5. у = 6х + 21, -2 < х ≤ -1,5
6. у = -2х + 9, -1,5 < х ≤ -1
7. у = 11, -1 < х ≤ 1
8. у = 2х + 9, 1 < х ≤ 1,5
19. у= -6х + 21, 1,5 < х ≤ 2
10. у = 0,5х + 8 , 0 < х < 2
11. y = -x + 8, 0 < х ≤ 2
12. , 2 < х ≤ 5
13. у = -4х + 25, 5 < х ≤ 6
14. у = 2х – 11, 6 < х ≤ 8
15. у = 5х – 35, 7 ≤ х < 8
16. у = 0, -2 ≤ х ≤ 7
17. , -3 ≤ х ≤ 3
18. , -3 ≤ х ≤ 3
20. у = 9, -3 ≤ х ≤ 3
Глаза: (-1; 10), (1; 10)
Слайд 29Некоторые специалисты считают, что кошку
одомашнили в Нубии (историческая область
в
Оттуда кошки попали в Египет, где считались
священными животными. Богиню плодородия
Бастет египтяне изображали в виде кошки или
женщины с кошачьей головой. Кошки жили в
каждом доме. Им уступали дорогу, а во время
пожара первыми выносили из дома. Когда
пушистая любимица умирала, все члены
семьи в знак скорби сбривали брови.
Производственное совещание
Это интересно
Слайд 30Отдел расследований
Подготовка к расследованию:
Говорят, что графики линейных функций в координатной плоскости
Так ли это?
От чего зависит взаимное расположение двух прямых в координатной плоскости?
Проверьте, каково взаимное расположение графиков следующих линейных функций в координатной плоскости:
у = 3х +4 и у = -2х + 9
у = 6х + 2 и у = 6х – 13
у = -х – 1 и у = -1 – х
Слайд 31Частное расследование
Проведите частное расследование по следующим заданиям:
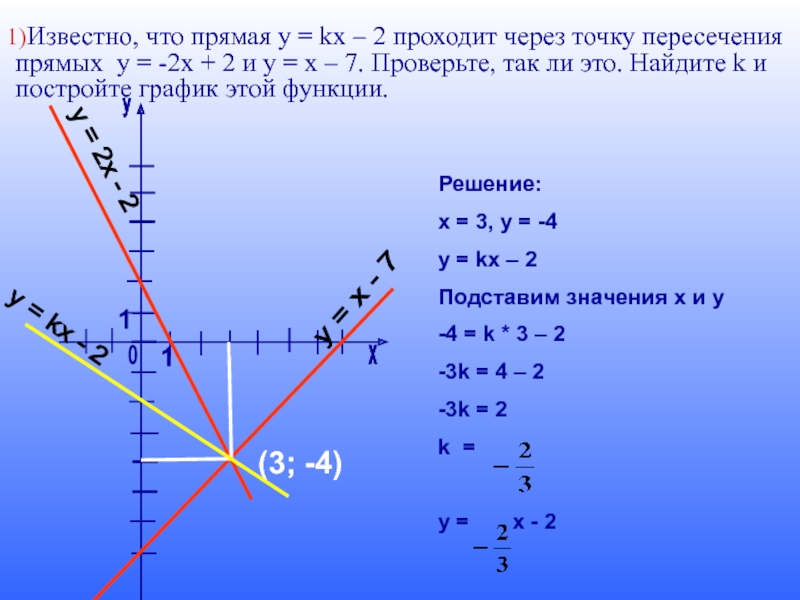
1) Известно, что прямая у
2) Как составить уравнение прямой, проходящей через точку пересечения прямых 4х – у = 7 и 3х + 2у = -3 и параллельно прямой у = 2х – 1.
3) Говорят, что прямые х + 2у = 3 и ах – 4у = 12 пересекаются в точке, принадлежащей оси абсцисс. При каком значении а это может произойти? Сделайте рисунок.
Производственное совещание
Слайд 32х
у
1
1
х
у
0
(3; -4)
Решение:
х = 3, у = -4
у = kх – 2
Подставим
-4 = k * 3 – 2
-3k = 4 – 2
-3k = 2
k =
y = x - 2
у = 2х - 2
у = х - 7
у = kх - 2
Известно, что прямая у = kх – 2 проходит через точку пересечения прямых у = -2х + 2 и у = х – 7. Проверьте, так ли это. Найдите k и постройте график этой функции.
Слайд 33х
у
1
1
х
у
0
3х-2у=-3
4х-у=7
у = 2х - 1
у = 2х - 5
(1; -3)
Решение:
Графики функций
у = 2х + m
х = 1, у = - 3
Подставим значения х и у
-3 = 2 * 1 + m
m = -3 – 2= -5
у = 2х - 5
2) Как составить уравнение прямой, проходящей через точку
пересечения прямых 4х – у = 7 и 3х + 2у = -3 и параллельно
прямой у = 2х – 1.
Слайд 34х
у
1
1
х
у
0
4х-у=7
х-у = 3
(3; 0)
Решение:
График функции 4х – у = 7 пересекает
х = 3, у = 0
Подставим значения х и у
в уравнение ах – 4у = 12:
а*3 – 4*0 = 12
3а = 12 или а = 4
Получим:
4х – 4у = 12 или х – у = 3
3) Говорят, что прямые х + 2у = 3 и ах – 4у = 12 пересекаются
в точке, принадлежащей оси абсцисс. При каком значении а
это может произойти? Сделайте рисунок.
Производственное совещание


















![ху110х ϵ [-1; 6] x = 0x ϵ (0; 6] x ϵ [-1; 0) 11-1x](/img/tmb/4/312945/f6f51d5405225ea0316f996308b05126-800x.jpg)