- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Путешествие во времени презентация
Содержание
- 1. Путешествие во времени
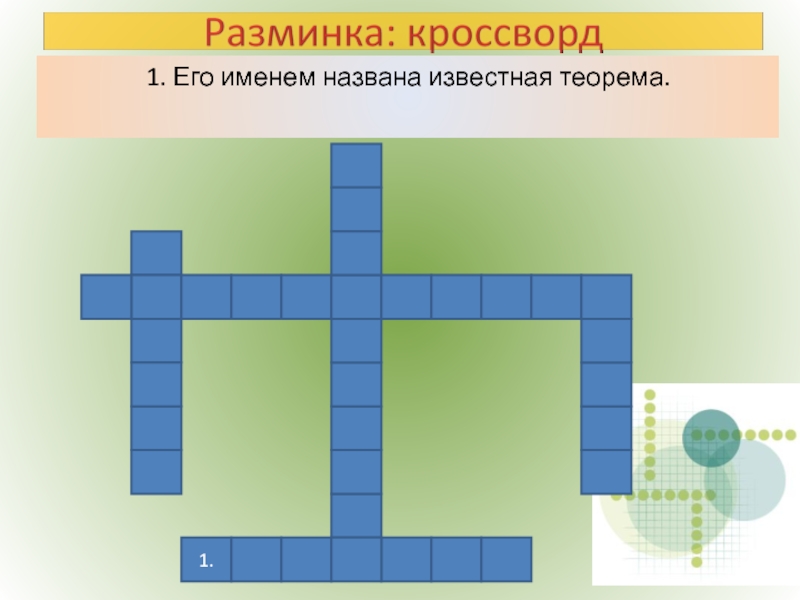
- 2. 1. Его именем названа известная теорема.
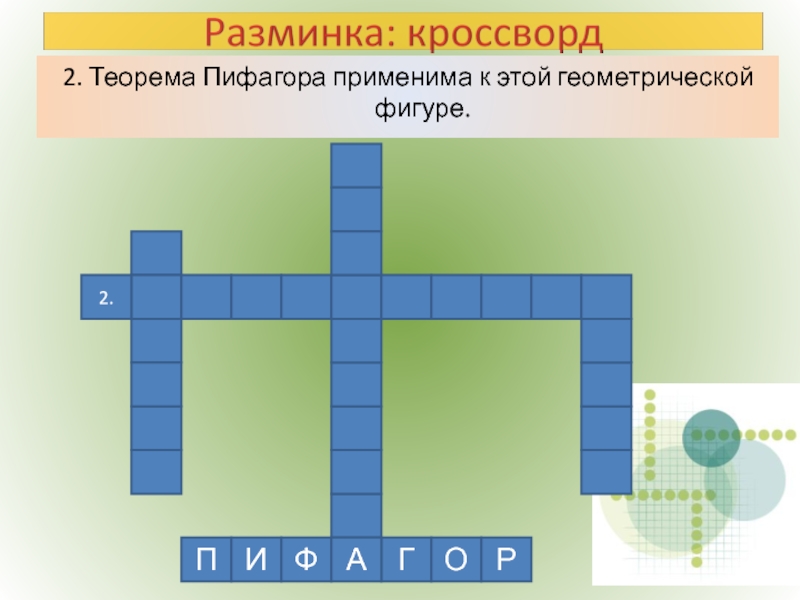
- 3. 2. Теорема Пифагора применима к этой геометрической
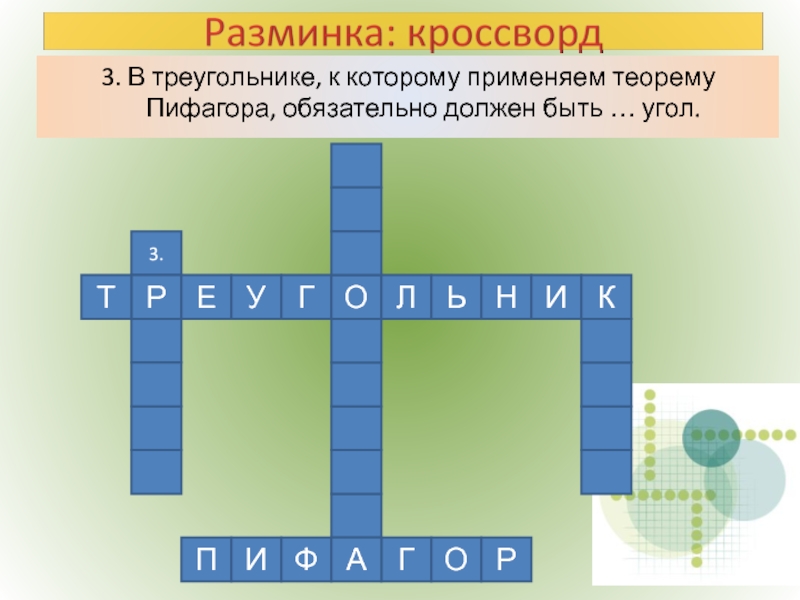
- 4. 3. В треугольнике, к которому применяем теорему
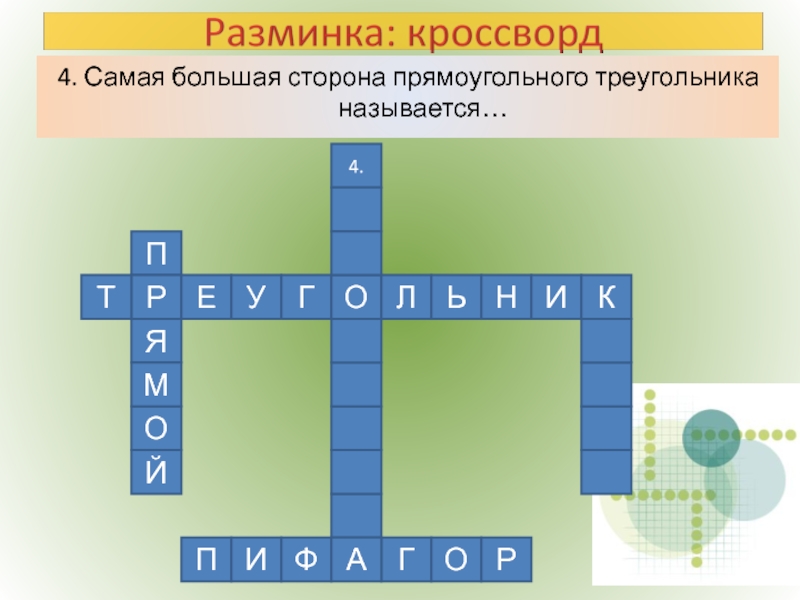
- 5. 4. Самая большая сторона прямоугольного треугольника называется…
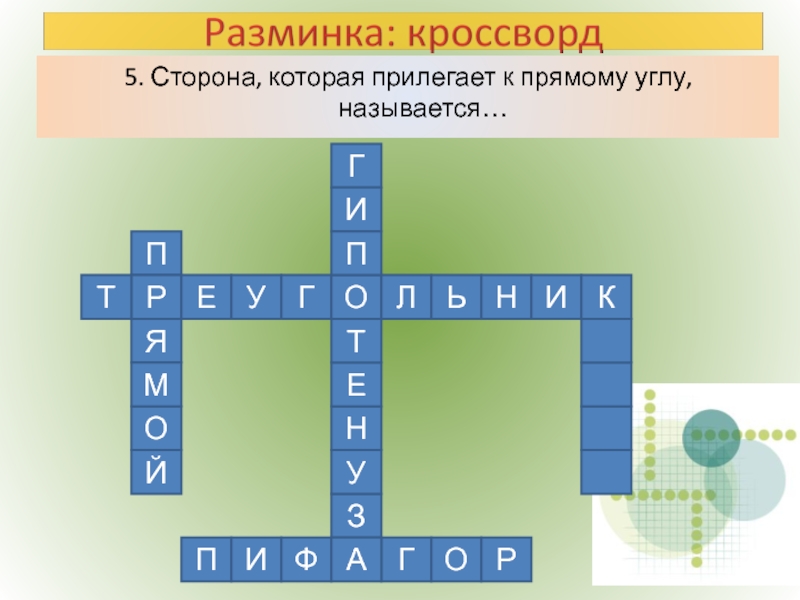
- 6. 5. Сторона, которая прилегает к прямому углу,
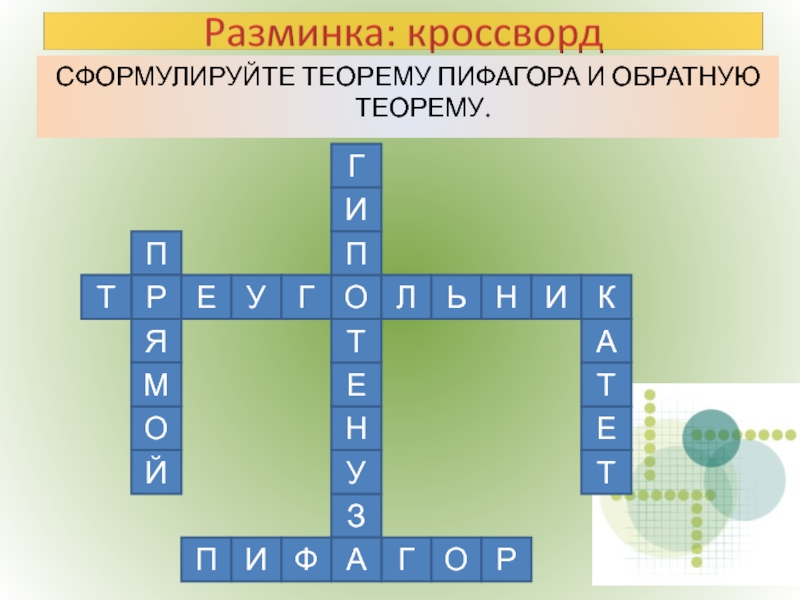
- 7. СФОРМУЛИРУЙТЕ ТЕОРЕМУ ПИФАГОРА И ОБРАТНУЮ ТЕОРЕМУ. П
- 8. Он родился в 580 г. до н.э.
- 9. Кротон... Здесь начинается самый славный период биографии
- 10. В знак протеста против тирана Поликрата, который
- 11. 1. Верно ли: катет больше гипотенузы?
- 12. 1. Верно ли: катет больше гипотенузы? –
- 13. Древняя индийская задача Над озером
- 14. Решение: Пусть глубина реки
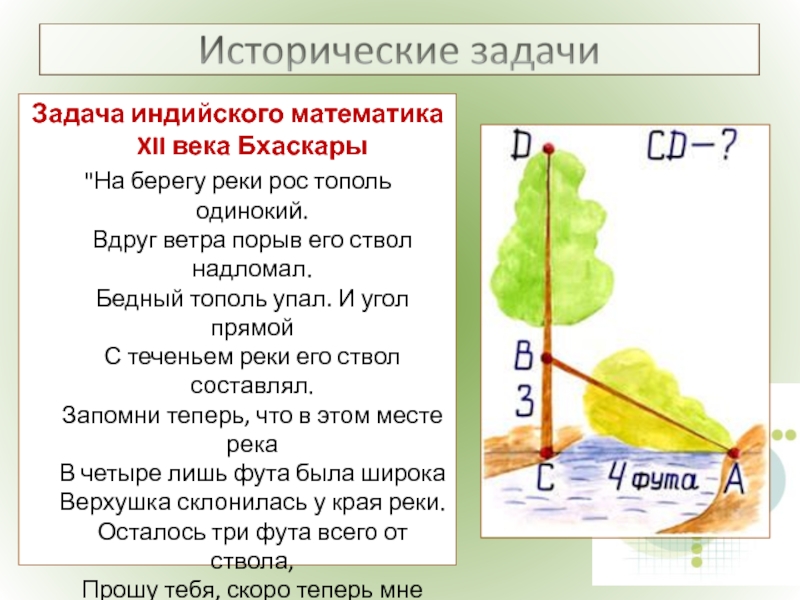
- 16. Задача индийского математика XII века Бхаскары
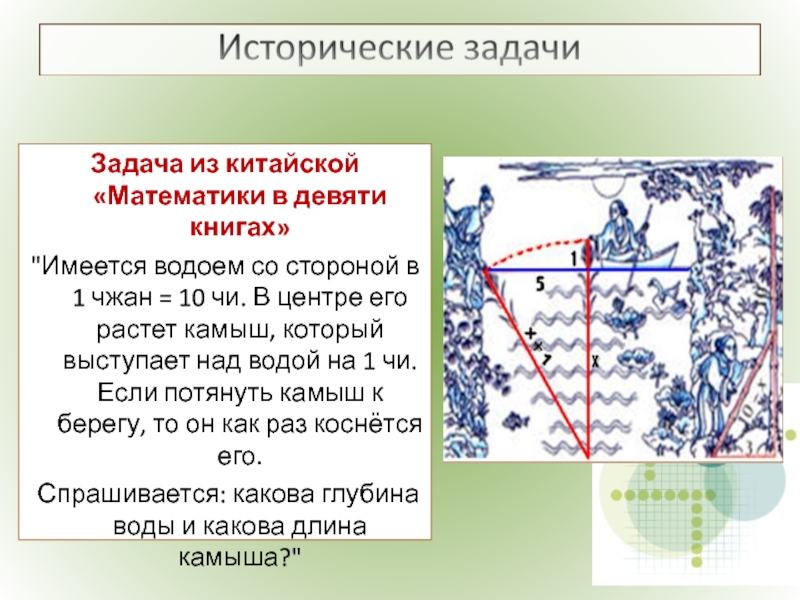
- 17. Задача из китайской «Математики в девяти
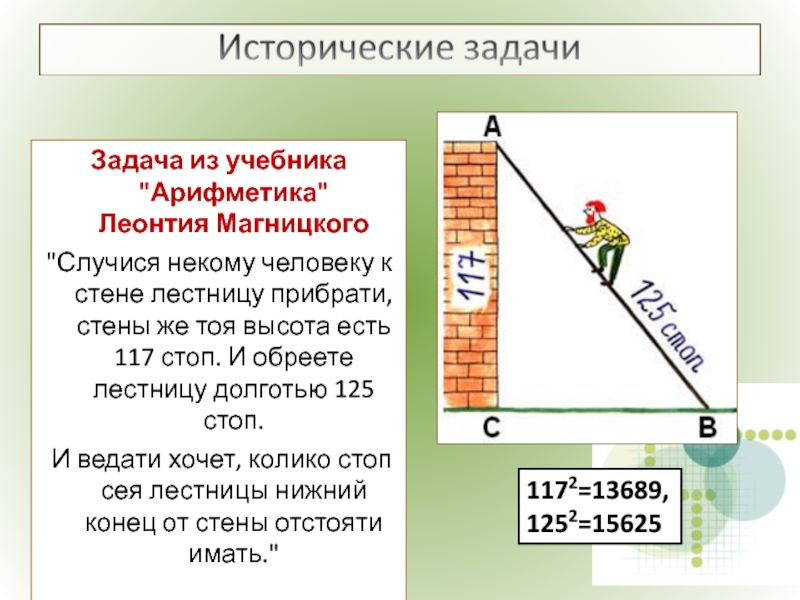
- 18. Задача из учебника "Арифметика" Леонтия Магницкого
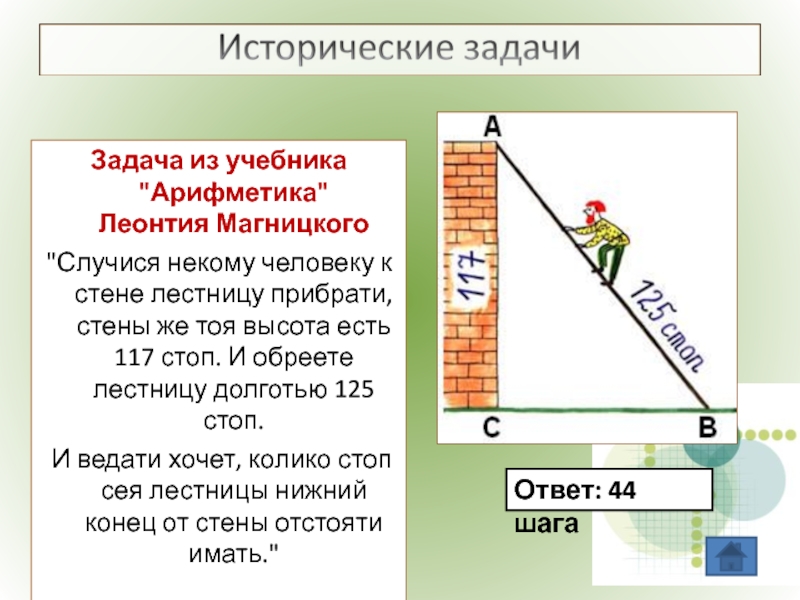
- 19. Задача из учебника "Арифметика" Леонтия Магницкого
- 21. Для крепления мачты нужно установить 4
- 22. Некоторые из 325 Пифагоровых заповедей: Мысль –
- 23. Пифагорейцы с равным усердием заботились и о
- 24. теорема о сумме внутренних углов треугольника; построение
- 26. Значение теоремы Пифагора Как символ вечного союза
- 27. О т е о р е м е П и ф а г о р а Суть истины вся в том,
- 28. http://www.zaitseva-irina.ru http://www.samos-travel.com/photos.html http://images.yandex.ru http://clck.yandex.ru/redir/AiuY0DBWFJ4ePaEse6rgeAjgs2pI3DW99KUdgowt9Xt0dmymRAsAFBPuMjsGwhcEy Остров Самос
Слайд 43. В треугольнике, к которому применяем теорему Пифагора, обязательно должен быть
3.
Р
Е
У
Г
О
Л
Ь
Н
И
Т
К
Г
П
И
Ф
А
О
Р
Слайд 8Он родился в 580 г. до н.э. в Древней Греции на
Юношей Пифагор перебрался в город Милеет и стал учеником Фалеса.
По совету учителя перебрался в Египет и продолжил обучение.
После продолжительного обучения по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов и 10 лет постигал науку Вавилона.
ПИФАГОР САМОССКИЙ
(ок. 580 – ок. 500 г. до н.э.)
Слайд 9Кротон... Здесь начинается самый славный период биографии Пифагора. В Кротоне Пифагор
Слайд 10В знак протеста против тирана Поликрата, который тогда правил островом Самос,
Там он организовал тайный союз молодёжи из представителей аристократии. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы занимались математикой, философией, естественными науками.
ПИФАГОР САМОССКИЙ
(ок. 580 – ок. 500 г. до н.э.)
Слайд 11 1. Верно ли: катет больше гипотенузы?
2. Могут ли быть в
3. Может ли быть в прямоугольном треугольнике 2 равных катета?
4. Найти AB=?
5. Является ли треугольник прямоугольным, если его стороны равны 6; 8; 10?
Слайд 121. Верно ли: катет больше гипотенузы? – Нет
2. Могут ли быть
3. Может ли быть в прямоугольном треугольнике 2 равных катета? – Да, если ∆ равнобедренный
4. Найти AB=? АВ2=АС2+ВС2
АВ2=42+32
АВ2=25
АВ=5 см –
как называют этот треугольник?
5. Является ли треугольник прямоугольным, если его стороны равны 6; 8; 10?
Да, 62+82=102
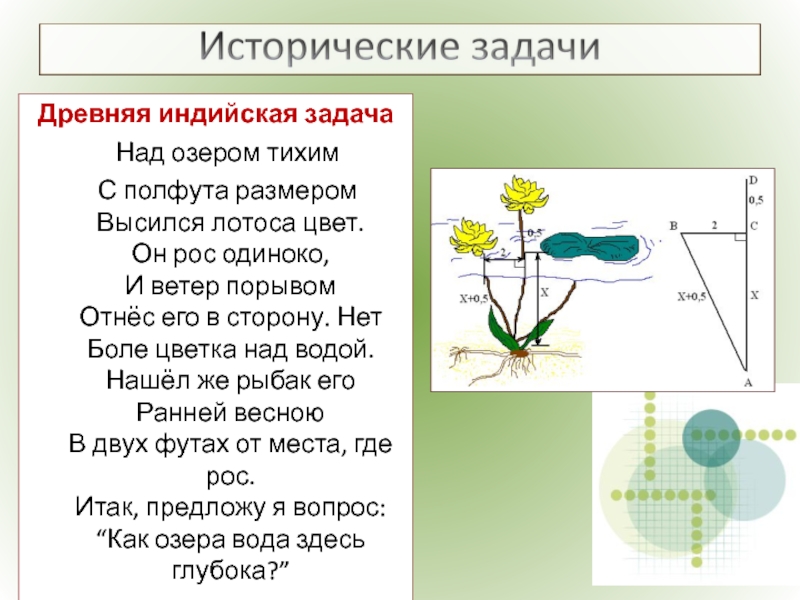
Слайд 13Древняя индийская задача
Над озером тихим
С полфута размером
Высился
Слайд 14Решение:
Пусть глубина реки = х, тогда при натяжении длина
5 х²+5²=(х+1)²
х²+5²=х²+2х+1
х+1 х х²+25=х²+2х+1
2х=24
х=12
тогда, глубина реки=12чи, следовательно, длина камыша = 13чи.
Слайд 16Задача индийского математика
XII века Бхаскары
"На берегу реки рос тополь одинокий.
Вдруг
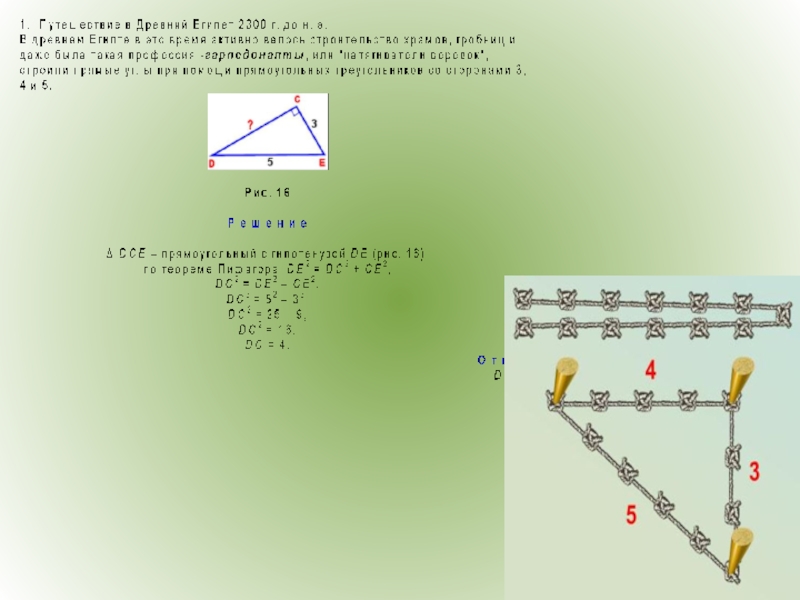
Слайд 17Задача из китайской
«Математики в девяти книгах»
"Имеется водоем со стороной в
Спрашивается: какова глубина воды и какова длина камыша?"
Слайд 18Задача из учебника "Арифметика"
Леонтия Магницкого
"Случися некому человеку к стене лестницу
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
1172=13689, 1252=15625
Слайд 19Задача из учебника "Арифметика"
Леонтия Магницкого
"Случися некому человеку к стене лестницу
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
Ответ: 44 шага
Слайд 20
Применение теоремы Пифагора
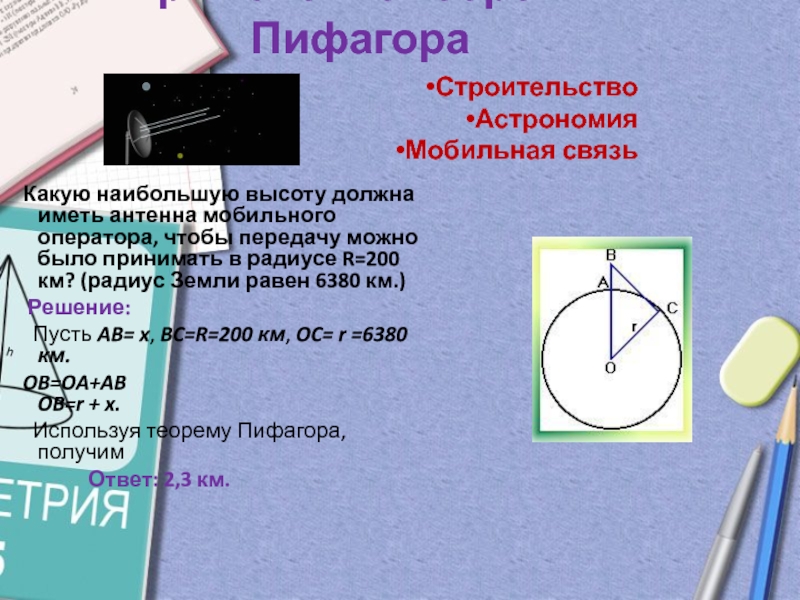
Какую наибольшую высоту должна иметь антенна
Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB OB=r + x.
Используя теорему Пифагора, получим
Ответ: 2,3 км.
Строительство
Астрономия
Мобильная связь
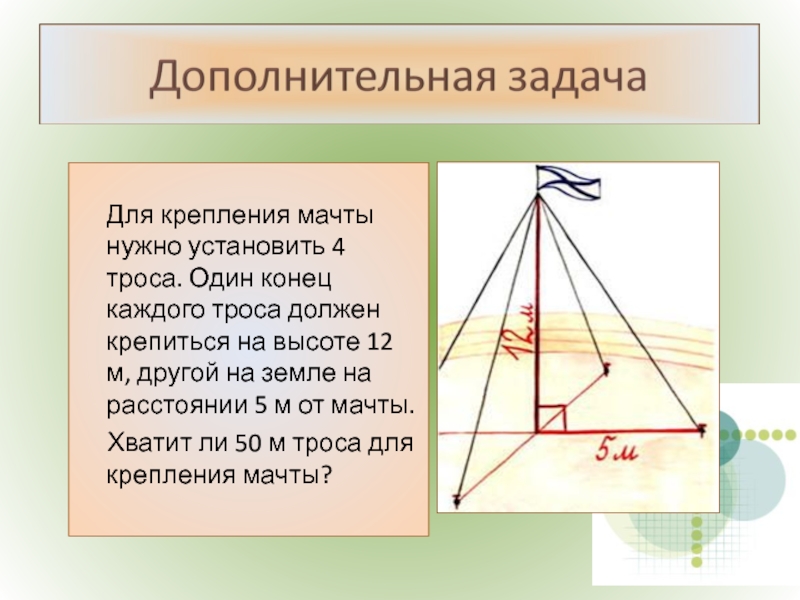
Слайд 21 Для крепления мачты нужно установить 4 троса. Один конец каждого троса
Хватит ли 50 м троса для крепления мачты?
Слайд 22Некоторые из 325 Пифагоровых заповедей:
Мысль – превыше всего между людьми.
Сыщи
Не гоняйся за счастьем: оно всегда находится в тебе самом.
Не пренебрегай здоровьем своего тела.
Либо молчи, либо говори то, что ценнее молчания.
Научись жить просто и без роскоши.
Не закрывай глаза, когда хочешь спать, не разобравши всех своих поступков за день.
Слайд 23Пифагорейцы с равным усердием заботились и о духовном развитии, и о
Слайд 24теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные;
создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Слайд 25
5см и 12 см, то гипотенуза равна… а) 15 см; б) 17 см; в) 13 см; г) 60 см. 9. Напишите, где применяется теорема Пифагора 10. Напишите, что интересного вы узнали на этом уроке.
Слайд 26Значение теоремы Пифагора
Как символ вечного союза
Как верной дружбы знак простой,
Связала ты
Навеки катеты с собой.
Путей окольных избегая
И древней истине верна,
Ты по характеру – прямая,
И по обычаю точна.
Скрывала тайну ты, но скоро
Явился некий мудрый грек.
И теоремой Пифагора,
Тебя прославил он на век.
Хранит тебя безмолвно, чинно
Углов сторожевой наряд;
И копья – острые вершины –
По обе стороны грозят.
И, если двоечник, конфузясь,
Немеет пред твоим лицом,
Пронзи его гипотенуза
Своим отточенным копьем!
Слайд 27О т е о р е м е П и ф а г о р а
Суть истины вся в том, что нам она – навечно,
Когда хоть
(Отрывок из стихотворения А. Шамиссо)