- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие множество и операции с ним презентация
Содержание
- 1. Понятие множество и операции с ним
- 2. План 1. Понятие «множество» и операции
- 3. Литература Белошистая А.В Формирование и развитие
- 5. 1. Множество и операции с ним Множество
- 6. Упражнения для определения множества Множество людей……
- 7. Свойства множества Множество характеризуется различными свойствами
- 8. Свойства множества Элементы множества -
- 9. Конечность и бесконечность множества Однородность и разнородность
- 10. Операции с множествами При объединение (сумме) двух
- 12. 2. Восприятие и отображение множества детьми раннего
- 13. Особенности восприятия Дети рано начинают
- 14. Особенности восприятия множества При восприятии
- 15. 3.Задачи и содержание обучения детей дискретным величинам
- 16. Содержание знаний о множестве включает: 1.
- 17. Термины, которыми овладевает ребенок: « много», «
- 18. Роль анализаторов в восприятии множеств зрительный (контролирующий);
- 19. Методы и приемы формирования представлений о множестве
- 20. Выводы: Множество-это……… Множество обладает рядом свойств……… Операции
Слайд 2План
1. Понятие «множество» и операции с ним
2.Восприятие и отображение множества
детьми раннего возраста
3. Задачи и содержание обучения детей дискретным величинам (множествам)
4. Методы и приемы формирования у детей представлений о множестве
3. Задачи и содержание обучения детей дискретным величинам (множествам)
4. Методы и приемы формирования у детей представлений о множестве
Слайд 3Литература
Белошистая А.В Формирование и развитие математических способностей дошкольников Курс лекций-
М.: Владос, 2004
Михайлова З.А. Теории и технологии математического развития детей дошкольного возраста.- СПБ, «ДЕТСТВО- ПРЕСС», 2008- 384с.
Шадрина И.В.Теория и методика математического развития : учебник и практикум для СПО.- М.: Юрайт, 2016, 279с.
Щербакова Е.И. Теория и методика математического развития дошкольников. – Воронеж, 2005- 392с
Михайлова З.А. Теории и технологии математического развития детей дошкольного возраста.- СПБ, «ДЕТСТВО- ПРЕСС», 2008- 384с.
Шадрина И.В.Теория и методика математического развития : учебник и практикум для СПО.- М.: Юрайт, 2016, 279с.
Щербакова Е.И. Теория и методика математического развития дошкольников. – Воронеж, 2005- 392с
Слайд 51. Множество и операции с ним
Множество - основное понятие в математике.
Множество - совокупность объектов, объединенных по какому-либо признаку и воспринимаемых как единое целое.
Понятие «множество» ввел Георг Кантор в 70 г ХІХв.
Понятие «множество» ввел Георг Кантор в 70 г ХІХв.
Слайд 6Упражнения для определения множества
Множество людей……
Множество птиц………
Множество пчел…….
Множество букв……
Множество военных……
Множество деревьев….
Слайд 7Свойства множества
Множество характеризуется различными свойствами (характеристиками). Под характеристиками подразумеваются такие
свойства, которыми владеют все объекты, принадлежащие данному множеству, и не владеет ни один предмет, который не принадлежит ему, т.е. не является его элементом.
Элементами множества называют объекты, составляющие его. Множества обозначается большими латинскими буквами А,В,С,D, а его элементы – малыми a,b,c,d
Элементами множества называют объекты, составляющие его. Множества обозначается большими латинскими буквами А,В,С,D, а его элементы – малыми a,b,c,d
Слайд 8Свойства множества
Элементы множества - объекты, из которых состоит множество (предметы,
звуки, движения, числа и т.д.).
Пустое множество - множество, не содержащее ни одного элемента (расстояние от стены до окна, поверхность доски).
Свойства множеств.
Мощность -это обобщение понятия количества (числа) элементов множества.
Равномощные множества – множества, равные по количеству элементов.
Неравномощные множества - множества, неравные по количеству элементов
Пустое множество - множество, не содержащее ни одного элемента (расстояние от стены до окна, поверхность доски).
Свойства множеств.
Мощность -это обобщение понятия количества (числа) элементов множества.
Равномощные множества – множества, равные по количеству элементов.
Неравномощные множества - множества, неравные по количеству элементов
Слайд 9Конечность и бесконечность множества
Однородность и разнородность
Конечное множество (если оно не пустое) -
множество, элементы которого можно "пересчитать"(есть начало и конец).
Бесконечное множество - множество, элементы которого нельзя "пересчитать"( нет конца).
Однородность и разнородность.
Однородные множества состоят из однотипных элементов;
Разнородные множества состоят из элементов, отличающихся одним или несколькими признаками.
Бесконечное множество - множество, элементы которого нельзя "пересчитать"( нет конца).
Однородность и разнородность.
Однородные множества состоят из однотипных элементов;
Разнородные множества состоят из элементов, отличающихся одним или несколькими признаками.
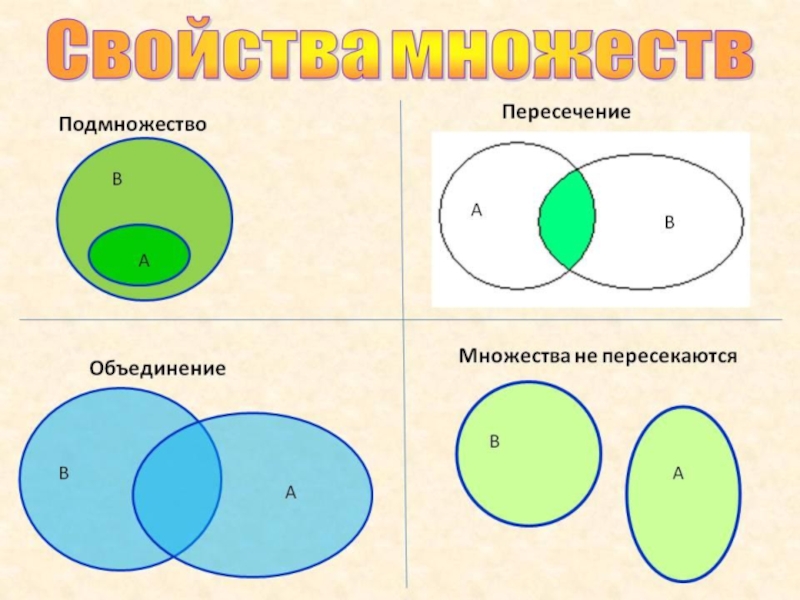
Слайд 10Операции с множествами
При объединение (сумме) двух множеств образуется третье множество, которое
включает все элементы этих множеств;
При вычитании множества образуется третье множество, которое называется разностью;
При пересечении двух множеств образуется третье множество, которое состоит из общих элементов
При вычитании множества образуется третье множество, которое называется разностью;
При пересечении двух множеств образуется третье множество, которое состоит из общих элементов
Слайд 122. Восприятие и отображение множества детьми раннего возраста
Первые экспериментальные исследования
по восприятию множества были проведены в начале 50-х гг. ( Г.С. Костюк, А.М Леушина, Н.А Менчинская). Учеными был выявлен ряд особенностей восприятия множества детьми раннего возраста
Слайд 13Особенности восприятия
Дети рано начинают выделять «один» и «много» ( на
втором году жизни)
Множество для ребенка раннего возраста не имеет четких границ (при выкладывании элементов множества фиксирует крайние элементы множества, не обращает внимания на промежуточные)
ребенок не выделяет элементы множества (не замечает, если из множества забрать 1-2- элемента, замечает лишь когда исчезает большая часть элементов множества);
При восприятии множества дети опираются на размер предметов (5 маленьких машин оцениваются ребенком как множество с меньшим количеством элементов по сравнению с 3 большими);
Множество для ребенка раннего возраста не имеет четких границ (при выкладывании элементов множества фиксирует крайние элементы множества, не обращает внимания на промежуточные)
ребенок не выделяет элементы множества (не замечает, если из множества забрать 1-2- элемента, замечает лишь когда исчезает большая часть элементов множества);
При восприятии множества дети опираются на размер предметов (5 маленьких машин оцениваются ребенком как множество с меньшим количеством элементов по сравнению с 3 большими);
Слайд 14Особенности восприятия
множества
При восприятии множества ориентируются на пространственный признак (при
сравнении двух одинаковых множеств, множество, элементы которого занимают большую площадь, оценивают как множество с большим количеством элементов (и наоборот);
Ориентируются на форму размещения элементов множества в пространстве (легче отображают множество, элементы которого размещены в ряд (хуже - по кругу, контуру квадрата и т.п.);
Сравнение множеств, установление равенства и неравенства осуществляется легче путем накладывания элементов друг на друга или же прикладыванием.
Ориентируются на форму размещения элементов множества в пространстве (легче отображают множество, элементы которого размещены в ряд (хуже - по кругу, контуру квадрата и т.п.);
Сравнение множеств, установление равенства и неравенства осуществляется легче путем накладывания элементов друг на друга или же прикладыванием.
Слайд 153.Задачи и содержание обучения детей дискретным величинам
1. Формировать представления о
границах множества и его элементов;
2. способствовать представлениям о равенстве и неравенстве групп по количеству элементов;
3. Развивать умения и навыки в поэлементном сравнении контрастных и смежных множеств;
4. Упражнять в навыках накладывания и прикладывания, установления взаимно однозначного соответствия;
5. Обогащать речь ребенка специальной терминологией
2. способствовать представлениям о равенстве и неравенстве групп по количеству элементов;
3. Развивать умения и навыки в поэлементном сравнении контрастных и смежных множеств;
4. Упражнять в навыках накладывания и прикладывания, установления взаимно однозначного соответствия;
5. Обогащать речь ребенка специальной терминологией
Слайд 16Содержание знаний о множестве включает:
1. Понимание, что несколько предметов, находящихся рядом,
обозначаются словом «много», одиночные предметы –словом «один»;
2. Понимание вопроса»сколько?», выражений «столько-сколько», «поровну», «больше-меньше»;
3. Умение составлять группу из отдельных предметов
(1, еще 1,еще 1- много);
4. Разделять группу на отдельные предметы;
5. Знать равенства и неравенства групп по количеству элементов (кубиков и кирпичиков поровну, кубиков больше, чем кирпичиков и наоборот);
2. Понимание вопроса»сколько?», выражений «столько-сколько», «поровну», «больше-меньше»;
3. Умение составлять группу из отдельных предметов
(1, еще 1,еще 1- много);
4. Разделять группу на отдельные предметы;
5. Знать равенства и неравенства групп по количеству элементов (кубиков и кирпичиков поровну, кубиков больше, чем кирпичиков и наоборот);
Слайд 17Термины, которыми овладевает ребенок:
« много», « мало», «один», «по одному», «
ни одного»;
«больше на один», «меньше на один»;
«столько- сколько», «поровну»;
« сравнение», « накладывание», «прикладывание»;
«сравнить»,«увеличить»,
«уменьшить», «наложить», «приложить»
«больше на один», «меньше на один»;
«столько- сколько», «поровну»;
« сравнение», « накладывание», «прикладывание»;
«сравнить»,«увеличить»,
«уменьшить», «наложить», «приложить»
Слайд 18Роль анализаторов в восприятии множеств
зрительный (контролирующий);
двигательный (дробный, так как он позволяет
разбивать множество на отдельные элементы);
слуховой;
осязательный- на ощупь (рамки- вкладыши, карточки с нашитыми пуговицами);
кинестетический.
Чем больше включено анализаторов, тем процесс восприятия множества эффективнее
слуховой;
осязательный- на ощупь (рамки- вкладыши, карточки с нашитыми пуговицами);
кинестетический.
Чем больше включено анализаторов, тем процесс восприятия множества эффективнее
Слайд 19Методы и приемы формирования представлений о множестве
Основными методами формирования представлений о
множестве являются дидактические игры и упражнения с конкретными множествами;
а также метод сравнения, сопоставления множеств друг с другом (для выявления одного и множества, равенства и неравенства и т.п.);
основными приемами являются приемы наложения и приложения (накладывания и прикладывания)
а также метод сравнения, сопоставления множеств друг с другом (для выявления одного и множества, равенства и неравенства и т.п.);
основными приемами являются приемы наложения и приложения (накладывания и прикладывания)
Слайд 20Выводы:
Множество-это………
Множество обладает рядом свойств………
Операции с множествами - это……….
Особенности детского восприятия множества
в………..
Задачи по ознакомлению с множествами…….
Методы и приемы формирования понятий о множестве……………..
Задачи по ознакомлению с множествами…….
Методы и приемы формирования понятий о множестве……………..