- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Отношения между понятиями презентация
Содержание
- 1. Отношения между понятиями
- 2. Есть ли общие признаки в содержании понятий?
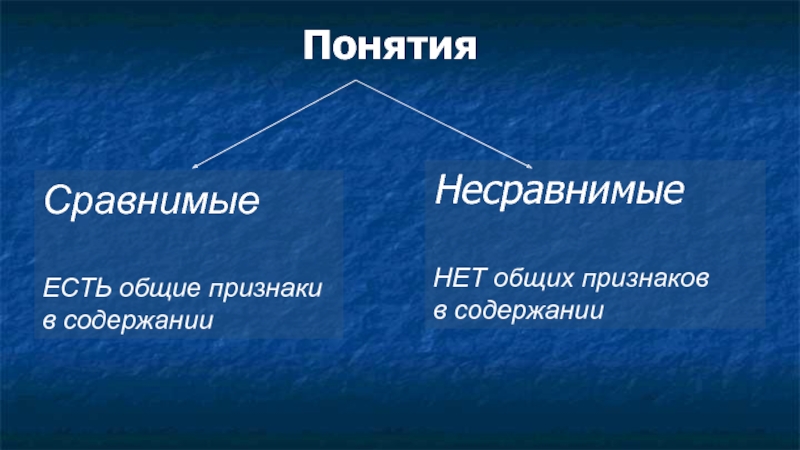
- 3. Понятия Сравнимые ЕСТЬ общие признаки в содержании Несравнимые НЕТ общих признаков в содержании
- 4. Несравнимые понятия Только философские категории Материальное – идеальное Конкретное – абстрактное Объективное - субъективное
- 5. Сравнимые понятия (есть общие признаки в содержании) Есть ли общие элементы в объеме?
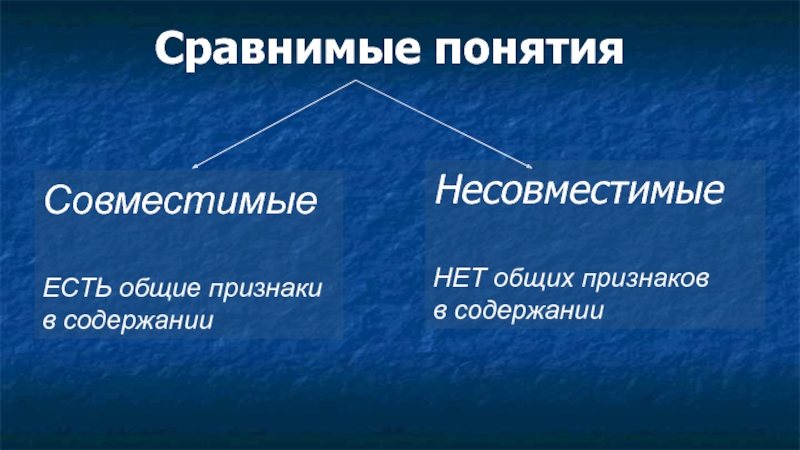
- 6. Сравнимые понятия Совместимые ЕСТЬ общие признаки
- 7. Примеры А – студент В
- 8. Совестимые понятия Тождественные (равнообъемные) Перекрещивающиеся
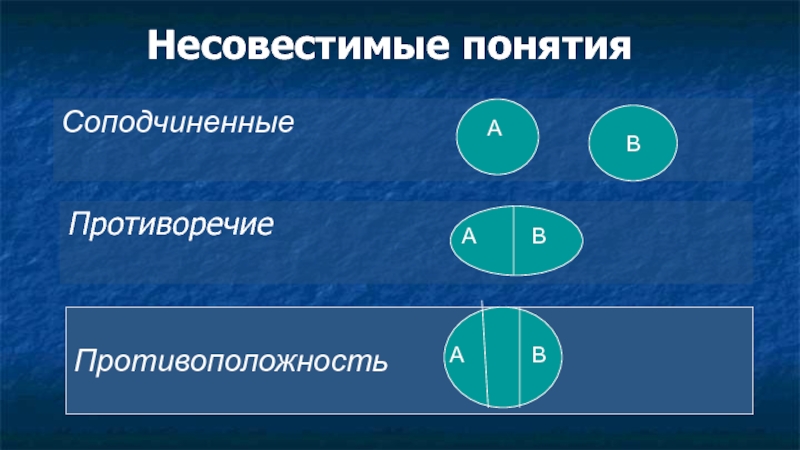
- 9. Несовестимые понятия Соподчиненные Противоречие
- 10. Пример (задание № 2) Определить вид отношений
- 11. Определяем, есть ли единичные понятия Объемы единичных понятий изображаются точками.
- 12. Отношения определяются отдельно в каждой паре
- 13. Это мы нарисовали объем понятия 1 – населенный пункт (понятие общее) 1
- 14. Является ли какой-то населенный пункт городом? ДА
- 15. Теперь будем выяснять, какой в данном случае вид совместимости ЛЮБОЙ ли населенный пункт – город?
- 16. НЕТ – значит это не тождественные
- 17. Чем отличаются? Перекрещивающиеся Родо-видовые (подчиненные) А В в А
- 18. У подчиненного понятия В объем полностью входит
- 19. ЛЮБОЙ ли город является населенным пунктом? ДА - значит понятия 1 и 2 - ПОДЧИНЕННЫЕ
- 20. 2 1
- 21. Работаем с понятиями 1 и 3:
- 22. 1 * 3
- 23. Работаем с понятиями 1 и 4:
- 24. Выясняем, какой у нас вид несовместимости. Начинаем с самого простого варианта несовместимости – Противоречия
- 25. Если понятия 1 и 4 противоречащие, то 1 4
- 26. Это означает, что как только предмет не
- 27. НЕТ - значит это не противоречащие понятия Теперь выясним, являются они противоположными или соподчиненными
- 28. Выясним: В мире - населенный пункт, городской
- 29. Понятия 1 и 4 – соподчиненные 1 4
- 30. Аналогично определяем отношения в парах: 2-3; 2-4
- 31. Аналогично определяем отношения в паре: 3-4 4 соподчинение * 3
- 32. ОБЩАЯ схема отношений между понятиями
- 33. § 4. Операции над понятиями Когда мы
- 34. Операции над объемом понятия Объем Уменьшить
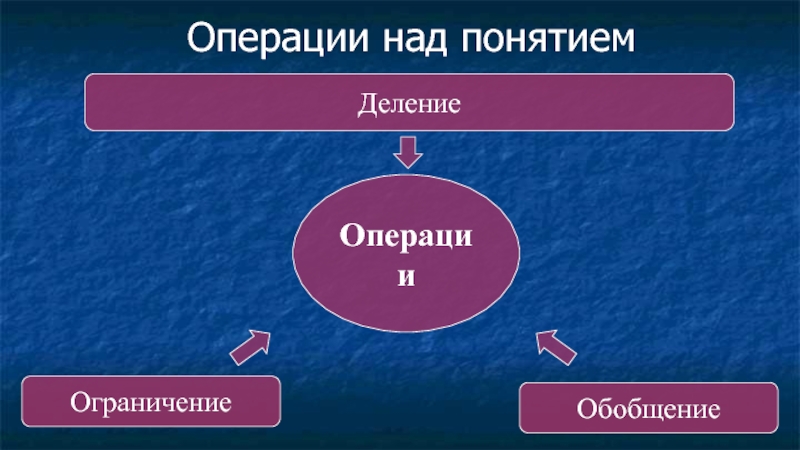
- 35. Операции над понятием Операции Ограничение Обобщение Деление
- 36. П.1. Ограничение понятия. Логическая операция над
- 37. Круговые схемы А - студент
- 38. Есть ли предел ограничения понятия?
- 39. П.2. Обобщение понятия. Логическая операция над
- 40. Круговые схемы А –министерство финансов
- 41. Есть ли предел обобщения понятия?
- 42. Пример. Обобщить понятие до предела, совершив 3
- 43. П.3. Деление понятия. Логическая операция над
- 44. Виды деления: Деление на 2 класса
- 45. Дихотомическое деление: Деление всегда правильное Деление
- 46. Деление по видоизменению признака: За один
- 47. ЗАМЕЧАНИЕ: Закон обратного отношения справедлив
- 48. Правила деления: 2. Члены
- 49. Правила деления: - Не
- 50. Пример (задание № 3): Проверить правильность деления
Слайд 2Есть ли общие признаки в содержании понятий?
А- Студент
А- Студент В – подводная лодка;
А – Студент В – государство;
Слайд 4Несравнимые понятия
Только философские категории
Материальное – идеальное
Конкретное – абстрактное
Объективное - субъективное
Слайд 6Сравнимые понятия
Совместимые
ЕСТЬ общие признаки
в содержании
Несовместимые
НЕТ общих признаков
в содержании
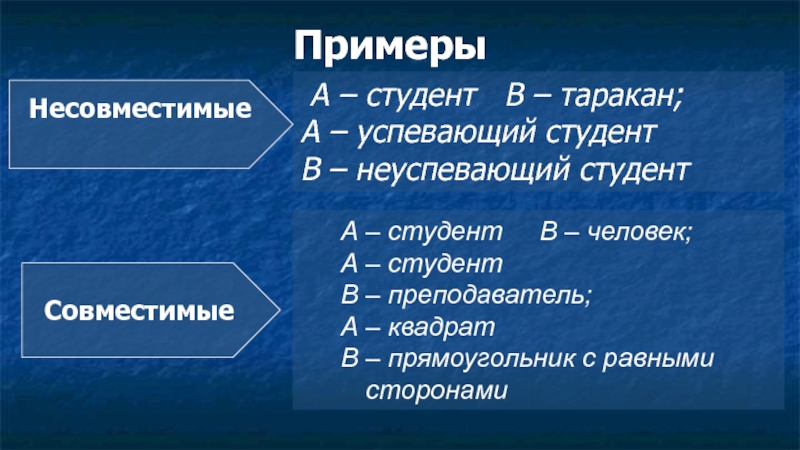
Слайд 7Примеры
А – студент В – таракан;
А – успевающий студент
В
Несовместимые
Совместимые
А – студент В – человек;
А – студент
В – преподаватель;
А – квадрат
В – прямоугольник с равными сторонами
Слайд 8Совестимые понятия
Тождественные (равнообъемные)
Перекрещивающиеся
Родо-видовые (подчиненные)
А=В
А
В
в
А
Слайд 10Пример (задание № 2)
Определить вид отношений между понятиями, изобразив их объемы
Населенный пункт – город – город Оренбург – городской житель
Слайд 12Отношения определяются отдельно
в каждой паре понятий
Сначала определяем отношения в парах:
Слайд 14Является ли какой-то населенный пункт городом?
ДА – значит понятия 1 и
(НЕТ - понятия несовместимые)
Слайд 15Теперь будем выяснять, какой в данном случае вид совместимости
ЛЮБОЙ ли населенный
Слайд 16НЕТ
– значит это не тождественные понятия
Теперь будем выяснять, являются они
Слайд 18У подчиненного понятия В объем полностью входит
в объем А
У перекрещивающегося
Слайд 21Работаем с понятиями 1 и 3:
Является ли город Оренбург населенным пунктом?
ДА
-
Слайд 23Работаем с понятиями 1 и 4:
Является ли какой-то городской житель населенным
НЕТ
- значит понятия 1 и 4 - НЕСОВМЕСТИМЫЕ
Слайд 24Выясняем, какой у нас вид несовместимости.
Начинаем с самого простого варианта несовместимости
Противоречия
Слайд 26Это означает, что как только предмет не 1 (населенный пункт), то
Так ли это?
Слайд 27НЕТ
- значит это не противоречащие понятия
Теперь выясним, являются они противоположными или
Слайд 28Выясним:
В мире - населенный пункт, городской житель и что-то «среднее» между
В мире – населенный пункт, городской житель и МНОГОЕ ДРУГОЕ?
Слайд 33§ 4. Операции над понятиями
Когда мы оперируем с понятием мы
что-то
Что можно сделать с объемом?
Слайд 34Операции над объемом понятия
Объем
Уменьшить
Увеличить
Оставить без изменения, но разбить на классы
Слайд 36П.1. Ограничение понятия.
Логическая операция над понятием, в результате которой объем
Ограничение
Пример
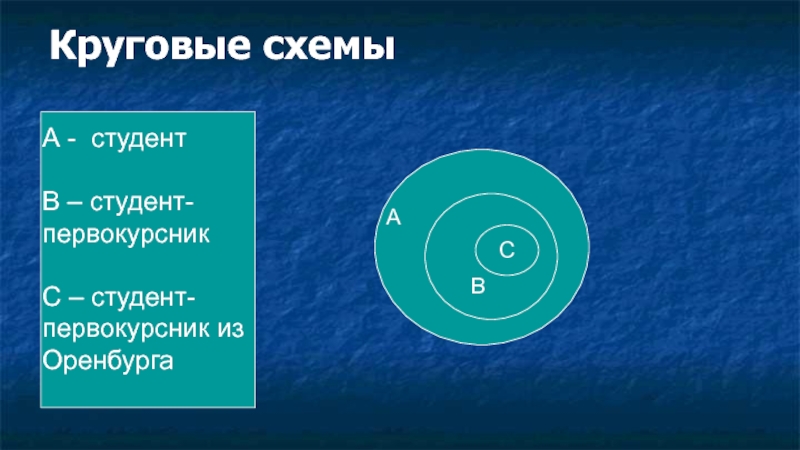
А – студент;
В – студент-первокурсник;
С – студент-первокурсник из Оренбурга
Слайд 39П.2. Обобщение понятия.
Логическая операция над понятием, в результате которой объем
Обобщение
Пример
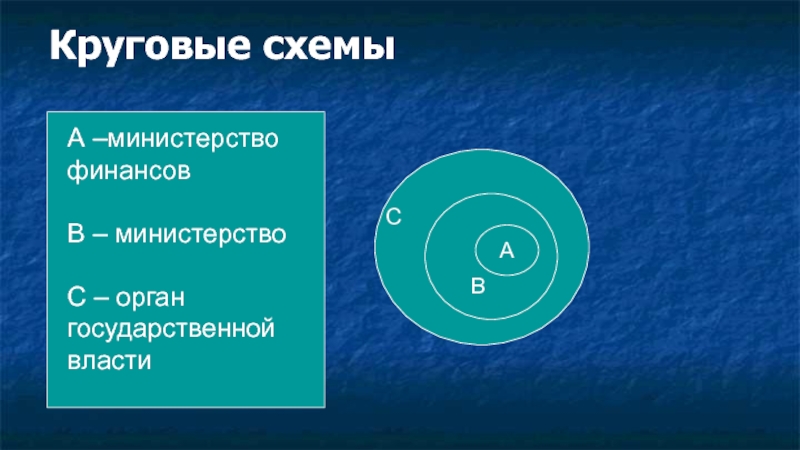
А – Министерство финансов;
В – Министерство;
С – Орган государственной власти
Слайд 42Пример. Обобщить понятие до предела, совершив 3 шага обощения.
А -
В – Учащийся
С – Человек
Д - Материальное
Д
А
В
С
Слайд 43П.3. Деление понятия.
Логическая операция над понятием, в результате которой объем
Деление
Пример
А – студент
В – веселый студент
С – грустный студент
Д – «средний» студент
Слайд 44Виды деления:
Деление на 2 класса
Эти классы – противоречащие понятия
Дихотомическое
По видоизменению
признака
Деление
Деление на 2 класса, но они не являются противоречащими понятиями
Слайд 45Дихотомическое деление:
Деление всегда правильное
Деление простое
Достоинства
Недостатки
За один шаг деления могут получиться
Слайд 46Деление по видоизменению признака:
За один шаг получаем нужные по объему
Достоинства
Недостатки
Деление сложное
Часто оно неправильное. Чтобы гарантировать правильность, надо проверять ПРАВИЛА ДЕЛЕНИЯ
Слайд 47ЗАМЕЧАНИЕ:
Закон обратного отношения справедлив
только для логических объемов понятий.
Закон обратного
(добавление признака к содержанию понятия может не привести к уменьшению его объема, так как этот признак мог неявно уже присутствовать в содержании понятия)
Слайд 48Правила деления:
2. Члены деления должны исключать друг друга
1. Деление должно
3. Деление должно быть непрерывным, без скачков
(Скачок – если члены деления нарушают свой уровень.
Есть всегда, когда члены деления, выделенные по разным основаниям, стоят на одном уровне
Слайд 49Правила деления:
- Не широким (не содержать пустых понятий среди членов
4. Деление должно быть соразмерным:
- Не узким, то есть содержать все виды делимого понятия, выделенные по данному основанию
Слайд 50Пример (задание № 3):
Проверить правильность деления понятия. В случае обнаружения ошибок,
Среди студентов есть те, кто пропускает
лекции всегда, и те, кто пропускает лекции
иногда.