- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Факторы динамики численности популяций презентация
Содержание
- 1. Факторы динамики численности популяций
- 2. Численность популяции никогда не остается постоянной, она
- 3. = (В + im) – (D +
- 4. Если величинами im и em можно пренебречь,
- 5. Рождаемость в популяциях определяется, преимущественно свойствами особей
- 6. Тем не менее, на все эти
- 7. Абсолютная плодовитость (F) У одноклеточных организмов,
- 8. Ниже своего максимального уровня, плодовитость, особенно у
- 9. Это связь обычно выражается степенным уравнением:
- 10. Зависимость плодовитости (F, яйца·особь-1)
- 11. Часто достижения самками
- 12. Характер изменения плодовитости пойкилотермных животных с концентрацией
- 13. Концентрация корма Детритофаги и хищники
- 14. Влияние плотности популяции на плодовитость животных (схема)
- 15. Однако во всех случаях выявлена одна общая
- 16. Длительность генеративного цикла (G) У одноклеточных организмов
- 17. У гомойотермных животных длительность эмбриогенеза (беременность у
- 18. Длительность беременности у млекопитающих в целом возрастает
- 19. Период насиживания у птиц в целом возрастает
- 20. Время генерации (Тo), или продолжительность жизни одного
- 21. Доля размножающихся самок в общей численности популяции
- 22. Скорость размножения особи равна среднему количеству потомков
- 23. Скорость размножения популяции равна
- 24. Bp =
- 25. Пример для дафнии Daphnia magna F
- 26. Удельная рождаемость
- 27. В таком случае увеличение
- 28. Значение b
- 29. Рассчитаем значение b для популяции инфузории за
- 30. Однако большинство видов размножается путем продуцирования молоди
- 31. Допустим, популяция состоит
- 32. Пример для партеногенетической популяции Daphnia magna.
- 33. Если в популяции
- 34. Пример для двуполой популяции Asellus aquaticus
- 35. Типы смертности в популяциях
- 36. 1а
- 37. I-й тип смертности Отражает
- 38. Ia-тип смертности Ступенчатая кривая характерна для
- 39. II-ой тип смертности
- 40. III-й тип смертности
- 42. Кривые выживания в когортах
- 43. Удельную скорость смертности (d) в когорте (при
- 44. Если за достаточно длительный период
- 45. Отсюда возможно определить
- 46. Сопряженные изменения рождаемости и смертности
- 47. N bo do Высокая смертность
- 48. Тогда bN =
- 49. Когда bo = do, что соответствует точке
- 50. При стационарном состоянии популяции,
- 51. do Во многих случаях
- 52. В таком случае существует не только максимальный
- 53. Рост численности популяций
- 54. Значение
- 55. Относительная скорость роста
- 56. Удельную скорость
- 57. В таком случае
- 58. В
- 59. Примеры экспоненциального роста популяции от No =
- 60. Уравнение экспоненциально роста
- 61. В природных
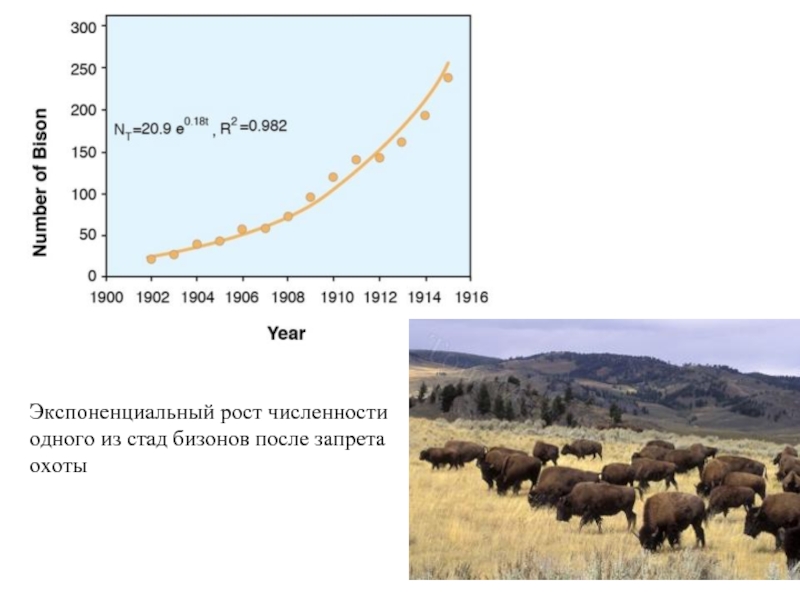
- 62. Экспоненциальный рост численности одного из стад бизонов после запрета охоты
- 63. Логистический рост численности
- 64. Рассмотрим простейший случай, когда удельная скорость
- 65. Тогда связь между r
- 66. Подставляя a = r/K
- 68. Преобразуем уравнение: Получаем: Значение
- 69. При
- 70. Интегрирование уравнения
- 71. График логистического уравнения
- 73. t = 0 cуток, N
- 74. Рост численности популяции дрозофилы
- 75. Емкость среды
- 76. Емкость среды проявляет
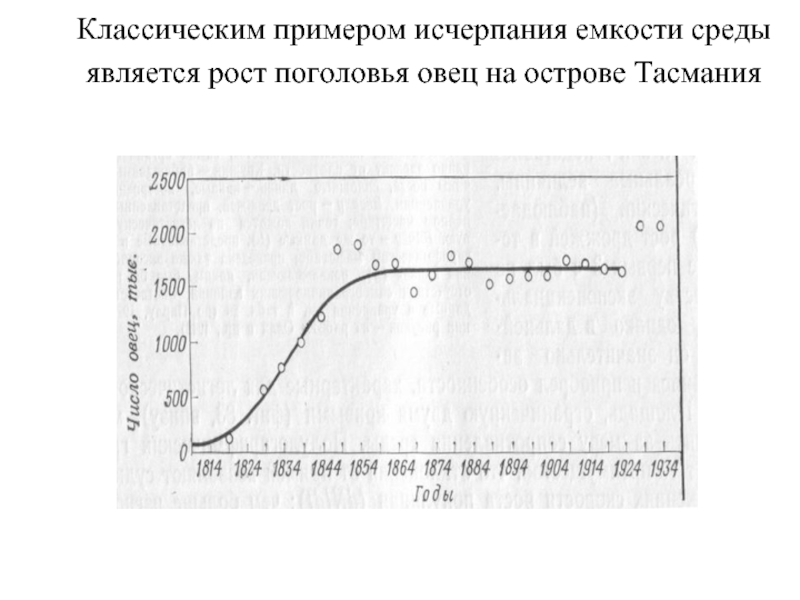
- 77. Классическим примером исчерпания емкости среды является рост поголовья овец на острове Тасмания
Слайд 2 Численность популяции никогда не остается постоянной, она постоянно претерпевает сезонные или
В общем виде изменения численности популяции за единицу времени определяются следующим образом:
Слайд 3= (В + im) – (D + em),
где:
В - рождаемость, или
D – смертность, или количество погибших особей в популяции, независимо от причины их смерти – старость, выедание хищниками, болезни, промысел, гибель в природных катастрофах и т.д.;
im – иммиграция, или число особей, поступивших в данную популяцию из других популяций;
em – эмиграция, или число особей, убывших из данной популяции в другие популяции.
Все эти параметры определяются для определенных промежутков времени (сутки, месяц, год и т.д.) и имеют размерность [особь·время-1].
Слайд 4 Если величинами im и em можно пренебречь, то изменения численности популяции
= В – D,
При В = D численность популяции остается постоянной, поскольку
При В > D она возрастает,
а при В < D – снижается.
.
Слайд 5 Рождаемость в популяциях определяется, преимущественно свойствами особей и популяций, из которых
Абсолютная, или индивидуальная плодовитость – число потомков (яйца, личинки, молодь, семена, споры и т.п.), производимых материнской особью за один акт размножения;
Длительность генеративного цикла, или промежутка времени между двумя последовательными актами размножения у отдельных особей;
Время генерации, или продолжительность жизни одного поколения.
Общая численность (плотность) популяции;
Доля особей, производящих потомство, в популяции.
Слайд 6
Тем не менее, на все эти параметры рождаемости существенное воздействие оказывают
Смертность в популяциях, напротив, определяют, прежде всего, внешние факторы, которые кратко были перечислены выше.
Поэтому, хотя каждый вид имеет генетически закрепленную максимальную длительность жизни, в природных условиях до нее доживает лишь незначительная часть популяции.
Слайд 7 Абсолютная плодовитость (F)
У одноклеточных организмов, размножающихся делением надвое (бактерии, протисты),
Плодовитость гомойотермных животных очень низка – от 1 до 5 – 7, очень редко до 12 – 15 детенышей (серая полевка, крыса) и 20 – 22 яиц (куриные птицы).
У пойкилотермных организмов Е, как правило, значительно выше – от нескольких десятков и сотен – у травянистых растений, коловраток, ракообразных, брюхоногих моллюсков, амфибий, рептилий – до сотен тысяч и миллионов – у древесных растений, грибов, крупных двустворчатых моллюсков и рыб.
Если число потомков, произведенных за один акт размножения, больше единицы, их совокупность, особенно у животных, часто называют кладкой или пометом.
Слайд 8 Ниже своего максимального уровня, плодовитость, особенно у видов с достаточно высокими
У птиц и млекопитающих F практически не зависит от размеров самок.
У большинства пойкилотермных животных, а также многих древесных растений в условиях, близких к оптимальным, значения F возрастают с увеличением размеров материнских особей (L).
Слайд 9 Это связь обычно выражается степенным уравнением:
F = mLn
где m и n - константы.
В логарифмических координатах данное уравнение трансформируется в уравнение прямолинейной регрессии
lgF = lgm + nlgL
У моллюсков, ракообразных и насекомых значения показателя степени n чаще всего изменяются в пределах от 2 до 3, у рыб обычно n > 3.
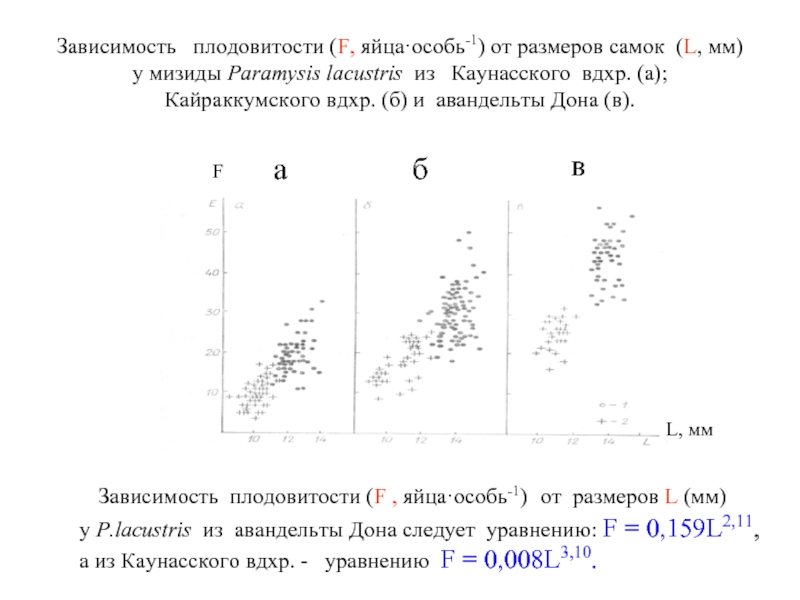
Слайд 10 Зависимость плодовитости (F, яйца·особь-1) от размеров самок (L, мм) у
Зависимость плодовитости (F , яйца·особь-1) от размеров L (мм)
у P.lacustris из авандельты Дона следует уравнению: F = 0,159L2,11,
а из Каунасского вдхр. - уравнению F = 0,008L3,10.
а
б
в
L, мм
F
Слайд 11 Часто достижения самками определенного возраста (обычно близкого
Возрастные изменения
плодовитости (F) у не-которых ракообразных
Возраст
F
Слайд 12 Характер изменения плодовитости пойкилотермных животных с концентрацией корма в среде (C)
Животных в этом отношении можно разделить на:
хищников, включая и растительноядных животных,
детритофагов, или «мусорщиков» (потребителей крупных органических остатков);
фильтраторов.
Слайд 13
Концентрация корма
Детритофаги и хищники
Фильтраторы
Зависимость между плодовитостью (F) и концентрацией корма у
F
Слайд 14Влияние плотности популяции на плодовитость животных (схема)
а
б
в
а – кривая «дрозофильного
б – кривая «типа Олли»
в – кривая промежуточного типа
П л о т н о с т ь п о п у л я ц и и
N
Слайд 15 Однако во всех случаях выявлена одна общая закономерность – при достижении
Это является одним из важнейших механизмов регуляции численности популяций по принципу отрицательной обратной связи.
Слайд 16Длительность генеративного цикла (G)
У одноклеточных организмов (бактерии, протисты) G соответствует промежутку
У многоклеточных организмов, особенно у мелких зоопланктонных видов (ракообразные, коловратки), дающих за сезон размножения несколько кладок, G часто принимается равным длительности эмбрионального развития яиц.
Слайд 17 У гомойотермных животных длительность эмбриогенеза (беременность у млекопитающих, насиживание яиц у
Она не зависит от температуры, но может изменяться в некоторых пределах под воздействием других факторов – условий питания, плотности популяции и т.д.
Слайд 18 Длительность беременности у млекопитающих в целом возрастает с увеличением их размеров:
Однако из этого правила имеются многочисленные исключения. Например, у барсука (масса тела до 16 кг) беременность длится дольше (357 суток), чем у гораздо более крупной лошади (400 кг и 330 суток).
У сумчатых, хищных и других млекопитающих, рождающих слепых и беспомощных детенышей, беременность обычно короче, чем у копытных с сопоставимой массой тела, детеныши которых способны следовать за матерью уже через несколько минут после рождения.
Слайд 19 Период насиживания у птиц в целом возрастает с увеличением массы яиц
Однако самые крупные среди современных птиц яйца африканского страуса (до 2 кг) насиживаются всего 35 - 42 суток, примерно столько же, как и небольшие яйца лебедя (35 г).
Слайд 20 Время генерации (Тo), или продолжительность жизни одного поколения.
У моноциклических видов (лососевые рыбы и др.), погибающих сразу же после вымета своей первой и единственной кладки, Tо совпадает со средней длительностью жизни половозрелых особей.
У полициклических видов, производящих две и более кладок за жизненный цикл, Tо определяется по специальным демографическим таблицам.
Слайд 21 Доля размножающихся самок в общей численности популяции (α ) равна
α
где
N♀ - численность размножающихся самок,
N – общая численность популяции.
Слайд 22 Скорость размножения особи равна среднему количеству потомков (яйца, личинки, молодь и
Br =
где
F – плодовитость особи;
G - длительности генеративного цикла, который в ряде случаев можно принять равным длительности эмбриогенеза (De)
Слайд 23 Скорость размножения популяции равна общему количеству потомков, произведенному
Bp =
где -
F – средняя плодовитость самок
G – длительность генеративного цикла
N - численность популяции
α – доля размножающихся самок в ней.
Слайд 25Пример для дафнии Daphnia magna
F = 30 яиц
G при 20оС
N = 500 экз м-3
α = 0,1
Отсюда,
Br = 30/3 = 10 яиц• сут-1,
Bp = (30• 500• 0,1)/3 = 500 яиц • м-3•сут-1
Слайд 26 Удельная рождаемость
Например, если инфузория Paramecium caudautum делится надвое всего раз в сутки, то численность ее популяции будет удваиваться каждые сутки.
При отсутствии смертности число потомков одной инфузории уже через год достигла бы 2364 (или 10110) особей.
Слайд 27 В таком случае увеличение численности популяции в геометрической
Nt = Noebt
где N0 – начальная численность особей
при t = 0,
Nt - численность особей ко времени t,
b - константа, называемая удельной рождаемостью.
Значение b означает количество потомков, которое производится в популяции за единицу времени в расчете на одну особь. Оно имеет размерность [время-1].
Слайд 28 Значение b может быть рассчитано, если
Слайд 29 Рассчитаем значение b для популяции инфузории за период времени t2 –
Поскольку численность популяции каждые сутки удваивается, то N2 = 2N1.
Отсюда:
b = (ln2N1 - lnN1)/1 =
= ln2 + lnN1 - lnN1 = ln2.
Отсюда b = 0,69 сут-1,
Уравнение роста для популяции инфузории в численной форме имеет вид:
Nt = N0e0,69t
Слайд 30 Однако большинство видов размножается путем продуцирования молоди или яиц, число которых
Значения b для популяций таких видов рассчитываются иными способами.
Рассмотрим вначале виды с партеногенетическим размножением, у которых потомство производят все половозрелые особи.
Их примером являются ветвистоусые ракообразные – дафнии и др.
Слайд 31 Допустим, популяция состоит только из половозрелых особей.
Если ее начальная численность (N1) равна 1 экз, то через 1 сутки она достигнет:
N2 = 1 + F/D.
Отсюда:
b = [ln(1 + F/D) - ln1]/1
Поскольку F/D представляет собой скорость размножения особей ( Br) и ln1 = 0, получаем:
b = ln(1 + Br)
Слайд 32Пример для партеногенетической популяции Daphnia magna.
Отсюда:
b = ln(1 + 30/3) = 2,40 сут-1
Слайд 33 Если в популяции имеются особи, не производящие
Тогда:
b = ln(1 + αBr)
Слайд 34Пример для двуполой популяции
Asellus aquaticus
F = 30 яиц
α = 0,1.
Тогда
b = ln (1 + 0,1 . 30/14) = 0,194 сут-1
.
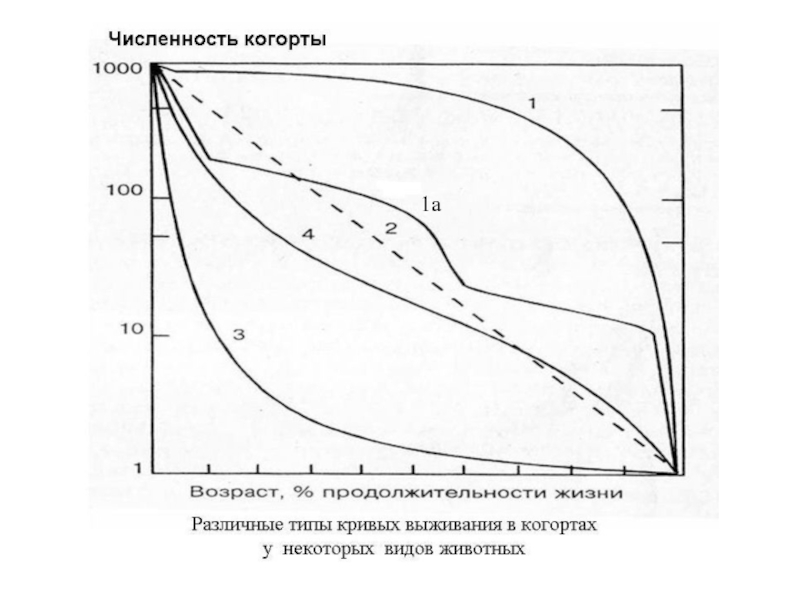
Слайд 35Типы смертности в популяциях
Мы будет анализировать смертность
Все особи в популяциях I-го типа составляют одну когорту.
Выделяют четыре основных типа смертности в когортах:
Слайд 37I-й тип смертности
Отражает ситуацию, при которой смертность до
Характерен для многих насекомых с неполным превращением, пресмыкающихся, большинства млекопитающих, в том числе человека.
Слайд 38Ia-тип смертности
Ступенчатая кривая характерна для видов с метаморфозом, у которых
Их примером являются насекомые с полным превращением – бабочки и др. Смертность их яиц и имаго выше, чем личинок и куколок.
Слайд 39II-ой тип смертности
Характеризует относительное постоянство смертности во
Свойственен преимущественно выводковым птицам, мелким млекопитающим (мыши, кролики) и некоторым другим видам, напр., рептилиям.
Слайд 40III-й тип смертности
Характеризуется очень высокой
Эти виды производят огромное количество семян, мелких икринок, личинок и т.п. До половой зрелости доживает лишь их ничтожная часть, однако смертность взрослых особей, после достижения ими определенных размеров достаточно низка.
Поэтому III тип смертности иногда называют устричным типом смертности.
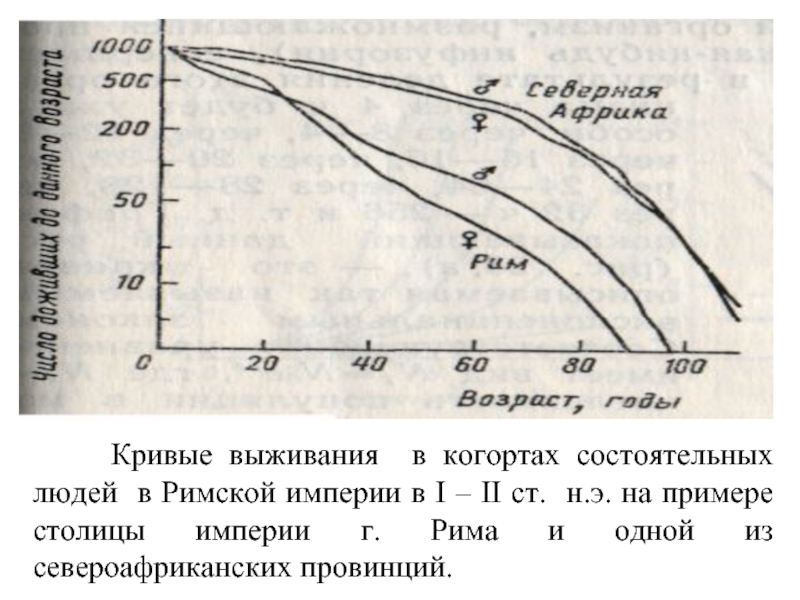
Слайд 42 Кривые выживания в когортах состоятельных людей в Римской
Слайд 43 Удельную скорость смертности (d) в когорте (при любых ее типах) за
Поскольку N2 < N1, значения d являются отрицательным и имеют размерность [время-1].
Они показывают число погибших особей в популяции за единицу времени в расчете на одну особь.
Слайд 44 Если за достаточно длительный период времени значения d остаются
В случае постоянства d за весь жизненный цикл получаем экспоненциальное снижение численности когорты:
Nt = Noe-dt,
где No - начальная численность особей в когорте, Nt – ее численность к возрасту t, d – удельная скорость смертности.
Легко видеть, что постоянство d в когорте соответствует II-му типу смертности.
Слайд 45 Отсюда возможно определить среднее значение максимальной длительности
Таковой можно принять возраст, до которого доживает 1% от начальной численности когорты. Если No = 100 особей, то Nt = 1 особь. Тогда
1 = 100e– dt
Отсюда
tmax = ln100/d = 4,6/d.
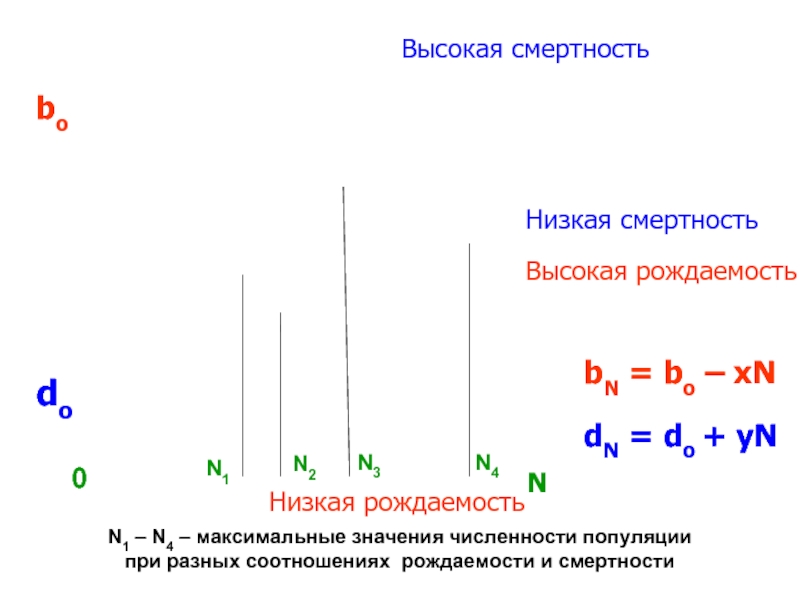
Слайд 46Сопряженные изменения рождаемости
и смертности
Рассмотрим простейший случай, когда удельная скорость смертности
Слайд 47
N
bo
do
Высокая смертность
Низкая смертность
Высокая рождаемость
Низкая рождаемость
bN = bo – xN
dN =
N1
N2
N3
N4
N1 – N4 – максимальные значения численности популяции
при разных соотношениях рождаемости и смертности
0
Слайд 48 Тогда
bN = bo – xN;
dN = do + yN
bN и dN –удельные скорости рождаемости и смертности при плотности N,
bo и do их значения при N, близкой к нулю,
х и у – эмпирические коэффициенты.
Слайд 49 Когда bo = do, что соответствует точке пересечения прямых) на графике,
Отсюда популяция достигает максимально возможной при данных условиях численности (Nmax), или т.наз. «стационарного состояния».
Чем сильнее рождаемость снижается, а смертность возрастает с увеличением плотности, тем более низкими становятся значения Nmax
Слайд 50 При стационарном состоянии популяции, т.е. при bN=dN
bo – xN = do + yN
Отсюда
Nmax = (bo – do)/(x + y)
Тогда плотность популяции может изменяться в следующих пределах:
0 ≤ N ≤ Nmax
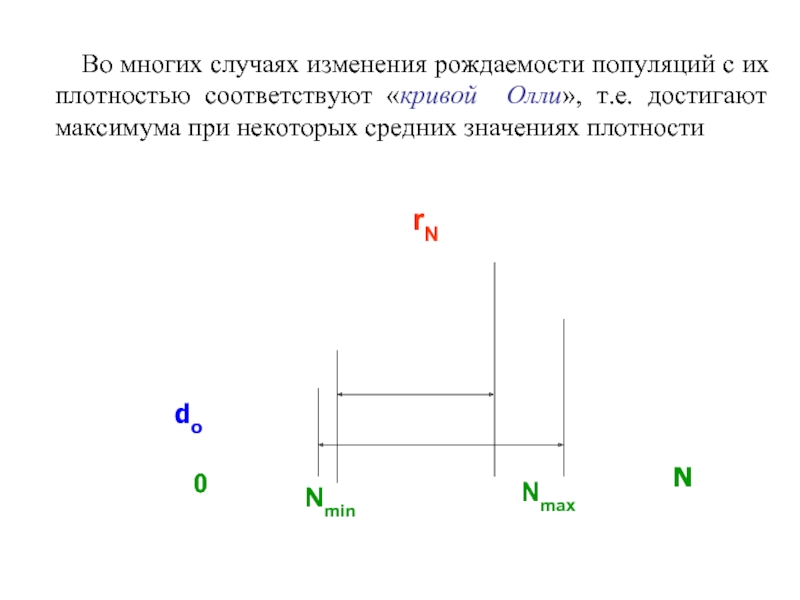
Слайд 51
do
Во многих случаях изменения рождаемости популяций с их плотностью
N
rN
Nmin
Nmax
0
Слайд 52 В таком случае существует не только максимальный (Nmax), но и минимальный
Nmin ≤ N ≤ Nmax.
Чем выше смертность в популяции, тем в более узких пределах будет изменяться ее численность.
Слайд 53 Рост численности популяций
Ростом популяции
При этом размеры, масса или возраст особей не имеют значения.
Перед рассмотрением количественных закономерностей роста популяций необходимо выделить следующие основные понятия.
Абсолютная скорость роста популяции (С), или прирост ее численности за (ΔN) за единицу времени (Δt), т.е.:
С =
Слайд 54 Значение имеет размерность [особи·время-1].
Когда значения Δt достаточно малы, абсолютный прирост характеризует мгновенную скорость роста популяции, т. е.
или первую производную численности по времени.
Слайд 55 Относительная скорость роста популяции (С’) определяется как
где N – средняя численность популяции за период Δt.
Значения С’ имеют размерность [время-1].
Когда Δt значения достаточно малы, получаем удельную скорость роста численности популяции (r):
_
_
Слайд 56 Удельную скорость роста популяции можно рассчитать
где N1 и N2 – численность популяции в моменты
времени t1 и t2.
Значения r имеют размерность [время-1].
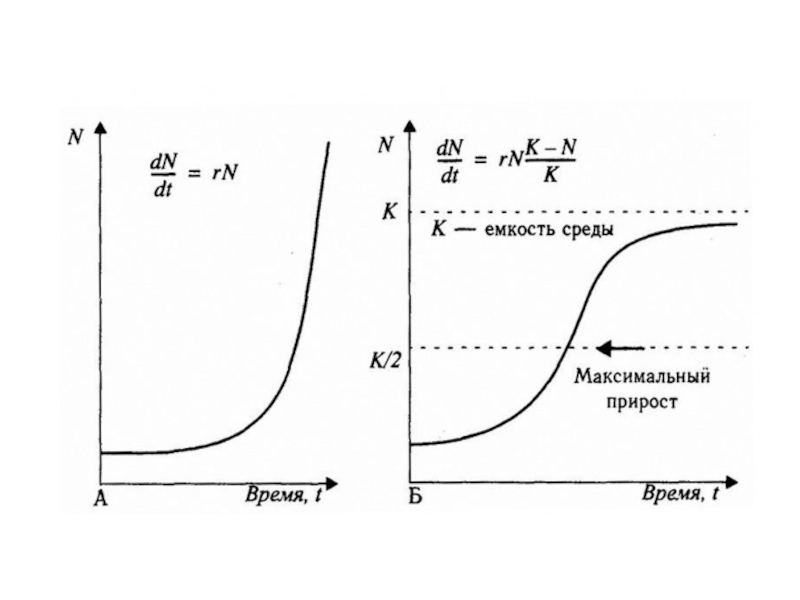
Если значения r в период времени t1 – t2 остаются постоянными, то рост численности популяции в этом интервале является экспоненциальным.
Слайд 57 В таком случае абсолютная скорость роста популяции
Исходя из
получаем:
,
Интегрированием последнего уравнения получаем уравнение экспоненциального роста:
Nt = Noert,
где No – начальная численность особей,
Nt – численность особей ко времени t.
Слайд 58 В полулогарифмических координатах график этого
lnNt = lnNo + rt
Слайд 59Примеры экспоненциального роста популяции от No = 10 экз при трех
r = 0,6
r = 0,4
r = 0,2
N, экз
Время, условные единицы
Слайд 60 Уравнение экспоненциально роста можно получить и другим
Если значения удельных скоростей рождаемости (b) и смертности (d) в популяции остаются постоянными, то:
Nt = Noebt - Noe-dt = Noe(b – d)t
Поскольку b и d - постоянные величины, их разность b - d = r представляет собой удельную скорость роста численности популяции.
Слайд 61 В природных условиях экспоненциальный рост встречается
Поэтому модель экспоненциального роста рассматривают в качестве оценки потенциальных возможностей увеличения численности популяции.
Слайд 63
Логистический рост численности популяции
В
Слайд 64
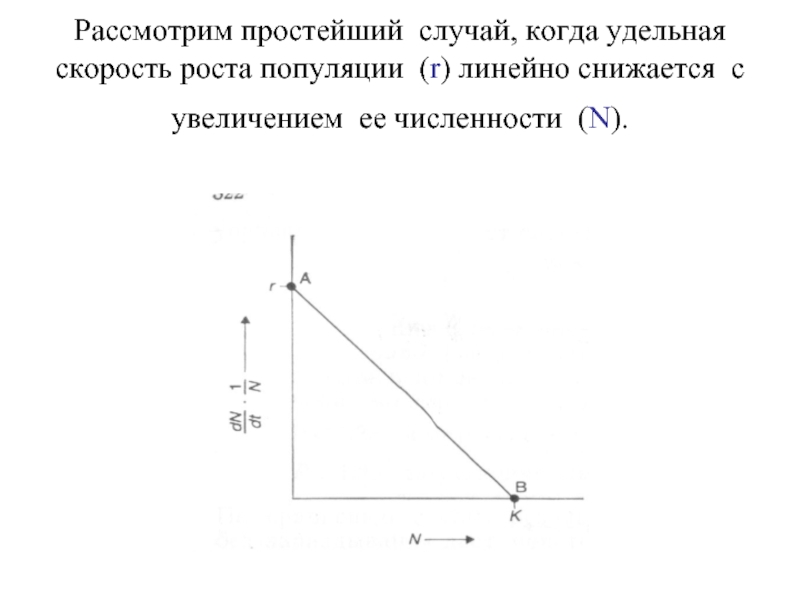
Рассмотрим простейший случай, когда удельная скорость роста популяции (r) линейно снижается
Слайд 65 Тогда связь между r и N выражается уравнением
rN = r - aN
где rN – удельная скорость роста популяции при плотности N,
r – ее максимальное значение при N, близкой к нулю,
а – эмпирический коэффициент.
При некоторой численности популяции (N = К) значение rN становится равным нулю. Тогда:
r – aK = 0, или a = r/K
Слайд 68
Преобразуем уравнение:
Получаем:
Значение
= Z является константой. Тогда:
- ZN2
Параметр ZN2
Слайд 69 При низких N («экологический вакуум»)
С повышением численности значения zN2 будут возрастать, поэтому рост численности будет замедляться и все более отличаться от экспоненциального.
При некотором значении N = K скорость роста популяции станет равной нулю, т.е. популяция достигнет своей максимальной численности (Nmax).
Слайд 70
Интегрирование уравнения
позволяет получить уравнение логистического роста:
где Nt – численность популяции
, где No – численность особей при t = 0.
Слайд 71 График логистического уравнения представляет S-образную кривую, асимптотически
Такой тип роста численности популяции называется логистическим ростом.
Слайд 73 t = 0 cуток, N = 12 особей;
Тогда
r = (ln20–ln12)/(2-0) = 0,2554 сут-1
Поскольку K = Nmax = 2133 особи, то
а = ln[(2133 – 12)/12] = 5,175
Тогда
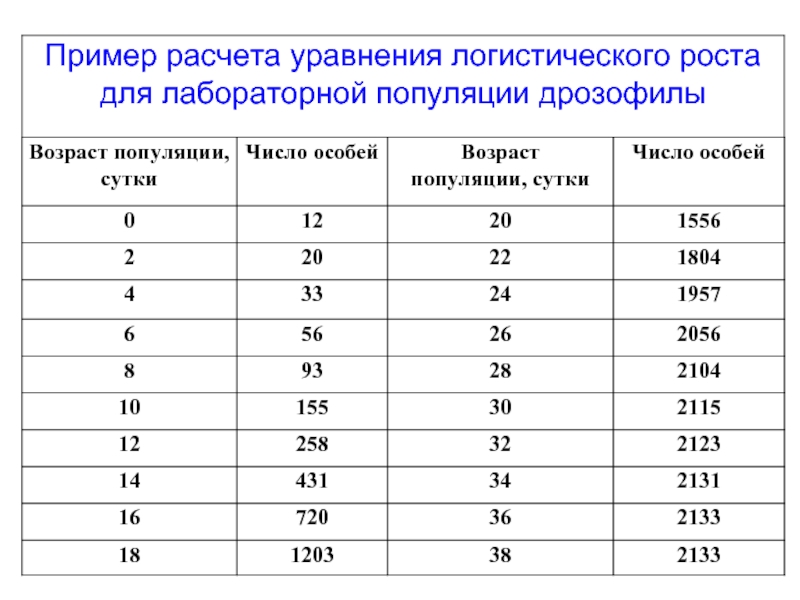
Слайд 74Рост численности популяции дрозофилы
Видно, что экспоненциальная
Слайд 75Емкость среды
Когда численность популяции
Емкость среды – способность природного окружения обеспечивать нормальную жизнедеятельность в единице пространства определенного числа особей определенной массы без заметного нарушения самого окружения.
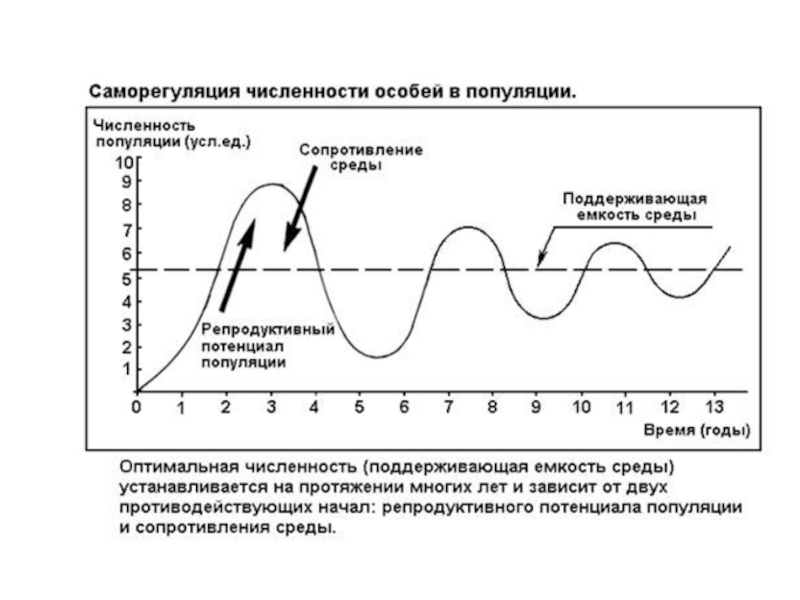
Слайд 76 Емкость среды проявляет свое действие через лимитирующие
Поддержание численности на определенном уровне происходит посредством механизмов отрицательной обратной связи.
















































![Значение имеет размерность [особи·время-1]. Когда значения Δt достаточно малы,](/img/tmb/2/161871/2830afee9439a55aaafc1f4b1a16c9c7-800x.jpg)