- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕХНОЛОГИИ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА презентация
Содержание
- 1. ТЕХНОЛОГИИ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА
- 2. Технологии ИИ Определения Формальная система (ФС) определяется
- 3. Технологии ИИ Определения Определение. Формальное доказательство –
- 4. Технологии ИИ Исчисление высказываний Примером ФС является
- 5. Технологии ИИ Множество ИВ Можно построить множество
- 6. Технологии ИИ ИВ и теория релейно-контактных схем
- 7. Технологии ИИ Язык предикатов первого порядка Операции
- 8. Технологии ИИ Правильно построенные формулы (ППФ) и
- 9. Технологии ИИ Принцип резолюции 1930 г. Эрбран.
- 10. Технологии ИИ Резольвенты Пусть имеется два конкретных
- 11. Технологии ИИ Алгоритм опровержения с помощью резолюций
- 12. Технологии ИИ Пример 1 Необходимо доказать, что
- 13. Технологии ИИ Пример 2 Описание: Любой студент,
- 14. Технологии ИИ Предикатная и дизъюнктивная формы Предположим,
- 15. Технологии ИИ Граф опровержения Граф опровержения разрешения
- 16. Технологии ИИ Резолюции в Прологе Пролог основан
- 17. Технологии ИИ Программа доказательства теорем на основе
- 18. Технологии ИИ Текст программы. Начало % Программа
- 19. Технологии ИИ Программа. Продолжение clauses %
- 20. Технологии ИИ Программа. Окончание % Вспомогательные предикаты
- 21. Технологии ИИ Пример с Сидоровым Исходные данные
- 22. Технологии ИИ Алгоритм унификации 1966, Ж.Питра и
- 23. Технологии ИИ Префиксная форма Eпреф=log + y
- 24. Технологии ИИ Идея алгоритма Eинф = cos2(a+1)+sin2(a+1) T = cos2(X)+sin2(X)->1
- 25. Технологии ИИ Программа унификации program UnifDemo; procedure
- 26. Технологии ИИ Программа. Продолжение function SUBST(var E1,
- 27. Технологии ИИ Программа. Продолжение function is_operator(c: char):
- 28. Технологии ИИ Программа. Продолжение function Unificate(E1, E2:
- 29. Технологии ИИ Программа. Продолжение type TTheoreme
- 30. Технологии ИИ Программа. Окончание begin Expr
- 31. Технологии ИИ Пример работы программы Expr: +-*ab*ab*1e
- 32. Технологии ИИ Системы автоматического доказательства теорем
- 33. Технологии ИИ Система Otter Программа автоматического
- 34. Технологии ИИ Как работает Otter Принцип постоянного
- 35. Технологии ИИ Алгоритм procedure Otter(sos, usable) inputs:
- 36. Технологии ИИ Расширение системы Prolog РТТР
- 37. Технологии ИИ
Слайд 2Технологии ИИ
Определения
Формальная система (ФС) определяется как четверка
ФС = {Σ, F, A,
Σ - конечный алфавит (конечное множество символов, словарь).
F - процедура построения формул (слов) формальной системы (грамматика формул). Можно трактовать как определение того, что такое формула.
A - конечное множество формул, называемых аксиомами.
P - конечное множество правил вывода, которые позволяют получать из некоторого конечного множества формул другое множество формул:
U1, U2,…,Un → W1, W2,…Wm
Ui, Wi – формулы ФС.
Слайд 3Технологии ИИ
Определения
Определение. Формальное доказательство – это конечная последовательность формул M1, M2,
Определение. Формула t называется теоремой, если существует доказательство, в котором она является последней:
Mr≡t
В частности, при таких определениях любая аксиома является теоремой.
Существует 2 типа правил вывода:
Продукции. Применяются к формулам, рассматриваемым как единое целое: tA→tAS
Правила переписывания. Применяются к любой отдельной части формулы: SS |→ S
Слайд 4Технологии ИИ
Исчисление высказываний
Примером ФС является исчисление высказываний (ИВ). ИВ – это
Алфавит ИВ:
Пропозициональные буквы p, q, r, s, t, …
Логические операторы ¬ (не), ⊃ (влечет, следует)
Скобки '(‘, ‘)’.
Построение формул ИВ:
Любая пропозициональная буква суть формула.
Если m-формула, то и (m) является формулой.
Если m-формула, то ¬m является формулой.
Если m1 и m2 – формулы, то m1 ⊃ m2 – формула.
Аксиомы ИВ:
(A1): m1 ⊃ (m2 ⊃ m1)
(A2): (m1 ⊃ (m2 ⊃ m3)) ⊃ ((m1 ⊃ m2) ⊃ (m1 ⊃ m3))
(A3): (¬m2 ⊃ ¬m1) ⊃ (m1 ⊃ m2)
Правила вывода:
m1 и (m1 ⊃ m2) |→ m2 (modus ponens или правило отделения)
В этой ФС 3 закона логики Аристотеля являются строго доказуемыми:
Закон тождества: (p ⊃ p)
Закон исключения третьего: (p∨¬p)
Закон противоречия: (¬ (p∧¬p))
Введение новых символов:
∧ (И): m1∧m2 ↔ ¬(¬m1⊃m2)
∨ (ИЛИ): m1∨m2 ↔ ¬(¬m1∧¬m2)
≡ (ТОЖДЕСТВО): m1≡m2 ↔ (m1⊃m2) ∧ (m2⊃m1)
Если истинно Φ и истинно, что из Φ следует Ψ, то Ψ также будет истинным.
«Каждый человек смертен. Сократ — человек. Следовательно, Сократ смертен». (modus Barbara, т.к. здесь имеются кванторы всеобщности).
Слайд 5Технологии ИИ
Множество ИВ
Можно построить множество различных систем аксиом ИВ. В том
Оператор - т.н. штрих Шеффера и одна аксиома.
Штрих Шеффера определяется следующим образом:
p | q ↔ (¬p) ∨ ( ¬q)
Аксиома Дж.Нико, 1916:
(A|(B|C)) | {[D | (D | D)] | [(E|B| ((A|E) | (A|E))]}
Слайд 6Технологии ИИ
ИВ и теория релейно-контактных схем
1910 г.: Пауль. С. Эренфест (1880-1933):
1938 г.: В. И. Шестаков (СССР), К. Шеннон (США) - строгое обоснование возможности использования исчисления высказывании для описания релейно-контактных схем.
1950 г., монография М.А. Гаврилова (1903-1979) "Теория релейно-контактных схем" .
Слайд 7Технологии ИИ
Язык предикатов первого порядка
Операции с высказываниями, расчлененными на субъекты и
Алфавит языка предикатов первого порядка включает в себя:
разделители
константы
переменные
предикаты
функции
логические операторы (¬, ∧, ∨, →, ↔)
кванторы (∃, ∀)
Предикат (логическая функция) – это функция от любого числа аргументов, принимающая значения Истина и Ложь.
Терм – выражение, включающее константы, переменные и функции.
В исчислении предикатов 1-го порядка запрещено квантифицировать символы предикатов и функций.
К аксиомам логики предикатов добавляются:
∀ x F(x) → F(y)
F(y) → ∃x F(x)
Слайд 8Технологии ИИ
Правильно построенные формулы (ППФ) и предложения
Правильно построенная формула (ППФ)
всякий атом
если G и H – ППФ, а X – переменная, то (¬H), (G∧H), (G∨H), (∃X)G, (∀X)H – ППФ.
Предложение – формула, представляющая собой дизъюнкцию литералов
Преобразование ППФ в предложения
Исключение символов эквивалентности и импликации F ↔ G ≡ (F→G) ∧ (G→F) F → G ≡ ¬F∨G
Уменьшение области действия знаков отрицания. Отрицание должно быть применено не более, чем к одному атому. ¬(F∨G) ≡ ¬F∧¬G
Разделение переменных. Каждый квантор должен иметь только свою, свойственную ему, переменную.
Исключение кванторов существования Например, пусть имеем (∀ X)(∃ Y) P(X,Y) Видимо, Y зависит от X, т.е. Y=g(X) (т.н. функция Сколема или сколемовская функция). Тогда можно записать: (∀ X)P(X,g(X))
Слайд 9Технологии ИИ
Принцип резолюции
1930 г. Эрбран. Метод доказательства теорем в ФС первого
Идея: чтобы получить некоторое заключение C, исходя из гипотез H1, H2,…Hn, т.е. доказать теорему T:
H1 ∧ H2 ∧ Hn ⊃ C,
достаточно доказать противоречивость формулы F:
H1 ∧ H2 ∧ Hn ∧ ¬ C,
в которой отрицание заключения добавлено к исходным гипотезам. Это может оказаться проще прямого вывода.
Соображения тривиальны: доказательство выполнимости множества G→H (¬G∨H) – это опровержение его невыполнимости, т.е. невыполнимости ¬(¬G∨H), что эквивалентно G∧¬H.
Установление невыполнимости множества предложений осуществляется посредством принципа резолюций – специальной процедуры логического вывода новых предложений из множества исходных.
Слайд 10Технологии ИИ
Резольвенты
Пусть имеется два конкретных (не содержащих переменных) предложения
P1∨P2∨…∨Pn и ¬P1∨Q1∨…∨Qm
Из
Очевидно, что принцип резолюций покрывает правило вывода modus ponens.
Пример. Пусть имеется пара предложений
¬P∨R и ¬R∨Q (или P→R, R→Q)
Резольвентой этих предложений является ¬P ∨ Q (или P→Q). Это правило вывода называется сцеплением.
Для обобщения этого правила на случай предложений, содержащих переменные, используется специальная процедура, называемая унификацией.
Пусть имеется пара
¬F(X)∨G(X) и F(f(Y))
Если первое предложение заменить на
¬F(f(Y))∨G(f(Y)), то получим резольвенту G(f(Y)).
Унификация заключается в замене переменных с целью появления дополнительных литералов.
Слайд 11Технологии ИИ
Алгоритм опровержения с помощью резолюций
Предположим, что целью алгоритма резолюций является
G→H.
Резолюция(G,H)
1. Сформировать C – множество предложений, полученных путем преобразования формул множества G.
2. Добавить к множеству C предложения, полученные из ¬H.
3. Пока в C не появится пустое предложение выполнять:
3.1. Выбрать 2 различных предложения S1 и S2 из C.
3.2. Если они имеют резольвенту R, то добавить эту резольвенту к множеству C.
Конец цикла
Конец алгоритма.
В этой процедуре требуется предварительное приведение исходных предложений к дизъюнктивной нормальной форме.
Слайд 12Технологии ИИ
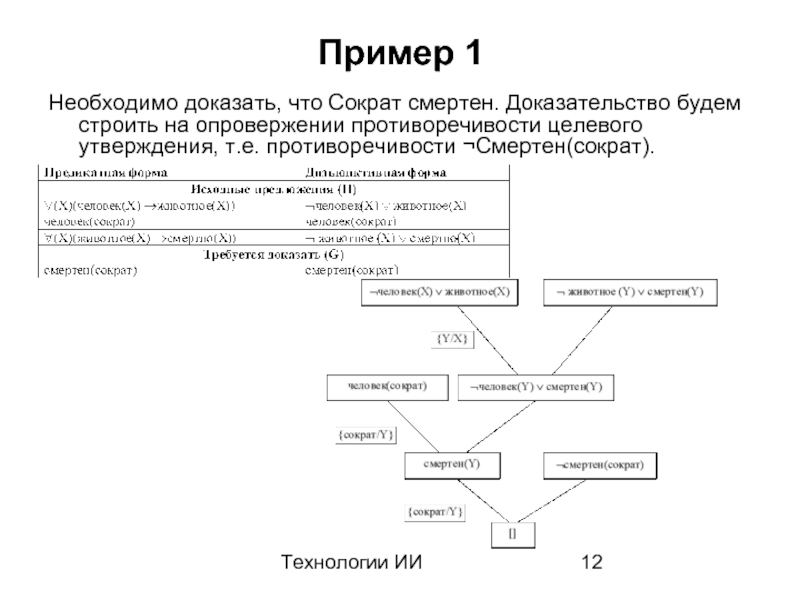
Пример 1
Необходимо доказать, что Сократ смертен. Доказательство будем строить на
Слайд 13Технологии ИИ
Пример 2
Описание: Любой студент, который сдает экзамен по физике и
Вопрос: счастлив ли Сидоров?
Слайд 14Технологии ИИ
Предикатная и дизъюнктивная формы
Предположим, что мы хотим доказать, что Сидоров
¬happy(сидоров).
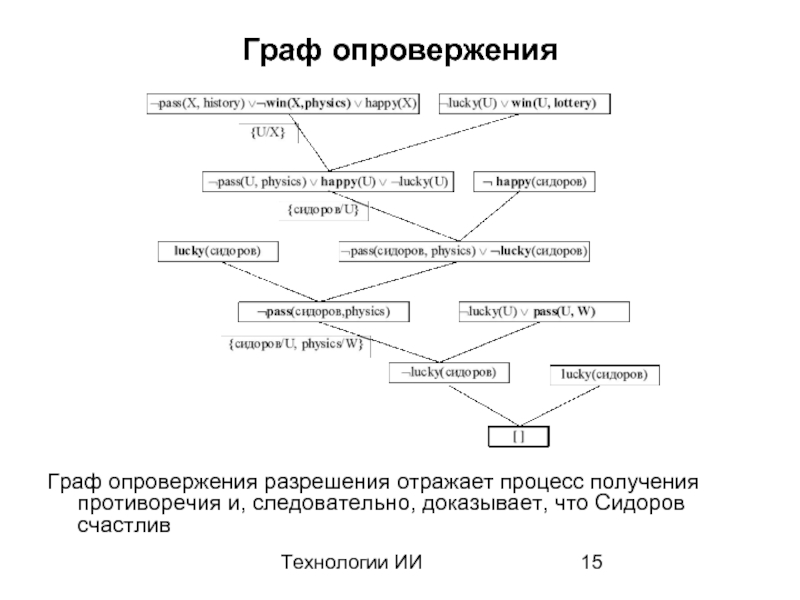
Слайд 15Технологии ИИ
Граф опровержения
Граф опровержения разрешения отражает процесс получения противоречия и, следовательно,
Слайд 16Технологии ИИ
Резолюции в Прологе
Пролог основан на логике предикатов первого порядка. В
¬P1∨¬P2∨…∨¬Pn ∨ Pm
или
P1∧P2∧…∧Pn → Pm
При этом:
резолюция использует первый отрицательный литерал слева направо в центральном предложении
резолюции выполняются в глубину, т.е. полученная резольвента тут же участвует в следующей резолюции.
Слайд 17Технологии ИИ
Программа доказательства теорем на основе принципа резолюций
Описание исходных предложений:
(¬a ∨
sent([t(0,"a"),t(1,"b")]). -- (¬a ∨ b)
sent([t(0,"b"),t(1,"c")]). -- (¬b ∨ c)
sent([t(1,"a")]). -- a
sent([t(0,"c")]). -- ¬c
Здесь 0 - отрицание, 1 - прямая форма
Шаг резолюции состоит из следующих действий:
Берутся 2 предложения в ДНФ D1 и D2.
Ищутся дизъюнкты P в D1 и ¬P в D2. Если таковые найдены, то формируется дизъюнкция этих предложений с исключение P и ¬P.
Полученная резольвента добавляется в базу (множество предложений).
Слайд 18Технологии ИИ
Текст программы. Начало
% Программа доказательства теорем на основе принципа резолюций
domains
t2(integer, symbol, symbol);
t3(integer, symbol, symbol, symbol)
tlist = term * % список термов
predicates
start
compare(term, term)
end(tlist)
resolstep(tlist, tlist, tlist)
unify(symbol, symbol)
isvar(symbol)
isconst(symbol)
% Соединение двух списков (деление списка на 2 части)
a2(tlist, tlist, tlist)
% Выбор очередного элемента из списка
eget(tlist, term) % (i,o)
% Удаление элемента из списка
remove(tlist, term, tlist) % (i,i,o)
database
sent(tlist)
goal
% Загружаем предложения
retractall(_),
consult("resol.db"),
start.
Слайд 19Технологии ИИ
Программа. Продолжение
clauses
% Запуск программы
start:-
sent(C1),
sent(C2),
not(end(C1vC2)),
% Добавляем резольвенту
asserta(sent(C1vC2)), !,
start.
% Шаг резолюции. На входе - предложения С1 и С2. Далее
% из них выделяются дизъюнкты E1 и E2. Дизъюнкты
% сопоставляются и, в случае обнаружения соответствия
% вида (~P и P), формируется резольвента CAvCB. Результат заносится в БД.
resolstep(C1, C2, CAvCB):-
% извлекаем из С1 и C2 элементы E1 и E2
eget(C1, E1), eget(C2, E2),
write(" E1=",E1, ", E2=",E2,"\n"),
% далее сопоставляем подвыражения
compare(E1, E2),
% удаляем подвыражение E1 из С1 и E2 из С2
remove(C1, E1, CA),
remove(C2, E2, CB),
% склеиваем списки, полученные после удаления из них P и ~P
a2(CA, CB, CAvCB), !.
% Проверка на P и ~P - поиск резольвенты
compare(t(N1,X1), t(N2,X2)) :- N1+N2 = 1, unify(X1, X2).
compare(t2(N1,NAME,ARG1), t2(N2,NAME,ARG2)) :- N1+N2 = 1, unify(ARG1, ARG2).
compare(t3(N1,NAME,ARG11,ARG12), t3(N2,NAME,ARG21, ARG22)) :-
N1+N2 = 1,
unify(ARG11, ARG21),
unify(ARG12, ARG22).
% Если список пуст, значит есть противоречие
end([]):- write("\n\nОбнаружено противоречие. Теорема доказана.\n"), exit(0).
% Проверка на унифицируемость
unify(A, A) :- !.
unify(A, B) :- isvar(A), isvar(B), !.
unify(A, B) :- isvar(A), isconst(B), !.
unify(A, B) :- isconst(A), isvar(B), !.
isvar(S) :- frontchar(S,Ch,_), Ch>='A', Ch<='Z', !.
isconst(S) :- frontchar(S,Ch,_), Ch>='a', Ch<='z', !.
Слайд 20Технологии ИИ
Программа. Окончание
% Вспомогательные предикаты
a2([], L, L).
a2([Head | L1], L2,
eget([H|T],H).
eget([_|T],R) :- eget(T,R).
remove(L, El, Res) :-
a2(L1,[El|L2],L),
a2(L1,L2,Res).
Слайд 21Технологии ИИ
Пример с Сидоровым
Исходные данные (файл resol.db) :
sent([t2(0,"lucky","U"),t3(1,"win","U","lottery")]).
¬lucky(U)
sent([t2(0,"lucky","Y"),t3(1,"pass","Y","Z")]). ¬lucky(Y) ∨ pass(Y,Z).
sent([t2(0,"study","Y"),t3(1,"pass","Y","Z")]). ¬study(Y) ∨ pass(Y,Z).
sent([t2(0,"study","sidorov")]). ¬study(сидоров)
sent([t3(0,"pass","X",“physics"),t3(0,"win","X","lottery"),t2(1,"happy","X")]). -- ¬pass(X, physics) ∨ ¬win(X,lottery) ∨ happy(X).
sent([t2(1,"lucky","sidorov")]). lucky(сидоров).
sent([t2(0,"happy","sidorov")]). ¬happy(сидоров)
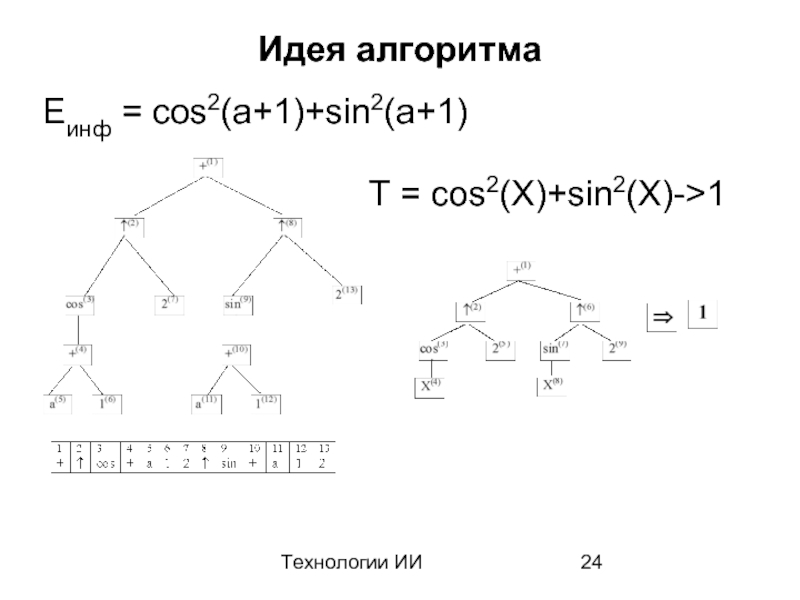
Слайд 22Технологии ИИ
Алгоритм унификации
1966, Ж.Питра и (независимо от него) Дж.Робинсон на основе
Основной объект - терм.
Терм – n-арный объект вместе с n термами.
Должны существовать априори исходные термы, являющиеся объектами.
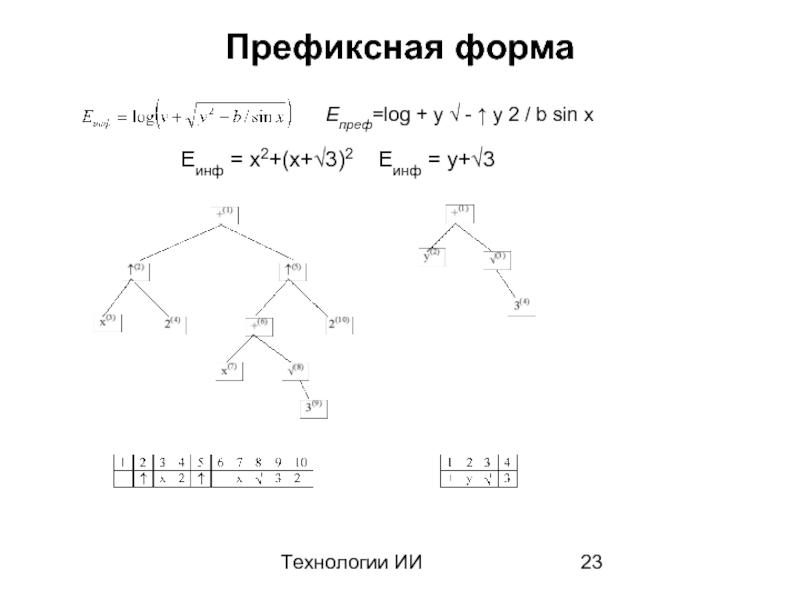
Слайд 25Технологии ИИ
Программа унификации
program UnifDemo;
procedure replace(var S: string; n: integer; v: string);
begin
Insert(v, S, n);
end;
type
TVarN = record
Name, Val: string;
end;
const
MaxVar = 100;
var
VarNum : integer;
VarList: array[1..MaxVar] of TVarN;
function AddVar(v: char; t: string): boolean;
var i:integer;
begin
AddVar := false;
for i:=1 to VarNum do
begin
if VarList[i].Name = v then
if VarList[i].Val = t then AddVar := true;
exit;
end;
VarNum := VarNum+1;
if VarNum>MaxVar then error('too many vars');
VarList[VarNum].Name := v;
VarList[VarNum].Val := t;
AddVar := true;
end;
Слайд 26Технологии ИИ
Программа. Продолжение
function SUBST(var E1, E2: string; v: char; t: string;
{ v - свободная переменная, t - терм,
h1 - индекс в выражении E1,
h2 - индекс в выражении E2}
var i: integer;
begin
SUBST := false;
{ Просмотр терма t на предмет поиска недопустимых в нем переменных}
for i:=1 to length(t) do
if t[i]=v then exit;
{ Просмотр E1 }
i:=h1;
while i<=length(E1) do
begin
if E1[i]=v then
replace(E1, i, t); {замена символа термом}
if not AddVar(v,t) then exit;
i:=i+1;
end;
{ Просмотр E2 }
i := h2;
while i<=length(E2) do
begin
if E2[i]=v then
replace(E2, i, t); {замена символа термом}
if not AddVar(v,t) then exit;
i:=i+1;
end;
SUBST := true;
end;
Слайд 27Технологии ИИ
Программа. Продолжение
function is_operator(c: char): boolean;
Begin is_operator := (c in['+','-','*','/','\','~','^','&','|','=']);
function is_constant(c: char): boolean;
Begin is_constant := (c in['a'..'z']) or (c in['0'..'9']); end;
function is_var(c: char): boolean;
Begin is_var := (c in['A'..'Z']); end;
function getterm(E: string; n: integer): string;
var
t: string;
i: integer;
cnt: integer;
eoj: boolean;
begin
t := '';
cnt := 1;
i := n;
eoj := false;
while not eoj do
begin
t := t+E[i];
if is_operator(E[i]) then
cnt:=cnt+1
else
cnt := cnt-1;
i := i+1;
eoj:= (i>length(E)) or (cnt=0);
end;
getterm := t;
end;
Слайд 28Технологии ИИ
Программа. Продолжение
function Unificate(E1, E2: string) : boolean;
{ E1, E2 -
var
h1, h2: integer;
t: string;
begin
Unificate := false;
h1 := 1; { начальное выражение - символ из E1 }
h2 := 1; { начальное_выражение - символ из E2 }
{ Просмотреть параллельно Expr1 и Expr2 }
VarNum := 0;
while h2<=length(E2) do
begin
if E1[h1]<>E2[h2] then
begin
//Константы не совпали
if is_constant(E1[h1]) and is_constant(E2[h2]) then exit;
if is_operator(E1[h1]) then // оператор
begin
if is_operator(E2[h2]) then exit;
if is_var(E2[h2]) then // E2[h2] - переменная
begin
// Пробуем заменить оператор на терм. t - терм-дебютант из E1
t := getterm(E1,h1);
if not SUBST(E1, E2, E2[h2], t, h1, h2) then exit;
end
end
else // E1(h1) - переменная
begin
if is_var(E2[h2]) then // E2[h2] - переменная
begin
// Пробуем заменить переменную на другую переменную
if not SUBST(E1, E2, E2[h2], E1[h1], h1, h2) then exit;
end
else
begin
// Пробуем заменить переменную на терм
// t - терм-дебютант из E2
t := getterm(E2,h2);
if not SUBST(E1, E2, E1[h1], t, h1, h2) then exit;
end
end;
end;
h1 := h1+1;
h2 := h2+1;
end;
Unificate := (E1=E2);
end;
Слайд 29Технологии ИИ
Программа. Продолжение
type
TTheoreme = record
{ T - теорема
H, C: string; {H(гипотеза) -> C(заключение)}
end;
const
Tnum = 6;
TT:array[1..Tnum] of TTheoreme =
((H:'-XX';C:'0'),
(H:'+0X';C:'X'),
(H:'+X0';C:'X'),
(H:'*X1';C:'X'),
(H:'*1X';C:'X'),
(H:'/X1';C:'X'));
var
Expr: string;
res : boolean;
t: string;
i, n, k: integer;
Cons: string;
Слайд 30Технологии ИИ
Программа. Окончание
begin
Expr := '+-*ab*ab*1e'; {E=2*a-2*a}
i := 1;
while
begin
if is_operator(Expr[i]) then
begin
t := getterm(Expr,i);
{Проходим по всему списку теорем}
for n:=1 to Tnum do
begin
res := Unificate(t, TT[n].H);
if res then
begin
Cons := TT[n].C;
{Подставляем значения переменных}
for k:=1 to VarNum do
SUBST(Cons, Cons, VarList[k].Name[1], VarList[k].Val,1,1);
delete(Expr, i, length(t));
Insert(Cons, Expr, i);
write('( "',t,'" with "',TT[n].H,'" -> "',Cons,'") -> ');
writeln(Expr);
i:=0;
end;
end;
end;
i:=i+1;
end;
writeln('Result: ',Expr);
end.
Слайд 31Технологии ИИ
Пример работы программы
Expr: +-*ab*ab*1e
( "-*ab*ab" with "-XX" -> "0") ->
( "+0*1e" with "+0X" -> "*1e") -> *1e
( "*1e" with "*1X" -> "e") -> e
Result: e
Слайд 32Технологии ИИ
Системы автоматического доказательства теорем
Отличие систем автоматического доказательства теорем (или
обычно поддерживают полную логику первого порядка;
синтаксическая форма, выбранная для высказываний, не влияет на результаты;
управляющая информация обычно хранится отдельно от БЗ, а не входит в состав самого представления знаний
большинство исследований в области САД посвящено поиску стратегий управления, которые приводят к общему повышению эффективности, а не только к увеличению быстродействия.
Слайд 33Технологии ИИ
Система Otter
Программа автоматического доказательства теорем Otter (Organized Techniques for
Подготавливая любую задачу для программы Otter, пользователь должен разделить знания на четыре части:
Множество выражений, известное как множество поддержки, в котором определяются важные факты о данной задаче. На каждом этапе резолюции операция резолюции применяется к одному из элементов множества поддержки и к другой аксиоме, поэтому поиск сосредоточивается на множестве поддержки.
Множество полезных аксиом (usable axiom), которое выходит за пределы множества поддержки. Эти аксиомы предоставляют фоновые знания о проблемной области.
Множество уравнений, известных как правила перезаписи (rewrites), или демодуляторы (demodulators). Демодуляторы представляют собой уравнения. Например:
х+0=х (любой терм в форме х+0 должен быть заменен термом х).
Множество параметров и выражений, которое определяет стратегию управления. В частности - задание эвристической функции для управления поиском и функцию фильтрации для устранения некоторых подцелей как не представляющих интереса.
Слайд 34Технологии ИИ
Как работает Otter
Принцип постоянного применения правила резолюции к одному из
В отличие от системы Prolog, в этой программе используется определенная форма поиска по первому наилучшему совпадению. Ее эвристическая функция измеряет "вес" каждого выражения с учетом того, что наиболее предпочтительными являются выражения с наименьшими весами. Единичные выражения оцениваются как имеющие наименьший вес.
На каждом этапе программа Otter перемещает выражение "с наименьшим весом" из множества поддержки в список полезных аксиом и добавляет в множество поддержки некоторые непосредственные следствия применения операции резолюции к выражению с наименьшим весом и к элементам списка полезных аксиом.
Программа Otter останавливается, если обнаруживает противоречие или если возникает такая ситуация, что в множестве поддержки не остается больше выражений.
Слайд 35Технологии ИИ
Алгоритм
procedure Otter(sos, usable)
inputs:
sos -- множество поддержки – выражения, определяющие
-- решаемую задачу
usable -- множество фоновых значений, которые потенциально -- могут быть релевантными для данной задачи
repeat
clause ← элемент множества sos с наименьшим весом;
переместить выражение clause из множества sos в множество usable;
Process(Infer(clause, usable), sos)
until sos=[] or <обнаружится опровержение>
function Infer(clause, usable) returns множество выражений clauses
применить правило резолюции к выражению clause и каждому элементу множества usable;
возвратить полученное множество clauses после применения функции Filter
procedure Process(clauses, sos)
for each clause in clauses do
clause ← Simplify(clause)
выполнить слияние идентичных литералов;
отбросить выражение clause, если оно представляет собой тавтологию
sos ← [clause | sos]
if clause не имеет литералов, то обнаружено опровержение
if clause имеет один литерал, то искать единичное опровержение
Слайд 36Технологии ИИ
Расширение системы Prolog
РТТР (Prolog Technology Theorem Prover).
1. В процедуру
2. Поиск в глубину заменяется поиском с итеративным углублением. Это позволяет добиться того, чтобы стратегия поиска стала полной, а увеличение продолжительности поиска измерялось лишь постоянной зависимостью от времени.
3. Разрешается применение отрицаемых литералов (таких как ¬P(x)). В этой реализации имеется две отдельные процедуры; в одной из них предпринимается попытка доказать Р, а в другой — доказать ¬P
4. Выражение с n атомами хранится в виде n различных правил. Например, при наличии в базе знаний выражения A ⇐ B ∧ C должно быть также предусмотрено хранение в ней этого выражения, представленного как ¬B ⇐ C ∧ ¬A и как ¬C ⇐ B ∧ ¬A.
5. Логический вывод сделан полным (даже для нехорновских выражений) путем добавления правила резолюции с линейным входным выражением: если текущая цель унифицируется с отрицанием одной из целей в стеке, то данная цель может рассматриваться как решенная (один из способов рассуждения от противного). Если первоначальной целью было высказывание Ρ и эта цель свелась в результате вывода к цели ¬P, то установлено, что ¬P⇒P. А это выражение логически эквивалентно Р.

















![Технологии ИИПрограмма. Окончание% Вспомогательные предикатыa2([], L, L). a2([Head | L1], L2, [Head | L3]) :-](/img/tmb/1/23965/02c3fcc3f24ca5d2c3f646414278eb65-800x.jpg)




![Технологии ИИПрограмма. Продолжениеfunction is_operator(c: char): boolean;Begin is_operator := (c in['+','-','*','/','\','~','^','&','|','=']); end;function is_constant(c: char): boolean;Begin is_constant](/img/tmb/1/23965/15ab54b600d694f3a5dd812864716a82-800x.jpg)



 "0") -> +0*1e( "+0*1e" with "+0X"" alt="">
"0") -> +0*1e( "+0*1e" with "+0X"" alt="">










