Ю. А. Скобцов, д. т. н., профессор
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимизация раскроя рулонного металлопроката на слиттере презентация
Содержание
- 1. Оптимизация раскроя рулонного металлопроката на слиттере
- 2. Рулонные материалы металл бумага ткани пленки пластик
- 3. Рулонный металлопрокат Масса рулонов от 5 до
- 4. Продольные полосы используются: в прокатном производстве (электросварные
- 5. Технология раскроя на слиттерах Схема слиттерной линии:
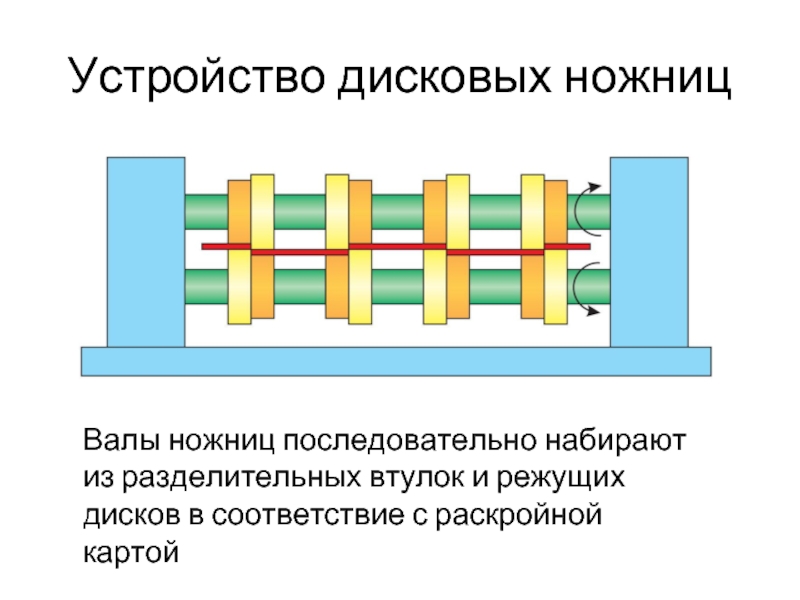
- 6. Устройство дисковых ножниц Валы ножниц последовательно набирают
- 7. Параметры слиттерных линий: максимальная масса раскраиваемого рулона
- 8. Производители слиттерных линий: Украина: «Финпрофиль» (Печенеги, Харьковская
- 9. Решение раскройной задачи Классифицировать задачу Изучить имеющийся
- 10. Задачи рационального раскроя Изучением таких задач занимается
- 11. История вопроса (1) Работа Л.В. Канторовича «Математические
- 12. История вопроса (2) 2. Gilmore & Gomory
- 13. История вопроса (3) 3. Типология Dychhoff: A
- 14. Классификация изучаемой задачи Сравним с одно- и
- 15. Классическая 1-мерная задача Минимизируется расход по длине L1, ширина B1 не учитывается
- 16. Продольный раскрой на полосы Минимизируется расход по
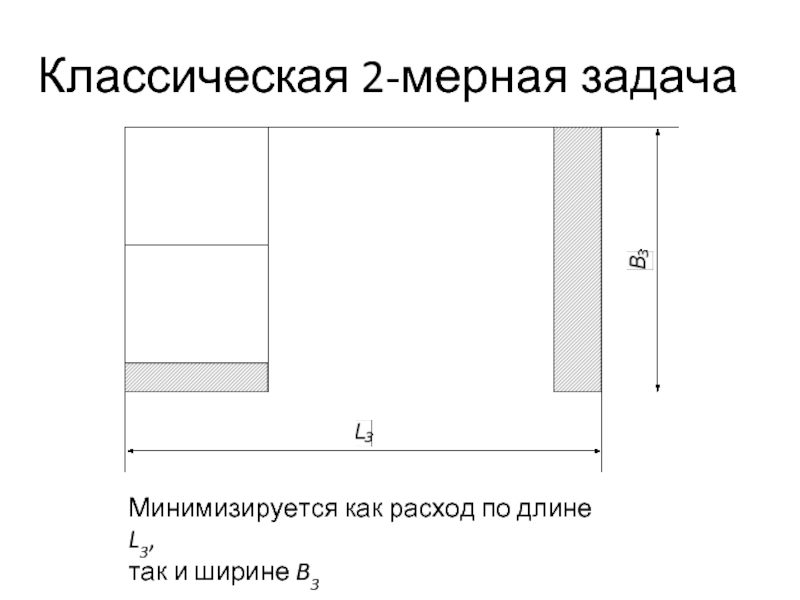
- 17. Классическая 2-мерная задача Минимизируется как расход по длине L3, так и ширине B3
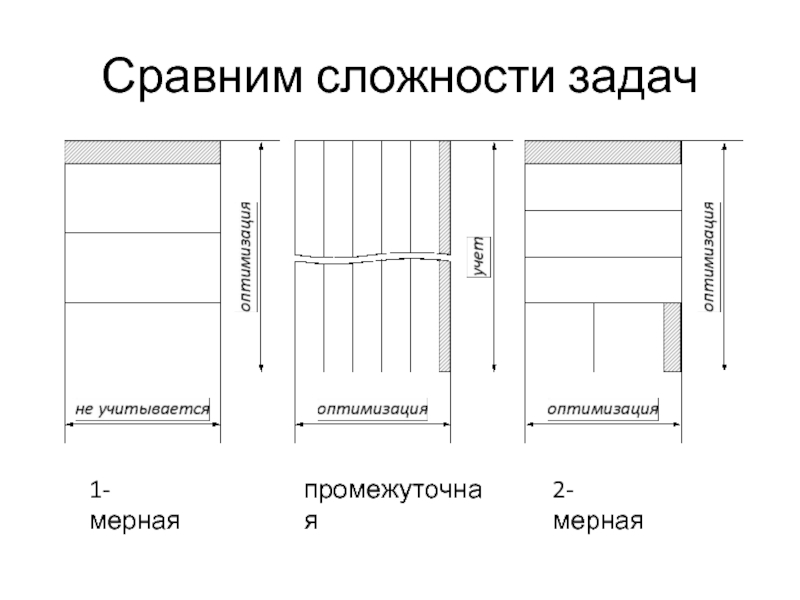
- 18. Сравним сложности задач 1-мерная 2-мерная промежуточная
- 19. 1,5-мерная раскройная задача промежуточная по сложности между
- 20. Методы решения задачи эвристические (линейное программирование, последовательные
- 21. Далее предполагается: программная реализация двух метаэвристик последующее
- 22. Спасибо за внимание! В. Н. Балабанов Ю. А. Скобцов akavrt@gmail.com skobtsov@kita.dgtu.donetsk.ua → → Связь:
Рулонные материалы металл бумага ткани пленки пластик
Слайд 1«Оптимизация раскроя рулонного металлопроката на слиттере»
Доклад
Кто?
В. Н. Балабанов, аспирант
Откуда?
ДонНТУ,
кафедра АСУ
Слайд 3Рулонный металлопрокат
Масса рулонов
от 5 до 30 тонн
Различные виды покрытия
Ширина полосы
до 2
метров
Толщина полосы
от 0,2 до 10 мм
Толщина полосы
от 0,2 до 10 мм
Слайд 4Продольные полосы используются:
в прокатном производстве (электросварные трубы, профиль)
в штамповочном производстве (заготовки)
в
деревообрабатывающей промышленности (упаковочный материал, лента)
в строительстве (кровельный материал)
в производстве кабельной продукции (защитный материал для бронирования)
в строительстве (кровельный материал)
в производстве кабельной продукции (защитный материал для бронирования)
Слайд 5Технология раскроя на слиттерах
Схема слиттерной линии:
1 — разматыватель; 2 — правильная
машина; 3 — дисковые ножницы;
4 — петлеобразователь; 5 — натяжное устройство; 6 —наматыватель
4 — петлеобразователь; 5 — натяжное устройство; 6 —наматыватель
Слайд 6Устройство дисковых ножниц
Валы ножниц последовательно набирают из разделительных втулок и режущих
дисков в соответствие с раскройной картой
Слайд 7Параметры слиттерных линий:
максимальная масса раскраиваемого рулона
ширина и толщина раскраиваемой ленты
минимальная ширина
получаемого штрипса (узкой стальной полосы)
скорость подачи ленты
суммарная мощность реза
наличие узла поперечной резки
скорость подачи ленты
суммарная мощность реза
наличие узла поперечной резки
Слайд 8Производители слиттерных линий:
Украина: «Финпрофиль» (Печенеги, Харьковская обл.), завод «Эверкон» (Чугуев, Харьковская
обл.), инжиниринговая группа «Стан-Групп» (Киев)
Россия: НИИ МИТОМ (Ульяновск), «Феррум-Строй» (Калининград), «Аркада-Инжиниринг» (Смоленск), «ТПК Расенич» (Москва), «НЗПО» (Новолипецк), «Ремпрессмаш» (Москва)
Беларусь: «АМТинжиниринг»
Россия: НИИ МИТОМ (Ульяновск), «Феррум-Строй» (Калининград), «Аркада-Инжиниринг» (Смоленск), «ТПК Расенич» (Москва), «НЗПО» (Новолипецк), «Ремпрессмаш» (Москва)
Беларусь: «АМТинжиниринг»
Слайд 9Решение раскройной задачи
Классифицировать задачу
Изучить имеющийся опыт
Выбрать метод решения
Разработать систему
Внедрить в производство
Слайд 10Задачи рационального раскроя
Изучением таких задач занимается дисциплина исследования операций (Operational Research)
Родственные
задачи: задачи рациональной упаковки, задача о ранце и т.д.
Являются NP-сложными задачами комбинаторной оптимизации
Являются NP-сложными задачами комбинаторной оптимизации
Слайд 11История вопроса (1)
Работа Л.В. Канторовича «Математические методы в организации и планировании
производства» (1939).
«Задача формирования такого плана раскроя, который в серийном производстве дал бы минимальный расход материала в среднем на один комплект заготовок.»
«Задача формирования такого плана раскроя, который в серийном производстве дал бы минимальный расход материала в среднем на один комплект заготовок.»
Слайд 12История вопроса (2)
2. Gilmore & Gomory в работах:
A linear programming approach
to cutting-stock problem (1961)
A linear programming approach to cutting-stock problem. Part II (1963)
Multistage cutting stock problems of two and more dimensions (1965)
A linear programming approach to cutting-stock problem. Part II (1963)
Multistage cutting stock problems of two and more dimensions (1965)
Слайд 13История вопроса (3)
3. Типология Dychhoff:
A typology of cutting and packing problems
(1990)
4. Улучшенная типология Wäscher:
An improved typology of cutting and packing problems (2007)
4. Улучшенная типология Wäscher:
An improved typology of cutting and packing problems (2007)
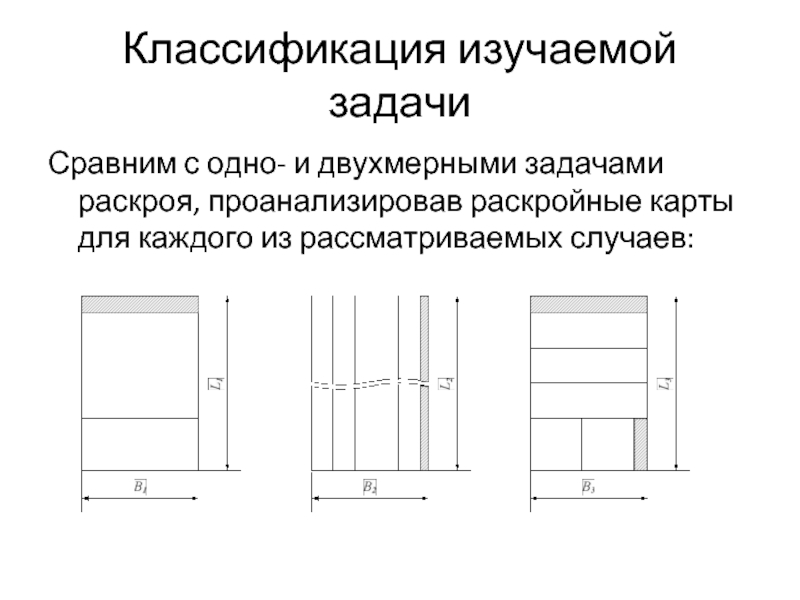
Слайд 14Классификация изучаемой задачи
Сравним с одно- и двухмерными задачами раскроя, проанализировав раскройные
карты для каждого из рассматриваемых случаев:
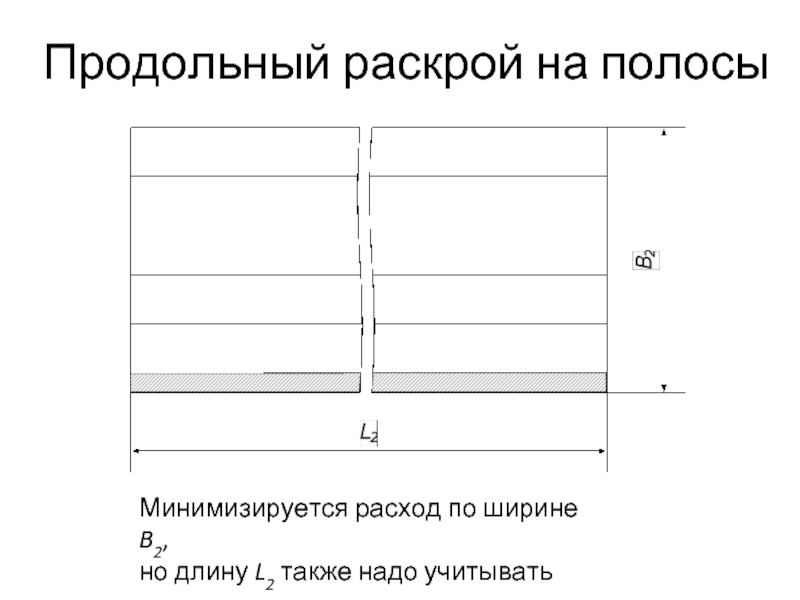
Слайд 16Продольный раскрой на полосы
Минимизируется расход по ширине B2,
но длину L2
также надо учитывать
Слайд 191,5-мерная раскройная задача
промежуточная по сложности между одно- и двухмерными задачами рационального
раскроя
понятие ввел Haessler в работе:
A procedure for solving the 1.5-dimensional coil slitting problem (1978)
получило распространение
в типологиях отдельно не рассматривается
понятие ввел Haessler в работе:
A procedure for solving the 1.5-dimensional coil slitting problem (1978)
получило распространение
в типологиях отдельно не рассматривается
Слайд 20Методы решения задачи
эвристические (линейное программирование, последовательные эвристические процедуры, гибридные методы)
метаэвристические (поиск
с запретами, имитация отжига, GRASP, методы эволюционных вычислений, метод муравьиных колоний, PSO)
алгоритмические (линейные и степенные преобразования, переборные методы)
алгоритмические (линейные и степенные преобразования, переборные методы)
Слайд 21Далее предполагается:
программная реализация двух метаэвристик
последующее сравнении эффективности
модификация для учета технологических особенностей
1,5-мерного раскроя
тестирование и внедрение системы на Донецком металлургическом заводе в цехе тонкостенных труб и металлической мебели (ЦТТММ) для оптимизации продольного раскроя рулонного металлопроката при производстве прямошовных электросварных труб и профиля
тестирование и внедрение системы на Донецком металлургическом заводе в цехе тонкостенных труб и металлической мебели (ЦТТММ) для оптимизации продольного раскроя рулонного металлопроката при производстве прямошовных электросварных труб и профиля
Слайд 22Спасибо за внимание!
В. Н. Балабанов
Ю. А. Скобцов
akavrt@gmail.com
skobtsov@kita.dgtu.donetsk.ua
→
→
Связь:
