Скрынник Дарья
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методические подходы к подготовке учащихся 5–8 классов к участию в математических конкурсах и олимпиадах презентация
Содержание
- 1. Методические подходы к подготовке учащихся 5–8 классов к участию в математических конкурсах и олимпиадах
- 2. ДИПЛОМНАЯ РАБОТА по теме: “Олимпиада по математике
- 3. Цель дипломной работы заключается в изучении методических
- 4. Под внеклассной работой по математике понимаются: необязательные
- 5. Основными целями и задачами предметных конкурсов, олимпиад
- 6. подготовка к конкурсам и олимпиадам
- 7. Основные формы по подготовке к математическим конкурсам,
- 8. Что необходимо школьнику для успешного участия в
- 9. Разрезание и замощение 5 класс Разрезать фигуру
- 10. 7 класс Сколькими способами можно разрезать
- 11. 5 класс Можно ли на доске
- 12. Делимость 5 класс На точно идущих двенадцатичасовых
- 13. Рыцари, лжецы и хитрецы 7 класс На
- 14. 8 класс На острове живут рыцари, которые
- 15. В результате проделанной работы были решены следующие
- 16. Спасибо за внимание!
- 17. Цель дипломной работы заключается в изучении методических
- 18. Под внеклассной работой по математике понимаются: необязательные
- 19. Основными целями и задачами предметных конкурсов, олимпиад
- 20. подготовка к конкурсам и олимпиадам
- 21. Основные формы по подготовке к математическим конкурсам,
- 22. Что необходимо школьнику для успешного участия в
- 23. Разрезание и замощение 5 класс Разрезать фигуру
- 24. 7 класс Сколькими способами можно разрезать
- 25. 5 класс Можно ли на доске
- 26. Делимость 5 класс На точно идущих двенадцатичасовых
- 27. Рыцари, лжецы и хитрецы 7 класс На
- 28. 8 класс На острове живут рыцари, которые
- 29. В результате проделанной работы были решены следующие
- 30. Спасибо за внимание!
ДИПЛОМНАЯ РАБОТА по теме: “Олимпиада по математике в 5 - 8 классах” Выполнила: Скрынник Дарья
Слайд 3Цель дипломной работы заключается в изучении методических подходов к подготовке учащихся
5–8 классов к участию в математических конкурсах, олимпиадах и разработке заданий для олимпиады по математике.
Слайд 4Под внеклассной работой по математике понимаются: необязательные систематические занятия учащихся с
учителем во внеурочное время.
Существуют следующие формы внеклассной работы:
— математический кружок;
— факультативные занятия;
— математические олимпиады, конкурсы, викторины;
— математические игры;
— математические дискуссии;
— неделя математики;
— изготовление математических моделей.
Существуют следующие формы внеклассной работы:
— математический кружок;
— факультативные занятия;
— математические олимпиады, конкурсы, викторины;
— математические игры;
— математические дискуссии;
— неделя математики;
— изготовление математических моделей.
Слайд 5Основными целями и задачами предметных конкурсов, олимпиад являются:
— пропаганда научных знаний
и развитие у обучающихся интереса к научной деятельности;
— создание необходимых условий для выявления одаренных детей;
— организация работы факультативных занятий, кружков;
— активизация (мотивация, привлечение) к деятельности учащихся в научном обществе учащихся.
— создание необходимых условий для выявления одаренных детей;
— организация работы факультативных занятий, кружков;
— активизация (мотивация, привлечение) к деятельности учащихся в научном обществе учащихся.
Слайд 7Основные формы по подготовке к математическим конкурсам, олимпиадам:
Математический кружок;
Факультативные занятия по
математике;
Исследовательская деятельность;
Проект.
Исследовательская деятельность;
Проект.
Слайд 8Что необходимо школьнику для успешного участия в интеллектуальном состязании?
Развитый математический кругозор;
Умение
решать нестандартные задачи, владение необходимым для этого математическим аппаратом;
Практические умения и навыки, знание основных приемов, способов решения математических задач.
Практические умения и навыки, знание основных приемов, способов решения математических задач.
Слайд 9Разрезание и замощение
5 класс
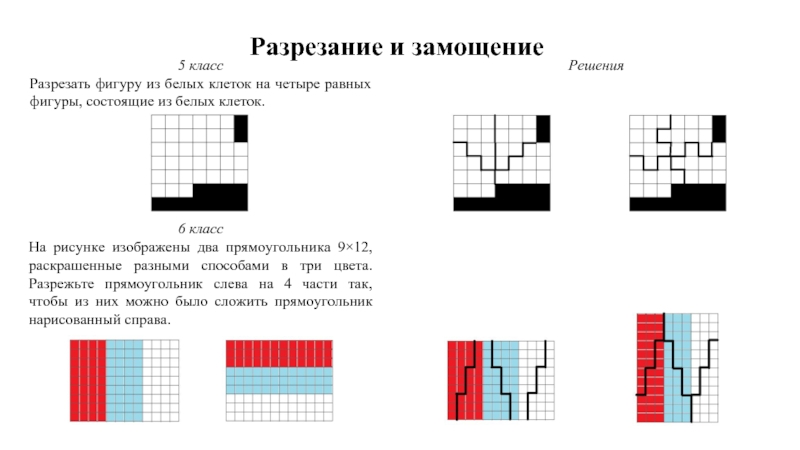
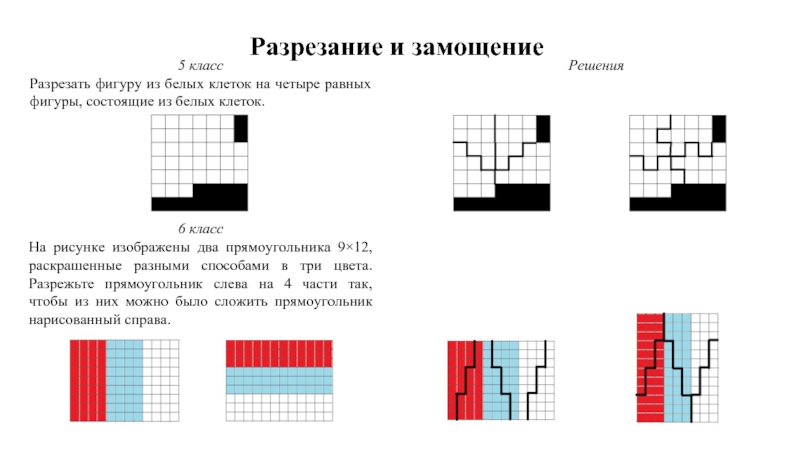
Разрезать фигуру из белых клеток на четыре равных
фигуры, состоящие из белых клеток.
6 класс
На рисунке изображены два прямоугольника 9×12, раскрашенные разными способами в три цвета. Разрежьте прямоугольник слева на 4 части так, чтобы из них можно было сложить прямоугольник нарисованный справа.
Решения
Слайд 107 класс
Сколькими способами можно разрезать фигуру из белых клеток (см. рис.)
на домино размером 2×1?
8 класс
Из доски 8×8 вырезан в углу квадрат 6×6. Двое по очереди ставят на получившуюся доску непересекающиеся уголки из трех клеток (по линиям сетки). Кто не может поставить уголок, тот проиграл. Кто выиграет при правильной игре?
Решения
Слайд 115 класс
Можно ли на доске 7×7 расставить 25 рыцарей и 24
лжеца (по одному в каждой клетке) так, чтобы каждый из них мог сказать: «Рядом со мной стоит ровно один рыцарь»? Люди стоят рядом, если у клеток, в которых они стоят, есть общая сторона. Рыцари всегда говорят правду, а лжецы всегда лгут. Ответ обоснуйте.
7 класс
На шахматной доске 8×8 стоят 10 шахматных фигур (слоны и ладьи), не бьющих друг друга. Какое наименьшее количество слонов может быть среди них? Ладьи бьют только по вертикалям и горизонталям, а слоны только по диагоналям.
Решения
Слайд 12Делимость
5 класс
На точно идущих двенадцатичасовых часах часовая стрелка в данный момент
показывает на отметку «44 минуты». Что показывает минутная стрелка?
Решение
44×12=528=8×60+48.
6 класс
Придумайте 25-значное число без нулевых цифр, делящееся на сумму своих цифр. Обоснуйте, что оно удовлетворяет всем условиям задачи.
Решение
Пусть сумма цифр 36, значит число делится на 9.
Возьмем последние две цифры так, чтобы число делилось на 4, например 44.
Остальные 23 цифры составим из восемнадцати 1 и пяти 2 чтобы в сумме все цифры включая последние давали 36.
7 класс
На столе лежит куча из 1001 камня. Из нее выкидывают камень и кучу делят на две. Затем из какой-либо кучи, содержащей более одного камня, снова выкидывают камень, и снова одну кучу делят на две. И так далее. Можно ли через несколько ходов оставить на столе только кучи, состоящие из трех камней?
Решение
Пусть за k ходов мы разбили кучу на (k+1) кучку по 3 камня. Тогда отброшено k камней и всего камней k+3(k+1)=4k+3=1001. Но 998≠4k. Противоречие.
8 класс
Докажите, что для любого натурального числа n можно выбрать такое натуральное число а, чтобы число а(n +1) – (n2 + n + 1) нацело делилось на n3.
Решение
a=n2+1. Тогда (n2+1)(n +1) – (n2 + n + 1) = n3.
Слайд 13Рыцари, лжецы и хитрецы
7 класс
На острове живут рыцари, которые всегда говорят
правду, лжецы, которые всегда лгут, и хитрецы, которые могут говорить что угодно. Из трёх жителей острова А, В и С один является правдолюбцем, другой — лжецом, а третий — хитрецом. Они произнесли следующие утверждения — А: «С хитрец»; В: «Это правда»; С: «В не рыцарь». Кем в действительности является С?
Решение
Рыцарь
Хитрец
Лжец
А
В
С
А
С
В
А
А
С
В
В
С
«С хитрец»
«Это правда»
«В не рыцарь»
«С хитрец»
«В не рыцарь»
«Это правда»
«Это правда»
«Это правда»
«С хитрец»
«С хитрец»
«В не рыцарь»
«В не рыцарь»
Слайд 148 класс
На острове живут рыцари, которые всегда говорят правду, лжецы, которые
всегда лгут, и хитрецы, которые могут говорить что угодно. Из трёх жителей острова: К, М и Р один является правдолюбцем, другой — лжецом, а третий — хитрецом. Они произнесли следующие утверждения — К: «Р не хитрец». М: «Это ложь». Р: «К рыцарь». Кем в действительности являются К, М и Р?
Решение
Рыцарь
Хитрец
Лжец
К
Р
М
К
М
Р
К
К
М
Р
Р
М
«Р не хитрец»
«К рыцарь»
«Это ложь»
«Р не хитрец»
«Это ложь»
«К рыцарь»
«К рыцарь»
«К рыцарь»
«Р не хитрец»
«Р не хитрец»
«Это ложь»
«Это ложь»
Слайд 15В результате проделанной работы были решены следующие задачи:
1. Проанализирована научная и
учебно‒методическая литература по математике;
2. Разработанные задания для олимпиады по математике для 5‒8 классов содержат материал, занимательного характера.
Вывод: Олимпиады способствуют повышению интереса учащихся к предмету и воспитанию высокой культуры математического мышления.
2. Разработанные задания для олимпиады по математике для 5‒8 классов содержат материал, занимательного характера.
Вывод: Олимпиады способствуют повышению интереса учащихся к предмету и воспитанию высокой культуры математического мышления.
Слайд 17Цель дипломной работы заключается в изучении методических подходов к подготовке учащихся
5–8 классов к участию в математических конкурсах, олимпиадах и разработке заданий для олимпиады по математике.
Слайд 18Под внеклассной работой по математике понимаются: необязательные систематические занятия учащихся с
учителем во внеурочное время.
Существуют следующие формы внеклассной работы:
— математический кружок;
— факультативные занятия;
— математические олимпиады, конкурсы, викторины;
— математические игры;
— математические дискуссии;
— неделя математики;
— изготовление математических моделей.
Существуют следующие формы внеклассной работы:
— математический кружок;
— факультативные занятия;
— математические олимпиады, конкурсы, викторины;
— математические игры;
— математические дискуссии;
— неделя математики;
— изготовление математических моделей.
Слайд 19Основными целями и задачами предметных конкурсов, олимпиад являются:
— пропаганда научных знаний
и развитие у обучающихся интереса к научной деятельности;
— создание необходимых условий для выявления одаренных детей;
— организация работы факультативных занятий, кружков;
— активизация (мотивация, привлечение) к деятельности учащихся в научном обществе учащихся.
— создание необходимых условий для выявления одаренных детей;
— организация работы факультативных занятий, кружков;
— активизация (мотивация, привлечение) к деятельности учащихся в научном обществе учащихся.
Слайд 21Основные формы по подготовке к математическим конкурсам, олимпиадам:
Математический кружок;
Факультативные занятия по
математике;
Исследовательская деятельность;
Проект.
Исследовательская деятельность;
Проект.
Слайд 22Что необходимо школьнику для успешного участия в интеллектуальном состязании?
Развитый математический кругозор;
Умение
решать нестандартные задачи, владение необходимым для этого математическим аппаратом;
Практические умения и навыки, знание основных приемов, способов решения математических задач.
Практические умения и навыки, знание основных приемов, способов решения математических задач.
Слайд 23Разрезание и замощение
5 класс
Разрезать фигуру из белых клеток на четыре равных
фигуры, состоящие из белых клеток.
6 класс
На рисунке изображены два прямоугольника 9×12, раскрашенные разными способами в три цвета. Разрежьте прямоугольник слева на 4 части так, чтобы из них можно было сложить прямоугольник нарисованный справа.
Решения
Слайд 247 класс
Сколькими способами можно разрезать фигуру из белых клеток (см. рис.)
на домино размером 2×1?
8 класс
Из доски 8×8 вырезан в углу квадрат 6×6. Двое по очереди ставят на получившуюся доску непересекающиеся уголки из трех клеток (по линиям сетки). Кто не может поставить уголок, тот проиграл. Кто выиграет при правильной игре?
Решения
Слайд 255 класс
Можно ли на доске 7×7 расставить 25 рыцарей и 24
лжеца (по одному в каждой клетке) так, чтобы каждый из них мог сказать: «Рядом со мной стоит ровно один рыцарь»? Люди стоят рядом, если у клеток, в которых они стоят, есть общая сторона. Рыцари всегда говорят правду, а лжецы всегда лгут. Ответ обоснуйте.
7 класс
На шахматной доске 8×8 стоят 10 шахматных фигур (слоны и ладьи), не бьющих друг друга. Какое наименьшее количество слонов может быть среди них? Ладьи бьют только по вертикалям и горизонталям, а слоны только по диагоналям.
Решения
Слайд 26Делимость
5 класс
На точно идущих двенадцатичасовых часах часовая стрелка в данный момент
показывает на отметку «44 минуты». Что показывает минутная стрелка?
Решение
44×12=528=8×60+48.
6 класс
Придумайте 25-значное число без нулевых цифр, делящееся на сумму своих цифр. Обоснуйте, что оно удовлетворяет всем условиям задачи.
Решение
Пусть сумма цифр 36, значит число делится на 9.
Возьмем последние две цифры так, чтобы число делилось на 4, например 44.
Остальные 23 цифры составим из восемнадцати 1 и пяти 2 чтобы в сумме все цифры включая последние давали 36.
7 класс
На столе лежит куча из 1001 камня. Из нее выкидывают камень и кучу делят на две. Затем из какой-либо кучи, содержащей более одного камня, снова выкидывают камень, и снова одну кучу делят на две. И так далее. Можно ли через несколько ходов оставить на столе только кучи, состоящие из трех камней?
Решение
Пусть за k ходов мы разбили кучу на (k+1) кучку по 3 камня. Тогда отброшено k камней и всего камней k+3(k+1)=4k+3=1001. Но 998≠4k. Противоречие.
8 класс
Докажите, что для любого натурального числа n можно выбрать такое натуральное число а, чтобы число а(n +1) – (n2 + n + 1) нацело делилось на n3.
Решение
a=n2+1. Тогда (n2+1)(n +1) – (n2 + n + 1) = n3.
Слайд 27Рыцари, лжецы и хитрецы
7 класс
На острове живут рыцари, которые всегда говорят
правду, лжецы, которые всегда лгут, и хитрецы, которые могут говорить что угодно. Из трёх жителей острова А, В и С один является правдолюбцем, другой — лжецом, а третий — хитрецом. Они произнесли следующие утверждения — А: «С хитрец»; В: «Это правда»; С: «В не рыцарь». Кем в действительности является С?
Решение
Рыцарь
Хитрец
Лжец
А
В
С
А
С
В
А
А
С
В
В
С
«С хитрец»
«Это правда»
«В не рыцарь»
«С хитрец»
«В не рыцарь»
«Это правда»
«Это правда»
«Это правда»
«С хитрец»
«С хитрец»
«В не рыцарь»
«В не рыцарь»
Слайд 288 класс
На острове живут рыцари, которые всегда говорят правду, лжецы, которые
всегда лгут, и хитрецы, которые могут говорить что угодно. Из трёх жителей острова: К, М и Р один является правдолюбцем, другой — лжецом, а третий — хитрецом. Они произнесли следующие утверждения — К: «Р не хитрец». М: «Это ложь». Р: «К рыцарь». Кем в действительности являются К, М и Р?
Решение
Рыцарь
Хитрец
Лжец
К
Р
М
К
М
Р
К
К
М
Р
Р
М
«Р не хитрец»
«К рыцарь»
«Это ложь»
«Р не хитрец»
«Это ложь»
«К рыцарь»
«К рыцарь»
«К рыцарь»
«Р не хитрец»
«Р не хитрец»
«Это ложь»
«Это ложь»
Слайд 29В результате проделанной работы были решены следующие задачи:
1. Проанализирована научная и
учебно‒методическая литература по математике;
2. Разработанные задания для олимпиады по математике для 5‒8 классов содержат материал, занимательного характера.
Вывод: Олимпиады способствуют повышению интереса учащихся к предмету и воспитанию высокой культуры математического мышления.
2. Разработанные задания для олимпиады по математике для 5‒8 классов содержат материал, занимательного характера.
Вывод: Олимпиады способствуют повышению интереса учащихся к предмету и воспитанию высокой культуры математического мышления.
