- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дарынды оқушыларды пәндік олимпиадаға дайындаудың тиімді жолдары презентация
Содержание
- 1. Дарынды оқушыларды пәндік олимпиадаға дайындаудың тиімді жолдары
- 2. Мақсаты: оқушылардың математика бойынша білім мен білік деңгейін,
- 3. Міндеттері: оқушылардың оқу- танымдық және оқу-зерттеу интеллектілерін
- 4. Бізге керегі – шын дарындар. Нарық қол-аяғымызды
- 5. Дарынды балаларды айрықша оқшауландыратын ерекшеліктер: ақыл-ой
- 6. ДАРЫНДЫ БАЛАЛАРМЕН ЖҰМЫС ІСТЕУДЕ НЕНІ ЕСКЕРУ КЕРЕК?
- 7. ДАРЫНДЫ БАЛАНЫҢ СИПАТТАМАСЫ: Білімділік өрісі Интеллектуалдық сферасы.
- 8. ДАРЫНДЫЛЫҚ ҮШ ПАРАМЕТРМЕН АНЫҚТАЛАДЫ: Танымдылық жеке дамуы Психологиялық дамуы Физикалық дамуы
- 9. ДАРЫНДЫЛЫҚТЫ АНЫҚТАҒАНДА ТӨМЕНДЕГІ ФАКТОРЛАРДЫ ЕСКЕРУ
- 10. Дарынды бала – бұл белгілі бір салада
- 11. Әлімбетов Н. Бейсеков Ж. Мирсоатов
- 12. Пуассон теңдеуі — оператор
- 13. Бұл принципті қолданудың бірнеше түрі бар,
- 14. 1) Кук қиындығы Бір де бір есеп
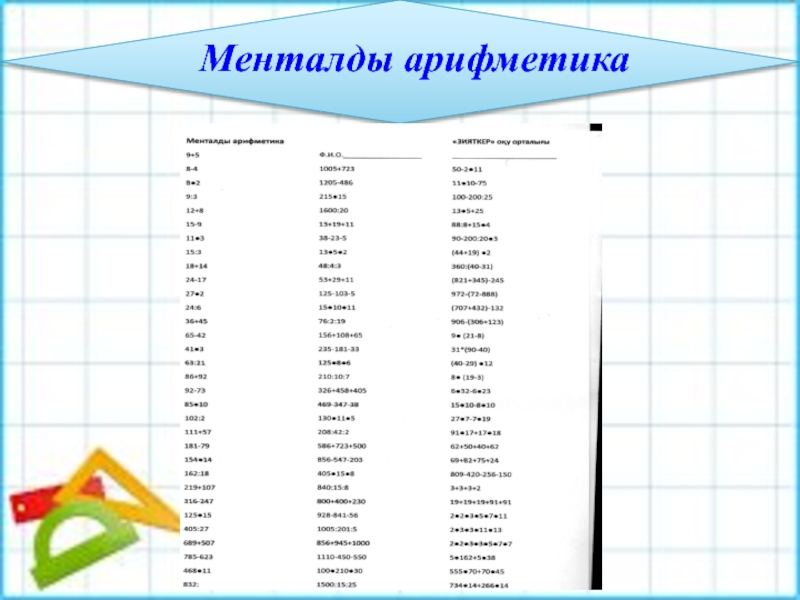
- 15. Менталды арифметика
- 16. Кубик – рубик ойыны
- 17. Шахмат ойыны
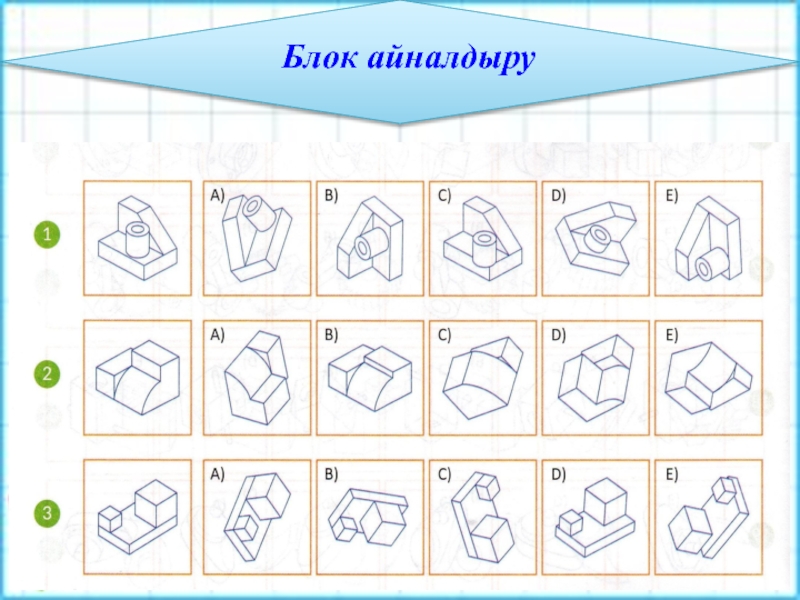
- 18. Блок айналдыру
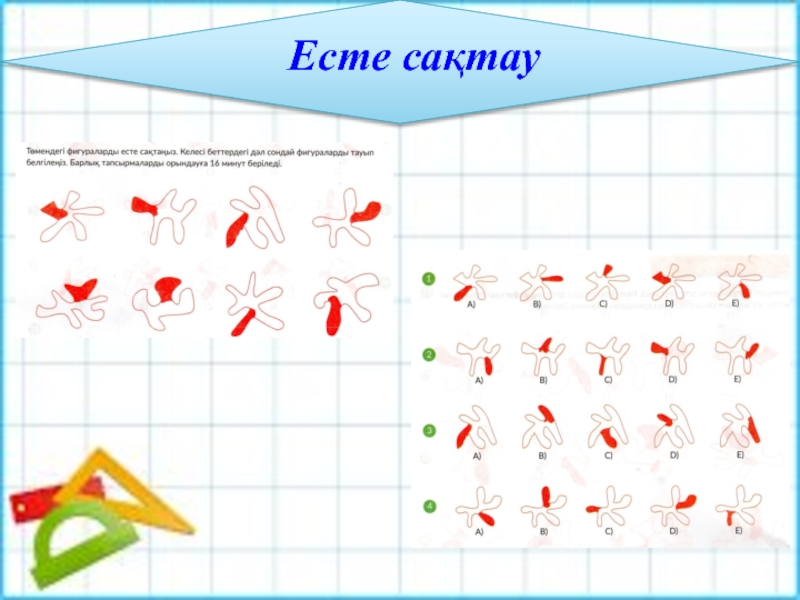
- 19. Есте сақтау
- 20. Нұрланқызы Нұрбала «Ақ бота - 2013 »
- 21. Кендебай Дәулет Ресей білімді қолдау қорының ұйымдастырумен
- 22. Ресей білімді қолдау қорының ұйымдастырумен өткен «Читающий
- 23. Республикалық “АҚБОТА-2017” интеллектуалдық марафонының қорытындысы І орын
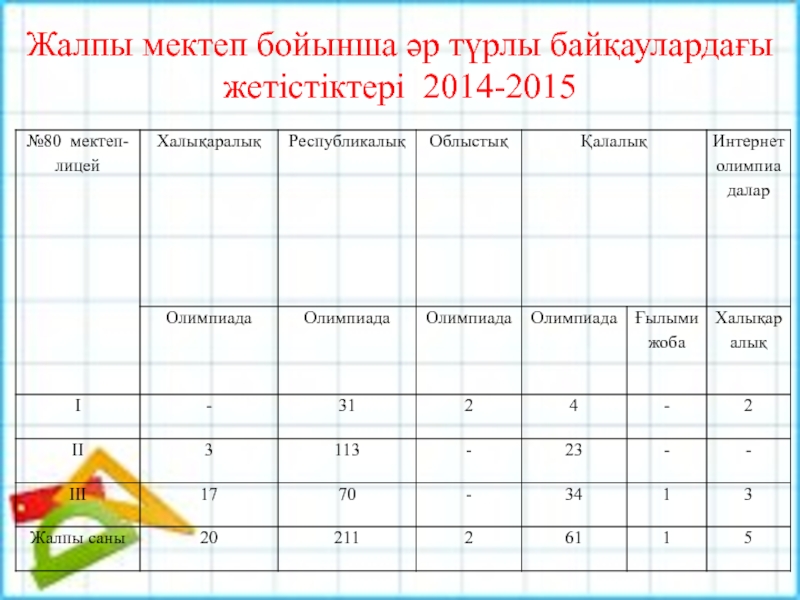
- 24. Жалпы мектеп бойынша әр түрлы байқаулардағы жетістіктері 2014-2015
- 25. Жалпы мектеп бойынша әр түрлы байқаулардағы жетістіктері 2015-2016
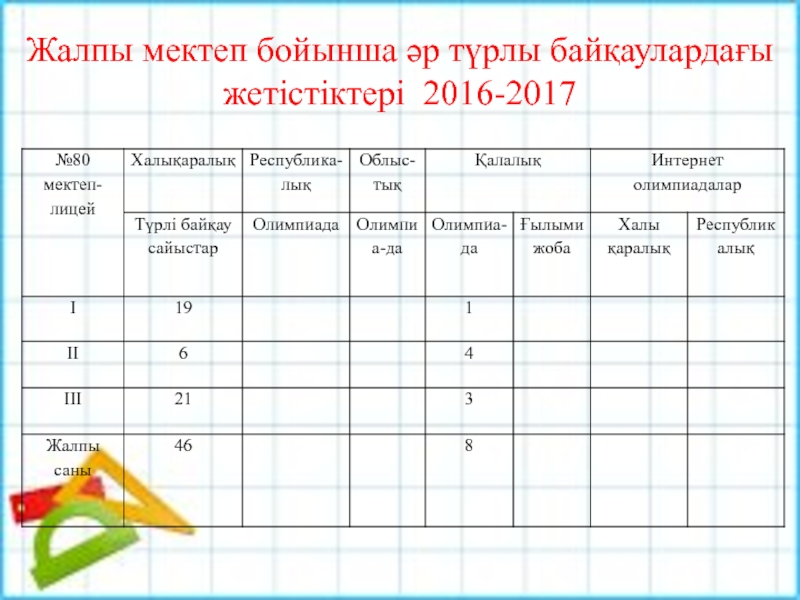
- 26. Жалпы мектеп бойынша әр түрлы байқаулардағы жетістіктері 2016-2017
- 27. 2017 жылғы 26 мамыр мен 03 маусым
- 28. Қорыта келген кезде, жалпы дарынды
Слайд 2Мақсаты: оқушылардың математика бойынша білім мен білік деңгейін, қалыптасқан таным түсінік, инттеллектуалдық,
аналитикалық ойлау шеберліктері мен мәселені қорытып, жүйелі түрде саралай білудегі жүйріктік пен алғырлық, тапқырлық, т.б қасиеттері тұрғысынан өз замандастары арасында бәсекеге қабілеттілік дағдыларын
шыңдау. Жастардың бойындағы ынталылық, ойлылық, дарындылық, талаптылық, білімділік сынды озық қасиеттерді насихаттап, көшпілікке таныту. Сондай-ақ олимпиадалық байқау нәтижелері бойынша топ жарған жеңімпаз ретінде таныла білген талапты да, талантты жастардың алықаралық деңгейдегі олимпиадалар мен түрлі конкурстарға, жарыстарға атсалысу мүмкіндіктерін арттыру.
Слайд 3Міндеттері:
оқушылардың оқу- танымдық және оқу-зерттеу интеллектілерін
ынталандыру;
оқушылардың жеке кәсіби әлеуетін, шығармашылық
шыңдау, олардың өз мүмкіндіктерін барынша жүзеге асыра білу;
оқушылардың толыққанды жеке тұлға ретіндегі азаматтық
ұстанымын орнықтыру;
білімді де білікті, жаңашыл таным көзқарасты, дарынды
оқушыларды іріктеу және қолдау;
оқушылардың білім беру жүйесін жетілдіру тұрғысындағы
кәсіби-шығармашылық, белсенділік қатынасын қалыптастыру.
Слайд 4Бізге керегі – шын дарындар. Нарық қол-аяғымызды қалай қыспасын, мемлекет өзінің
Н.Ә.Назарбаев
Слайд 5Дарынды балаларды айрықша
оқшауландыратын ерекшеліктер:
ақыл-ой еңбегіне бейімділік,
жоғары зерттеушілік қабілеті мен
танымдық
білімі,
жаңа хабарды ұдайы қабылдауға
ұмтылыс, яғни танымдық қажеттілік.
Бақылаулар көрсеткендей, жоғары танымдық
қажеттілік баланың өз талпынысымен болады.
Дарынды балалар қиын тапсырмаларды
құштарлықпен оңай орындайды.
Дайын жауаптарды ұнатпайды.
Слайд 6ДАРЫНДЫ БАЛАЛАРМЕН ЖҰМЫС ІСТЕУДЕ
НЕНІ ЕСКЕРУ КЕРЕК?
Балаларның пәнге қызығушылығын,
білуге құштарлығын нақты
Балаға тапсырманы деңгейлеп беріп,
зейінін тұрақтандыру қажет.
Баланың мінезін – құлқын ерекшелігін
білу.(Нені ұнатады, нені ұнатпайды,қай
кезде білімді жақсы меңгереді, қай кезде шаршайды? т.б)
Берілген тапсырманы бірлесе талдау.
Баланың бір қалыпты, жүйелі жұмыс
жасауына көңіл бөлу.
Бала қызығушылығына қолдау көрсету,
орынды кеңес бере білудің маңызы зор.
Слайд 7ДАРЫНДЫ БАЛАНЫҢ СИПАТТАМАСЫ:
Білімділік өрісі
Интеллектуалдық сферасы.
Ойлау қабілеті ерекшесі тұрақты,
қызығуы мол, кейде
айналысса тоқтай алмайды,
өз ойын ерте жеткізеді.
Слайд 9ДАРЫНДЫЛЫҚТЫ АНЫҚТАҒАНДА
ТӨМЕНДЕГІ ФАКТОРЛАРДЫ
ЕСКЕРУ КЕРЕК
Жас ерекшелігі
Тұлғалық ерекшелігі
Экспериментатордың тұлғалық ерекшелігін
Слайд 10Дарынды бала – бұл белгілі бір салада
жетістіктері айқын көрінетін немесе
сондай жетістіктер әлеуеті мол бала
Н.С.Лейтис
Слайд 11Әлімбетов Н.
Бейсеков Ж.
Мирсоатов
Ж.Б. Қалтаева
Омаров Ә.К.
Бейсеков.Ж
Тәңірбергенов Ә
Ж.Бейсеков
Л.Э.Генденштейн
А.П.Ершова
А.С.Ершова
Олимпиадаға дайындық материалдары
Слайд 12Пуассон теңдеуі
— оператор Лапласа
— вещественная или комплексная функция
Үш
декарттық санақ жүйесінде лаплас операторы түріне озгереді.
Яғни,
— электростатический потенциал, —зарядтың көлемдік
тығыздығы.
Пуассон теңдеуі және оның жалпы шешімі
Слайд 13 Бұл принципті қолданудың бірнеше түрі бар, кең таралғаны мынадай:
«егер
онда кем дегенде бір үйшікте екі қоян табылады. Дирихле принципінің
кейбір түрлері: 1) «Қанша алу керек?»...; 2) «...кем дегенде екеу табылатынын
дәлелдеңіз»; 3) «Дирихленің жалпылама принципі».
Мысал қарастырайық: кез келген 13 оқушының туған айлары бірдей кем
дегенде екі оқушы табылатынын көрсетейік.
Шешуі: Бір жылда барлығы 12 ай болғандықтан, 13 оқушының кем
дегенде екеуі бір айда туады.
Дирихле принципі
(ағылшын тілі мен кейбір басқа да тілдерде «кептерлер мен жәшіктер принципі»)
Слайд 141) Кук қиындығы
Бір де бір есеп шешімінің дұрыстығын тексеру, сол шешімді
Бұл логикалық есеп криптография (ақпаратты шифрлау) негіздерін «адам танымастай» өзгертер еді.
2) Риман гипотезасы
2, 3, 5, 7, т.т сияқты өзіне ғана бөлінетін жай сандар бар. Қанша жай сан бар екені белгісіз. Шешімі бар
екенін және олардың таралу заңдылықтарын анықтауға болатынын Риман болжаған. Кімде кім
тапса – криптографияға үлкен қызмет болар еді.
3) Берч және Свиннертон-Дайер гипотезасы
Қиындық – дәрежелі үш белгісізі бар теңдеуді( x2 + y2 = z2 типтес) шешумен байланысты.
Күрделілігі әр түрлі теңдеулерге жарайтын тәсіл табу керек. Евклид x2 + y2 = z2 теңдеуінің
шешімін толығымен түсіндіріп кеткен. Бірақ, күрделі теңдеулерді шешуге өте қиын.
4) Ходж гипотезасы
Күрделі объекттердің формасын зерттеу амалдарын математиктер ХХ ғасырда тапқан.
Гипотезаның негізгі идеясы объекттің орнына қарапайым «кірпіштерді» қолдану. Ол «кірпіштер»
өзара жабыстырылған және объекттің көшірмесіндей. Объект құрастыруға болатынын және бұның
әр уақыттамүмкін екенін дәлелдеу керек.
5) Навье-Стокс теңдеуі
Ұшақта отырып есіңізге түсіріңіз. Теңдеу ұшақты ауада «қалқытатын» ауа ағындарын сипаттайды.
Қазіргі күні жорамалдап шығарады, жорамал формулалармен. Дәл теңдеуді анықтап, әрдайым
дұрыс және үш-өлшемді кеңістікте (трехмерое пространство) шешімі бар теңдеулер барын дәлелдеу керек.
6) Янг-Миллс теңдеуі
Физика әлемінде гипотеза бар: егер элементар бөлшектерде масса болса, онда оның төменгі шегі де болады.
Қандай екені – белгісіз. Бұл ең қиын есептердің бірі. Шешімін табу үшін, табиғаттағы барлық әрекеттесу
күштерін байланыстыратын «барлық теория» теңдеуін ойлап табу керек. Тапқан адам, сөзсіз Нобель
сыйлығын алар еді.
7) Д’Аламбер-Эйлер парадоксы
Бұл парадокс – гидродинамика қағидасы, кез-келген шектеулі формалы дененің шексіз сығылмайтын,
тұтқырлықсыз, әрі құйынтуғызбайтын және жылдамдық үзілу жазықтықтарынсыз сұйықтықтың
ішіндегі бірқалыпты және сызықтық қозғалысы кезінде сұйықтықтың дене қозғалысына қорытынды
үйкеліс күші нөлге тең (1744-жылы Ж. Д’Аламбер, 1745 жылы Л. Эйлер айтқан). Адиабатты қозғалатын
идеал газ үшін дәлелденген. Физикалық үйкеліс күшінің жоқтығы жоғарыда айтылған жағдайларда
сұйықтық не газ ағындары қозғалыстағы дененің арт жағында тұйықталуымен түсіндіріледі, жалпы
сұйқтық арт жаққа әсер ете отырып, алдыңғы жаққа түсірілетін күшті теңестіреді.
Слайд 20Нұрланқызы Нұрбала
«Ақ бота - 2013 » ІІ орын
«Самұрық» І
23rd Mathematics and Informatics Tournament
CHERNORIZEC HRABAR ІІ орын
«Самұрық» ІІ орын
«Самұрық» ІІ орын
Облыстық пәнаралық олимпиада І орын (7 сынып)
Қалалық пәнаралық олимпиада І орын (5 сынып)
Қалалық пәнаралық олимпиада І орын (8 сынып)
«Интелектуал -2050»
«Кенгуру» І орын
Слайд 21Кендебай Дәулет
Ресей білімді қолдау қорының ұйымдастырумен өткен «Читающий человек –
Слайд 22Ресей білімді қолдау қорының ұйымдастырумен өткен «Читающий человек – будущий ученый
Тагаева Аселайым
Слайд 23Республикалық “АҚБОТА-2017” интеллектуалдық марафонының қорытындысы
І орын – 51 оқушы
ІІ орын –
ІІІ орын – 65 оқушы
Халықаралық математикалық олимпиада жеңімпаздары
(Алматы қаласы, Талғар ауданы)
ІІ орын – 3 оқушы
ІІІ орын – 5 оқушы
Халықаралық қашықтықтан өткен конкурстар
“Осень-2016” ағылшын тілі пәндік олимпиадасы
І орын -19 оқушы
ІІ орын 10 оқушы
ІІІ орын – 16 оқушы
Слайд 272017 жылғы 26 мамыр мен 03 маусым аралығында – Францияда
2017
2017 жылғы 04 шілде мен 11 шілде аралығында Болгарияда
ЖАЗҒЫ ОЛИМПИАДАЛАР
Слайд 28
Қорыта келген кезде, жалпы дарынды баланы анықтау
және қолдау алдындағы оқытушы
Шеберлігін қажет етеді. Бүгінгі таңдағы зерделі де
зейінді дара тұлғаның бойындағы жеке қасиеттерді
дамыту үшін бағдарламалар мен әр түрлі іс-шаралар
жетерлік. Дегенмен, бұған біз, ұстаздар қауымы, әлі
де болса өз үлесімізді қосуымыз қажет деп санаймын.