- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Чотирикутники навколо нас презентация
Содержание
- 1. Чотирикутники навколо нас
- 2. Вивчили та повторили: Під час роботи над
- 3. Встановили відповіді на запитання: Як геометрія допомагає
- 4. Родичі Жила на світі важлива фігура.
- 5. Кого зустрічала вона на своєму шляху,
- 6. А звати цю фігуру – Квадрат!!!
- 7. Ходив Квадрат по світу. І почало обтяжувати
- 8. Одного разу зустрічає він на шляху таку
- 9. А звати цю фігуру – Прямокутник!!!
- 10. Як тебе звуть? Довго я шукав
- 11. А звати цю фігуру – Трапеція!!!
- 12. Висновок: Чотирикутником називають частину площини обмежену чотирма
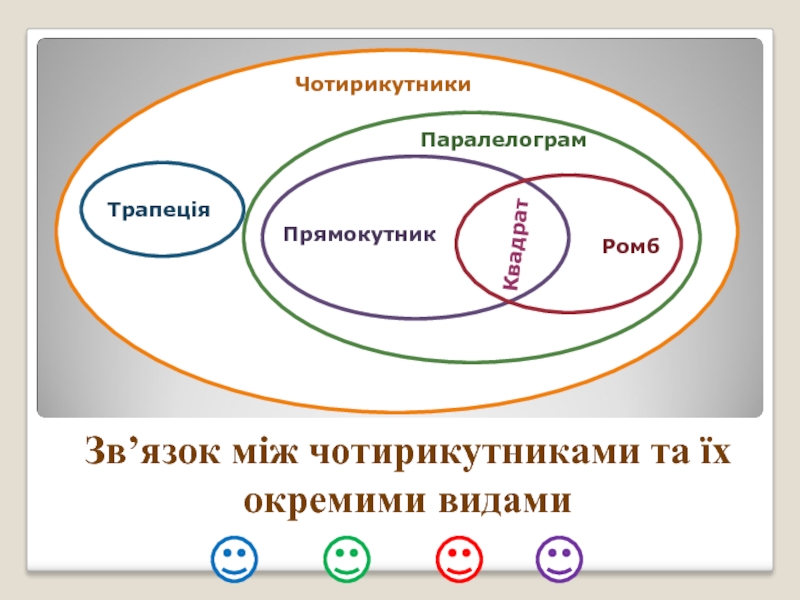
- 13. Зв’язок між чотирикутниками та їх окремими видами
- 14. Пояснення. Тепер
- 15. Напрямки пошуку відповіді на друге
- 16. У мистецтві
- 17. У будівництві
- 19. Дякуємо за увагу!
Слайд 2 Вивчили та повторили:
Під час роботи над проектом ми вивчили теоретичний матеріал,
Які властивості має квадрат? Який чотирикутник називають трапецією?
Проаналізували:
Використання теоретичного матеріалу під час розв'язування завдань;
Використання чотирикутників у житті та навели приклади.
Слайд 3Встановили відповіді на запитання:
Як геометрія допомагає у житті?
Чи може бути так,
Слайд 4Родичі
Жила на світі важлива фігура.
Важливість її визнавалася всіма людьми,
оскільки
речей форма її служила зразком.
А мала вона такий вигляд:
Слайд 5Кого зустрічала вона на своєму шляху,
всім хвалилася:
Подивіться, який у мене
Як же звуть тебе, брат?
Слайд 6
А звати цю фігуру – Квадрат!!!
Примітка.
У квадрата:
Всі сторони рівні.
Сторони попарно паралельні,
Всі кути рівні і градусна міра кожного з них дорівнює 90 .
Діагоналі рівні, перетинаються під прямим кутом і є бісектрисами його кутів.
Діагоналі перетинаються і точкою перетину діляться пополам.
0
0
Слайд 7Ходив Квадрат по світу. І почало обтяжувати його самота: ні поговорити
А вже яка веселість одному! Весело буває тільки разом з друзями. І вирішив Квадрат пошукати родичів.
Якщо зустріну родича, то я його відразу впізнаю, адже він на мене повинен бути чимось схожий.
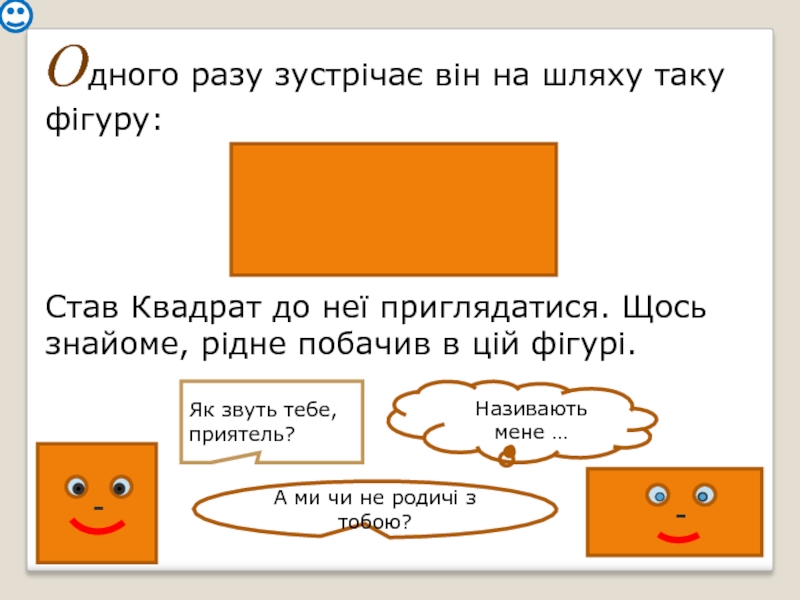
Слайд 8Одного разу зустрічає він на шляху таку фігуру:
Став Квадрат до неї
Як звуть тебе, приятель?
Називають мене …
А ми чи не родичі з тобою?
Слайд 9
А звати цю фігуру – Прямокутник!!! Прямокутник із квадратом родичі, бо
Примітка.
У прямокутника і квадрата:
Сторони попарно паралельні, тобто лежать на паралельних прямих.
Протилежні сторони рівні.
Всі кути рівні і градусна міра кожного з них дорівнює 90 .
Діагоналі рівні.
Діагоналі перетинаються і точкою перетину діляться пополам.
0
0
Слайд 10Як тебе звуть?
Довго я шукав представників нашого роду. І я вас
А як ти доведеш, що ми родичі?
Зраділи фігури тому, що знайшли один одного. Стали тепер вони удвох жити, разом працювати, разом веселитися, разом і по білому світу мандрувати.
Відпочивають вони одного разу на узліссі і бачать: виходить із-за чагарників якась нова фігура і прямує прямо до них. А вигляд вона мала такий:
Слайд 11
А звати цю фігуру – Трапеція!!! Трапеція із Прямокутником і квадратом
Примітка.
У прямокутника, квадрата і трапеції:
Чотири сторони.
Дві сторони паралельні.
Так зустрілися і почали жити разом три споріднені фігури з давнього роду – Чотирикутників.
Слайд 12Висновок:
Чотирикутником називають частину площини обмежену чотирма відрізками.
Паралелограмом називають чотирикутник, у якого
Прямокутником називають паралелограм, у якого всі кути прямі.
Ромбом називають паралелограм, у якого всі сторони рівні.
Квадратом називають прямокутник, у якого всі сторони рівні.
Трапецією називають чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні.
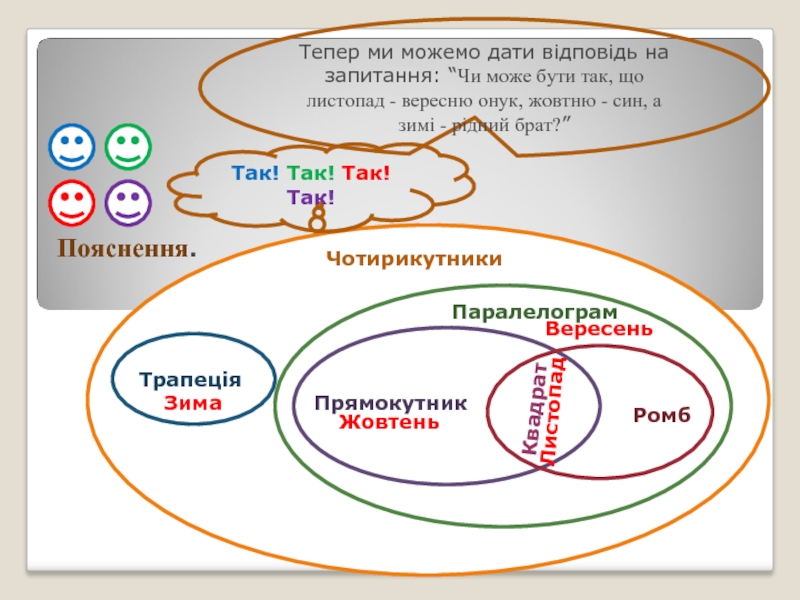
Слайд 14Пояснення.
Тепер ми можемо дати відповідь на запитання: “Чи може бути так,
Листопад
Вересень
Жовтень
Зима
Так! Так! Так! Так!
Слайд 15
Напрямки пошуку відповіді на друге питання: “Як геометрія допомагає у житті?”
У мистецтві
У будівництві
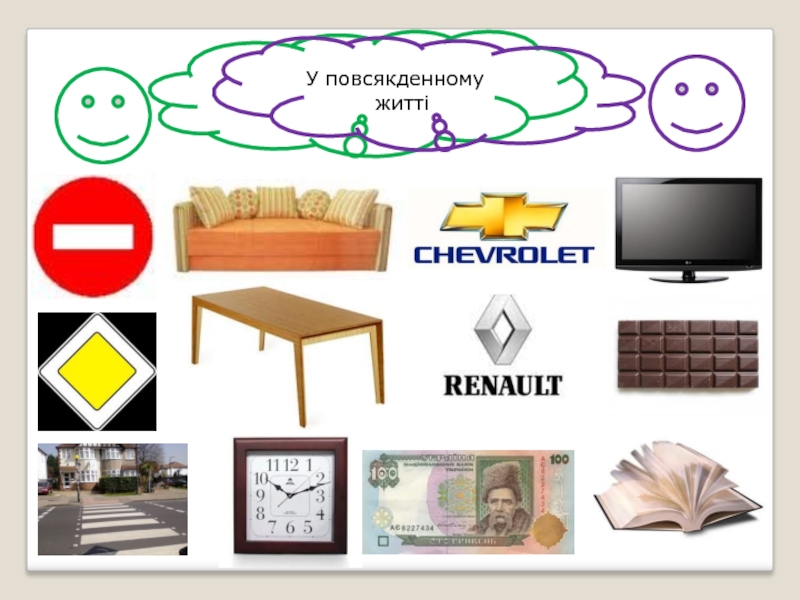
У повсякденному
житті
Слайд 19
Дякуємо за увагу!
Висновок:
Зображення чотирикутників ми можемо спостерігати скрізь, у дома, на
Подивись навкруги і також помітиш цей чарівний світ ЧОТИРИКУТНИКІВ.
Використані ресурси:
101 узор. Доступ: http://www.1001uzor.com/
Живопись. Доступ: http://infa.ws/jivopis/02/46.php
Ювелірні вироби. Доступ: http://www.alljewelrydesigners.com
Гюбер Робер. Доступ: http://magicpowers.narod.ru/hubert_robert.html