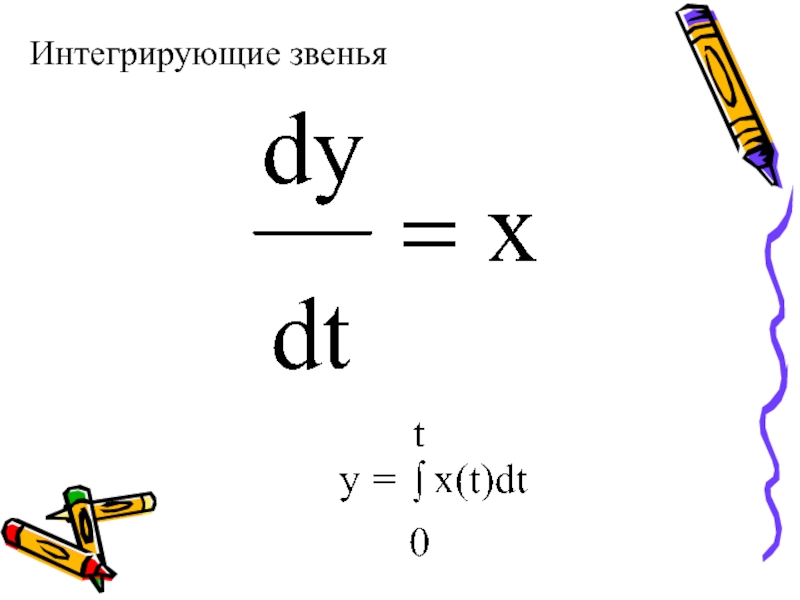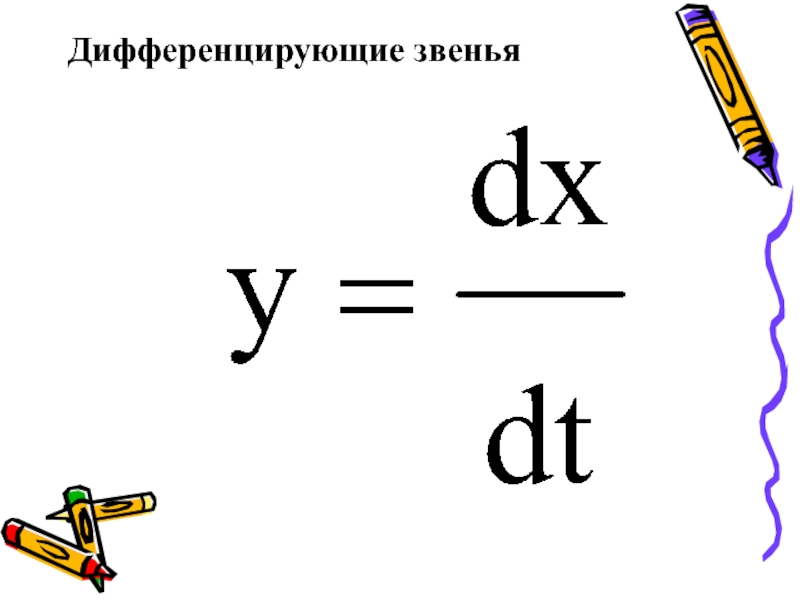- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории управления. Типовые динамические звенья и их характеристики презентация
Содержание
- 1. Основы теории управления. Типовые динамические звенья и их характеристики
- 2. Безынерционное (идеальное усилительное) звено Это
- 3. Апериодическое (инерционное) звено первого порядка (Tp+1)y(t)
- 4. Апериодическое (инерционное) звено второго порядка
- 5. Колебательное звено При Т1≤ 2Т2 корни
- 6. Консервативное звено частный случай колебательного при
- 7. Интегрирующие звенья
- 8. Идеальное интегрирующее звено py(t) = x(t)
- 9. Дифференцирующие звенья
- 10. Идеальное дифференцирующее звено y(t) = px(t),
- 11. Форсирующее (дифференцирующее) звено первого порядка
- 12. Форсирующее (дифференцирующее) звено второго порядка
- 13. Комбинации типовых звеньев Дифференцирующее звено с
- 14. Изодромное звено форсирующее звено первого порядка
- 15. Интегро-дифференцирующее звено апериодическое звено первого порядка
- 16. Неминимально-фазовые звенья звенья, которые, в отличие от
- 17. Звено с положительным полюсом Амплитудно-фазовая частотная
- 18. Звено с положительным нулем W(s) =
Слайд 2Безынерционное
(идеальное усилительное) звено
Это звено не только в статике, но
y(t) = kx(t)
Переходная и импульсная функции:
W(s) = k
Амплитудно-фазовая частотная характеристика
W(jω) = k, A(ω) = k, ψ(ω) = 0
Переходная и импульсная функции
h(t) = k1(t), w(t) = kδ(t)
жесткая механическая передача
часовой редуктор
электронный усилитель сигналов на низких частотах
и др
Слайд 3Апериодическое (инерционное) звено первого порядка
(Tp+1)y(t) = x(t)
Уравнение
T - постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса
Амплитудно-фазовая частотная характеристика
ψ(ω) = - arctgTω
Переходная и импульсная функции
апериодическое звено первого порядка является фильтром низких частот.
RC цепочка, нагревательный элемент
Слайд 4Апериодическое (инерционное) звено второго порядка
При 2Т2≤ Т1 корни вещественные,
(
новые постоянные времени
Передаточная функция звена
двойная RC цепочка, электродвигатель постоянного тока
Слайд 5Колебательное звено
При Т1≤ 2Т2 корни комплексные,
(T2p2+2ξTp+1) y(t) = x(t)
Т - постоянная времени, определяющая угловую частоту свободных колебаний λ=1/Т
ξ - параметр затухания, лежащий в пределах 0<ξ<1
передаточная функция
Амплитудно-фазовая частотная характеристика
Временные характеристики представляют собой затухающие периодические процессы
электрический колебательный контур, электродвигатель постоянного тока, маятник
Слайд 6Консервативное звено
частный случай колебательного при ξ=0
представляет собой идеализированный случай,
Амплитудно-фазовая характеристика совпадает с вещественной осью.
При 0<ω<1/T характеристика совпадает с положительной полуосью,
При ω>1/T - с отрицательной полуосью.
Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T
Слайд 8Идеальное интегрирующее звено
py(t) = x(t)
Амплитудно-фазовая частотная характеристика
Переходная и
h(t) = t, w(t) = 1(t)
операционный усилитель в режиме интегрирования,
гидравлический двигатель,
емкость
Слайд 10Идеальное дифференцирующее звено
y(t) = px(t), W(s) = s
Амплитудно-фазовая
W(jω) = jω, A(ω) = ω, ψ(ω) = +90
Переходная и импульсная функции
операционный усилитель в режиме дифференцирования
Слайд 11Форсирующее (дифференцирующее)
звено первого порядка
y(t) = (τp+1) x(t) ,
τ - постоянная времени дифференцирования
Амплитудно-фазовая частотная характеристика
ψ(ω) = arctg ωτ
Переходная и импульсная функции
Слайд 12Форсирующее (дифференцирующее)
звено второго порядка
y(t) = (τ2p2+2ξτp+1)x(t), W(s) = τ2s2+2ξτs+1
Амплитудно-фазовая частотная характеристика
W(jω) = (1-ω2τ2) + j2ξωτ
Переходная и импульсная функции
Слайд 13Комбинации типовых звеньев
Дифференцирующее звено с замедлением
апериодическое звено
первого порядка
идеальное
дифференцирующее
звено
+
(Tp+1)
p(Tp+1) y(t) = x(t)
Уравнение и передаточная функция звена
Слайд 14Изодромное звено
форсирующее звено первого порядка
идеального интегрирующее звено
+
p y(t) =
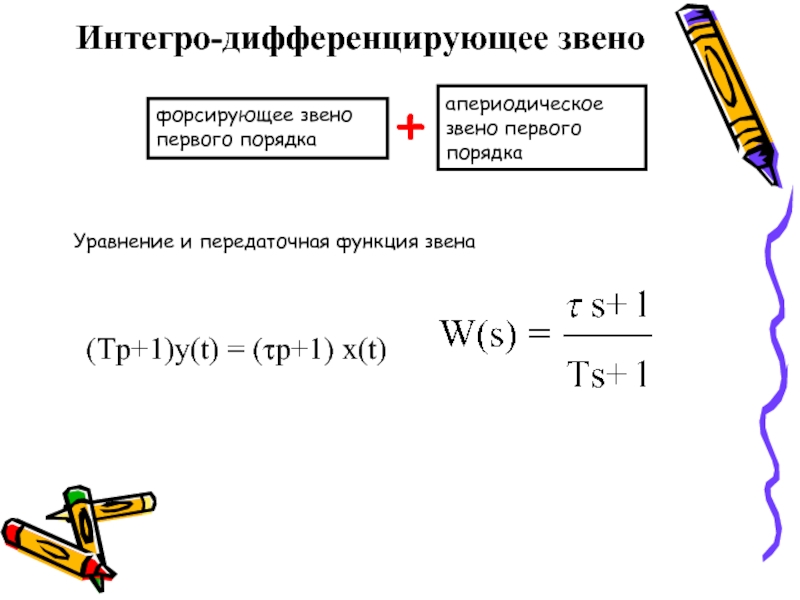
Слайд 15Интегро-дифференцирующее звено
апериодическое звено первого порядка
форсирующее звено первого порядка
+
(Tp+1)y(t) = (τp+1)
Уравнение и передаточная функция звена
Слайд 16Неминимально-фазовые звенья
звенья, которые, в отличие от обычных типовых звеньев, при равенстве
Звено с чистым запаздыванием
выходная величина повторяет входную с некоторой задержкой во времени
y(t) = x(t-τ),
τ - время чистого запаздывания
Амплитудно-фазовая частотная характеристика:
А(ω) = 1, ψ(ω)= −τω [рад]=
τω [угл.град]
Переходная и весовая функции
h(t) = 1(t-τ), w(t) = δ(t-τ)
линия связи, трубопровод,
транспортер, конвейер
Слайд 17Звено с положительным полюсом
Амплитудно-фазовая частотная характеристика
Здесь имеется положительный полюс
ψ(ω) = −π + arctg ωT
Слайд 18Звено с положительным нулем
W(s) = (1- τs)
Здесь имеется положительный
В нуле передаточная функция равна нулю (W(s)=0).
Амплитудно-фазовая частотная характеристика
W(jω) = (1 - jωτ )
ψ(ω) = - arctg ωτ