- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медицинская информатика - важная часть в изучении медицины презентация
Содержание
- 1. Медицинская информатика - важная часть в изучении медицины
- 2. Медицинская информатика — это научная дисциплина, занимающаяся исследованием
- 3. Роль медицинской информатики в научно-практическом обосновании и
- 4. Обработка информации в сложных системах Входные контролируемые
- 5. Изучаемые в медицине объекты являются сложными стохастическими
- 6. Для определения методов статистического анализа необходимо знать
- 7. Интенсивные показатели - показывают частоту явления в среде. В качестве
- 8. База данных На основе базы данных мы
- 9. научились строить матрицу корреляции,определили как связаны параметры нашей системы между собой
- 10. Мы сегодня на уроке освоили однофакторный регрессионый
- 11. освоили множественную регрессию. Множественная регрессия - это
- 12. Регрессия (regression) – зависимость среднего значения какой-либо
- 13. Линейная регрессия Пусть в ходе исследования были
Слайд 2Медицинская информатика — это научная дисциплина, занимающаяся исследованием процессов получения, передачи, обработки,
хранения, распространения, представления информации с использованием информационной техники и технологии в медицине и здравоохранении.
Предметом изучения медицинской информатики при этом будут являться информационные процессы, сопряженные с медико-биологическими, клиническими и профилактическими проблемами.
Объектом изучения МИ являются информационные технологии, реализуемые в здравоохранении.
Информационные технологии — это преимущественно компьютеризированные способы выработки, хранения, передачи и использования информации.
Предметом изучения медицинской информатики при этом будут являться информационные процессы, сопряженные с медико-биологическими, клиническими и профилактическими проблемами.
Объектом изучения МИ являются информационные технологии, реализуемые в здравоохранении.
Информационные технологии — это преимущественно компьютеризированные способы выработки, хранения, передачи и использования информации.
Слайд 3Роль медицинской информатики в научно-практическом обосновании и использовании современных технологий заключается
в нахождении новых решений на стыке формального и логического подходов с эмпирическим описательным характером медицины. Основой основ при работе с информацией является мышление и логический анализ. Именно они лежат в основе клинического диагноза - фиксированной на информационном носителе заключения врача о локализации, характере и стадию заболевания, которое обосновывает оптимальный выбор лечебной тактики (управляющей действия) в пределах имеющихся медицинских ресурсов.
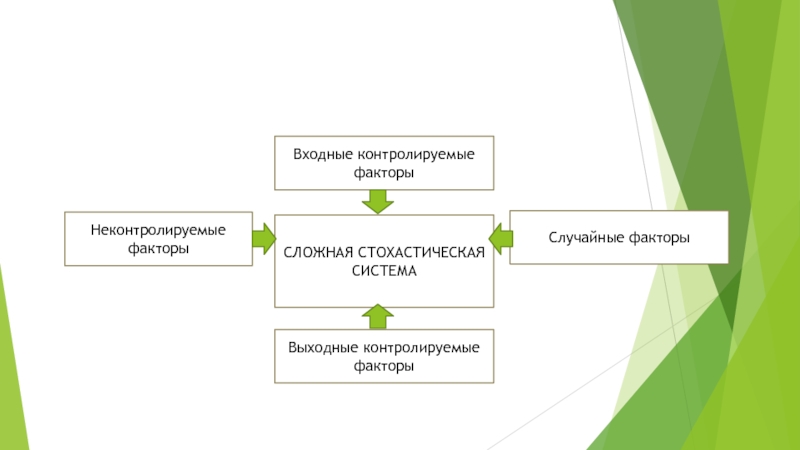
Слайд 4Обработка информации в сложных системах
Входные контролируемые факторы
СЛОЖНАЯ СТОХАСТИЧЕСКАЯ СИСТЕМА
Неконтролируемые факторы
Случайные факторы
Выходные
контролируемые факторы
Слайд 5Изучаемые в медицине объекты являются сложными стохастическими системами функционирующими при воздействии
на них множества входных факторов. Часть факторов Х1, Х2, …, Хk является контролируемыми. Другая часть относится к группе случайных факторов, оказывающих воздействие на систему.
Состояние системы характеризуется множеством выходных параметров Y1, Y2,…, Yl , которые также измеряются количественно или в баллах и представляют собой случайные величины, следующие какому-либо закону распределения с соответствующими числовыми характеристиками. В силу того, что неконтролируемые и случайные факторы для каждого объекта наблюдения принимают различные случайные значения, выходные параметры, характеризующие состояние и функционирование сложной стохастической (вероятностной) системы, являются случайными величинами, для исследования которых следует применять методы теории вероятности и математической статистики.
Количество входных контролируемых факторов и выходных параметров, описывающих объект исследования, определяется в зависимости от цели и задачи исследования.Так, например, для исследования связи между факторами тяжести состояния и факторами и параметрами, характеризующими эффективность лечения пострадавших с сочетанной механической травмой при ведущем повреждении головы, в качестве входных контролируемых факторов целесообразно иметь:
X1 – возраст, лет;
X2 –время доставки, ч;
X3 – частота пульса, уд/мин;
X4 – артериальное давление систолическое, мм.рт.ст.;
X5 – тип дыхания, в баллах: 1- нормальное, 2- частое, 3- патологическое;
Выходными параметрами могут быть:
Y1 – возникновение осложнений, в баллах: 0 – нет, 1 – есть;
Y2 – срок лечения, дней;
Y3 –исход лечения, в баллах: 0 – выжил, 1 – умер.
Состояние системы характеризуется множеством выходных параметров Y1, Y2,…, Yl , которые также измеряются количественно или в баллах и представляют собой случайные величины, следующие какому-либо закону распределения с соответствующими числовыми характеристиками. В силу того, что неконтролируемые и случайные факторы для каждого объекта наблюдения принимают различные случайные значения, выходные параметры, характеризующие состояние и функционирование сложной стохастической (вероятностной) системы, являются случайными величинами, для исследования которых следует применять методы теории вероятности и математической статистики.
Количество входных контролируемых факторов и выходных параметров, описывающих объект исследования, определяется в зависимости от цели и задачи исследования.Так, например, для исследования связи между факторами тяжести состояния и факторами и параметрами, характеризующими эффективность лечения пострадавших с сочетанной механической травмой при ведущем повреждении головы, в качестве входных контролируемых факторов целесообразно иметь:
X1 – возраст, лет;
X2 –время доставки, ч;
X3 – частота пульса, уд/мин;
X4 – артериальное давление систолическое, мм.рт.ст.;
X5 – тип дыхания, в баллах: 1- нормальное, 2- частое, 3- патологическое;
Выходными параметрами могут быть:
Y1 – возникновение осложнений, в баллах: 0 – нет, 1 – есть;
Y2 – срок лечения, дней;
Y3 –исход лечения, в баллах: 0 – выжил, 1 – умер.
Слайд 6Для определения методов статистического анализа необходимо знать характер, распределения и числовые
характеристики всех переменных, входящих в матрицу наблюдений. Наилучшие результаты многомерного статистического анализа данных медико-биологических исследований получают, когда распределения входных контролируемых факторов и выходных параметров нормальное или близкое к нему. Основными задачами статистического описания переменных являются:
определение числовых характеристик переменных и оценка их точности и надежности;
определение статистических рядов распределения переменных и оценки их соответствия теоретическим законам распределения;
оценка зависимости различия показателей в независимых и связанных выборках
По числовым характеристикам, таким, как среднее арифметическое значение, среднее квадратичное отклонение, средняя квадратичная ошибка среднего значения определяют доверительные интервалы, решаются задачи нормирования и оценивается значимость различий показателей в различных условиях. Статистический ряд распределения дает представление о виде распределения показателя в диапазоне полученных наблюдений и является основой для оценки его соответствия с тем или иным теоретическим законом распределения. Оценка значимости различия показателей в независимых и связанных выборках – одна из основных задач решаемых исследователями при сравнении методов профилактики, лечения различных заболеваний, состояния работоспособности сотрудников трудовых коллективов в различных условиях и в других подобных ситуациях. (устно)
определение числовых характеристик переменных и оценка их точности и надежности;
определение статистических рядов распределения переменных и оценки их соответствия теоретическим законам распределения;
оценка зависимости различия показателей в независимых и связанных выборках
По числовым характеристикам, таким, как среднее арифметическое значение, среднее квадратичное отклонение, средняя квадратичная ошибка среднего значения определяют доверительные интервалы, решаются задачи нормирования и оценивается значимость различий показателей в различных условиях. Статистический ряд распределения дает представление о виде распределения показателя в диапазоне полученных наблюдений и является основой для оценки его соответствия с тем или иным теоретическим законом распределения. Оценка значимости различия показателей в независимых и связанных выборках – одна из основных задач решаемых исследователями при сравнении методов профилактики, лечения различных заболеваний, состояния работоспособности сотрудников трудовых коллективов в различных условиях и в других подобных ситуациях. (устно)
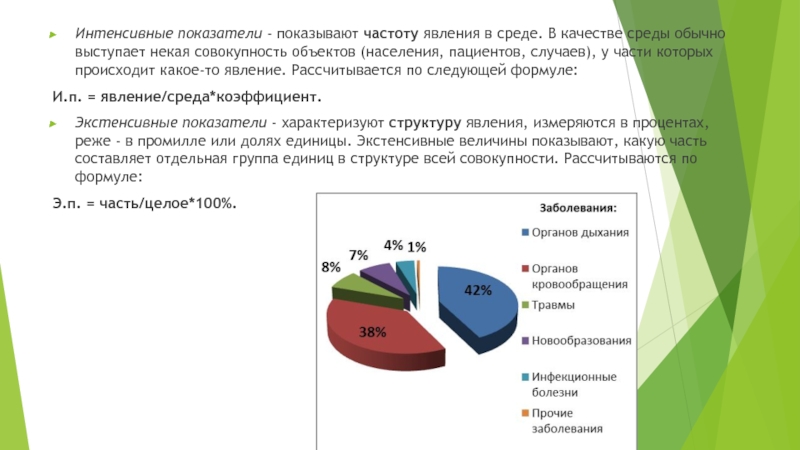
Слайд 7Интенсивные показатели - показывают частоту явления в среде. В качестве среды обычно выступает некая
совокупность объектов (населения, пациентов, случаев), у части которых происходит какое-то явление. Рассчитывается по следующей формуле:
И.п. = явление/среда*коэффициент.
Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах, реже - в промилле или долях единицы. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по формуле:
Э.п. = часть/целое*100%.
И.п. = явление/среда*коэффициент.
Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах, реже - в промилле или долях единицы. Экстенсивные величины показывают, какую часть составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по формуле:
Э.п. = часть/целое*100%.
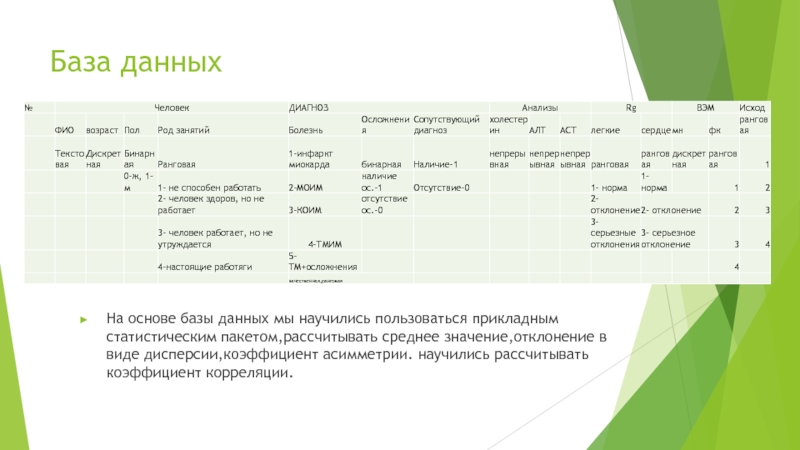
Слайд 8База данных
На основе базы данных мы научились пользоваться прикладным статистическим пакетом,рассчитывать
среднее значение,отклонение в виде дисперсии,коэффициент асимметрии. научились рассчитывать коэффициент корреляции.
Слайд 9научились строить матрицу корреляции,определили как связаны параметры нашей системы между собой
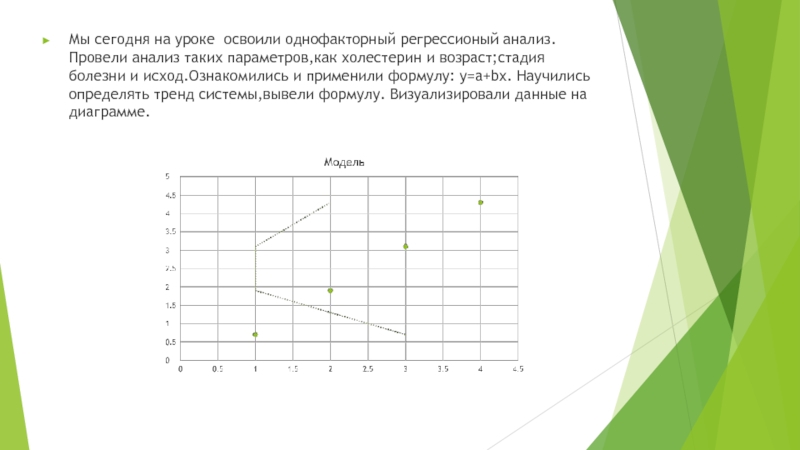
Слайд 10Мы сегодня на уроке освоили однофакторный регрессионый анализ. Провели анализ таких
параметров,как холестерин и возраст;стадия болезни и исход.Ознакомились и применили формулу: y=a+bx. Научились определять тренд системы,вывели формулу. Визуализировали данные на диаграмме.
Слайд 11освоили множественную регрессию. Множественная регрессия - это статистическая процедура изучения зависимости,
существующее между зависимой переменной и несколькими независимыми переменными. Моделировали зависимость между возрастом, функцией, мощностью, холестерином и исходом .
Слайд 12Регрессия (regression) – зависимость среднего значения какой-либо случайной величины от некоторой
другой величины или от нескольких величин
Случайная величина, выполняющая роль независимой переменной в регрессионной модели называется регрессионной переменной или ( регрессором )
Выбор функции (модели), как правило, определяется теоретическими соображениями, а также по распределению экспериментальных значений (x,y) на диаграмме рассеяния
Наиболее важным является случай, когда регрессия является линейной
Случайная величина, выполняющая роль независимой переменной в регрессионной модели называется регрессионной переменной или ( регрессором )
Выбор функции (модели), как правило, определяется теоретическими соображениями, а также по распределению экспериментальных значений (x,y) на диаграмме рассеяния
Наиболее важным является случай, когда регрессия является линейной
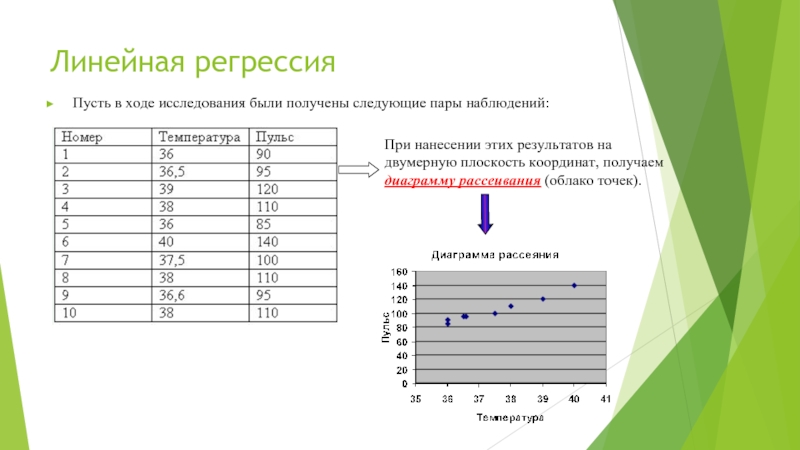
Слайд 13Линейная регрессия
Пусть в ходе исследования были получены следующие пары наблюдений:
При нанесении
этих результатов на двумерную плоскость координат, получаем диаграмму рассеивания (облако точек).