- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Жазықтықтағы және кеңістіктегі тікбұрышты координаталар. Векторлар және оларға қолданылатын сызықтық амалдар презентация
Содержание
- 1. Жазықтықтағы және кеңістіктегі тікбұрышты координаталар. Векторлар және оларға қолданылатын сызықтық амалдар
- 2. Жоспары: Вектор шамалар ұғымы. Оларды қосу,
- 3. Векторларды қосу a және b векторларының a+b
- 4. Бұл схеманы параллелограммға дейін толықтырамыз: a+b қосындысы,
- 5. Векторларды алу a және b векторларының a
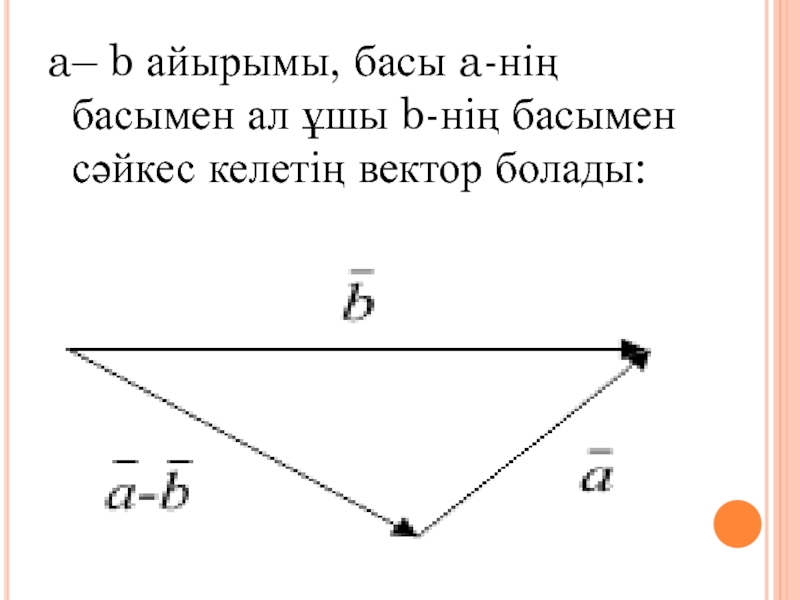
- 6. a– b айырымы, басы a-нің басымен ал ұшы b-нің басымен сәйкес келетің вектор болады:
- 7. Скаляр көбейтіндісі Аңықтама. a және b
- 8. Скаляр көбейтіндінің қасиеттері: 1). (a, b) =
- 9. Скаляр көбейтіндісінің геометрикалық интерпретациясы. a және b
- 10. Векторлардың вектор көбейтіндісі. a векторы мен
- 11. ВЕКТОРЛАРДЫҢ АРАЛАС КӨБЕЙТІНДІСІ Егер біз және векторларын скалярлық түрде көбейтсек, оның нәтижесі сан болады. Осы санды үшінші
Слайд 1Тақырыбы: Жазықтықтағы және кеңістіктегі тікбұрышты координаталар Векторлар және оларға қолданылатын сызықтық амалдар.
Слайд 2Жоспары:
Вектор шамалар ұғымы. Оларды қосу, алу, санға көбейту.
Векторлардың скаляр көбейтіндісі.
Векторлардың вектор
Слайд 3Векторларды қосу
a және b векторларының a+b қосындысын параллелограмм ережесі бойынша есептеуге
Бұл үшін бұл векторларды сызайық:
a+b қосындысын есептеу табу үшін a -нің ұшына b -нің басын орналастырамыз:
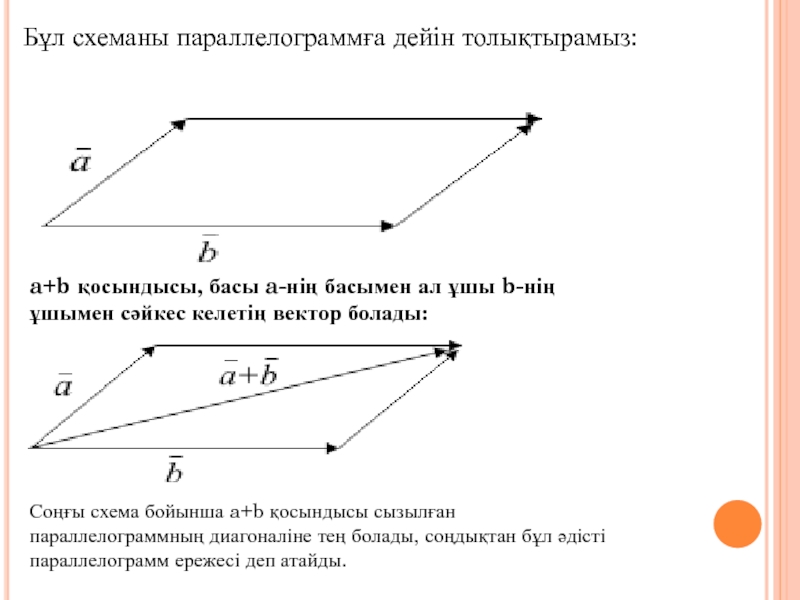
Слайд 4Бұл схеманы параллелограммға дейін толықтырамыз:
a+b қосындысы, басы a-нің басымен ал ұшы
Соңғы схема бойынша a+b қосындысы сызылған параллелограммның диагоналіне тең болады, соңдықтан бұл әдісті параллелограмм ережесі деп атайды.
Слайд 5Векторларды алу
a және b векторларының a – b айырымын есептеу үшін
Бұл үшін бұл векторларды сызайық:
a -нің және b -нің ұштарын біріктірейік:
Слайд 7Скаляр көбейтіндісі
Аңықтама.
a және b векторларының (a, b) скаляр көбейтіндісі деп ax·
(a, b) = ax · bx+ay · by
Мысалы a = {1, 3}, b = {4, 2} болса, онда (a, b) = 1·4+3·2 = 4+6 = 10.
Слайд 8Скаляр көбейтіндінің қасиеттері:
1). (a, b) = (b, a)
2). (a, a) =
3). (a+b, c) = (a, c) + (b, c)
4). (a –b, c) = (a, c) -(b, c)
5). (k ·a, b) = (a, k ·b)=k ·(a, b)
Слайд 9Скаляр көбейтіндісінің геометрикалық интерпретациясы.
a және b векторларының (a, b) скаляр көбйтіндісі
Яғни (a, b) =|a| · |b| cos∠(a, b),
мұндағы ∠(a, b) дегеніміз a және b векторларының арасындағы бұрыш:
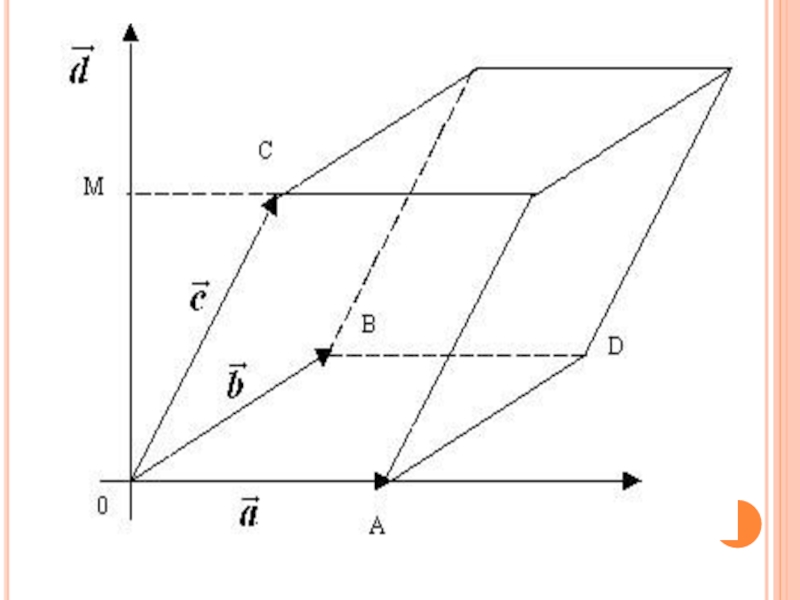
Слайд 10Векторлардың вектор көбейтіндісі.
a векторы мен b векторының R кеңістігіндегі векторлық көбейтіндісі
c векторы әр a және b векторларына ортогональ ;
c векторыны abc векторлар үштігі оң болатындай бағытталған;
R кеңістігі үшін a,b,c векторлар үштігінің ассоциативтігі орындалу қажет.
Слайд 11ВЕКТОРЛАРДЫҢ АРАЛАС КӨБЕЙТІНДІСІ
Егер біз және векторларын скалярлық түрде көбейтсек, оның нәтижесі сан болады. Осы санды үшінші векторына көбейтсек, онда векторына коллинеарлы вектор шығады.
Егер және векторларының векторлық көбейтіндісін тапсақ, онда жаңа
Векторлы- скалярлық көбейтіндіні аралас көбейтінді деп атап, оны былай белгілейді: немесе
Енді осы біз , , векторларының аралас көбейтінділерінің геометриялық мағынасын анықтайық: