- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Законы распределения случайных величин презентация
Содержание
- 1. Законы распределения случайных величин
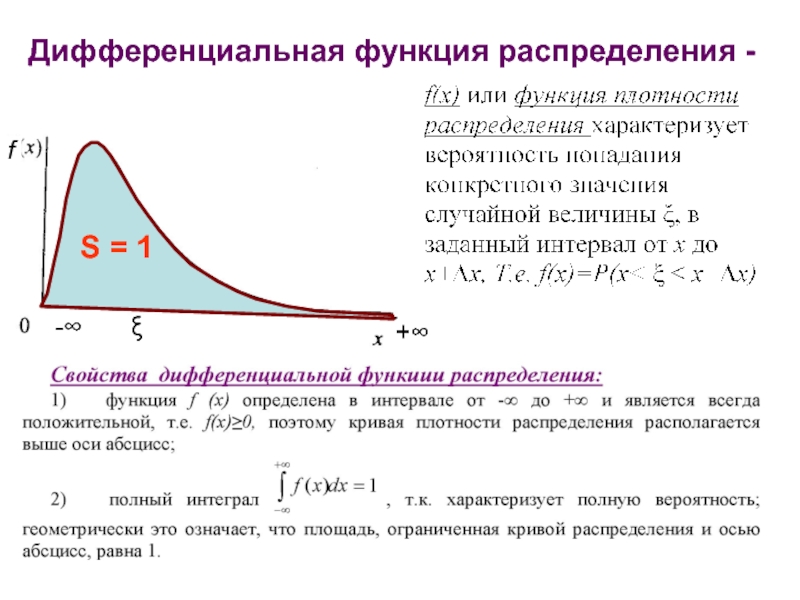
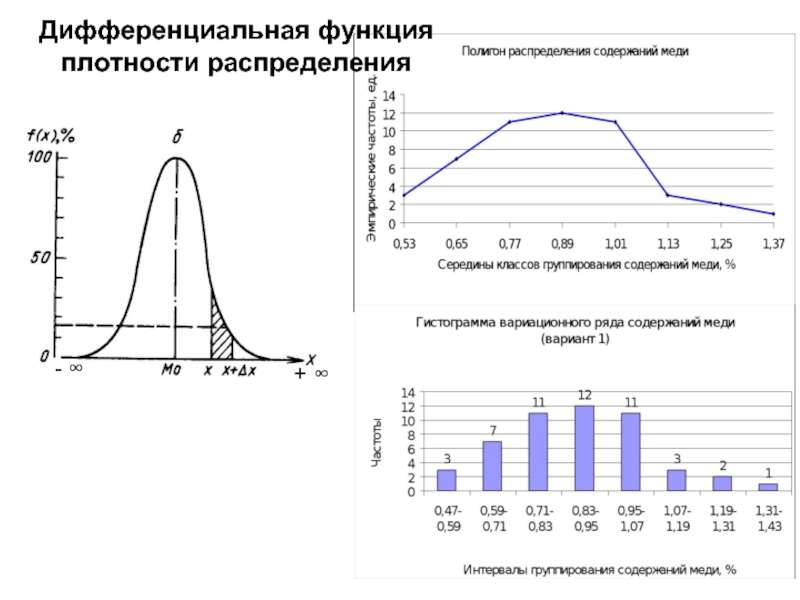
- 2. Дифференциальная функция (закон) плотности распределения
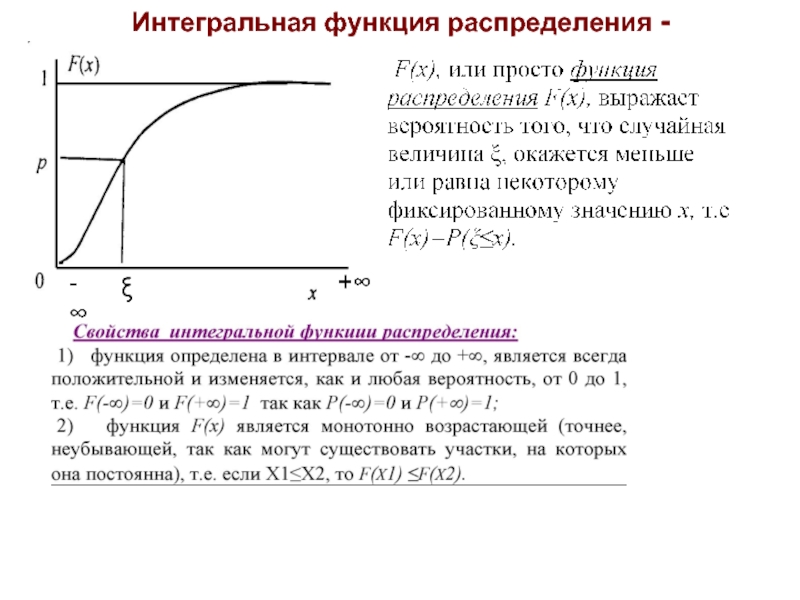
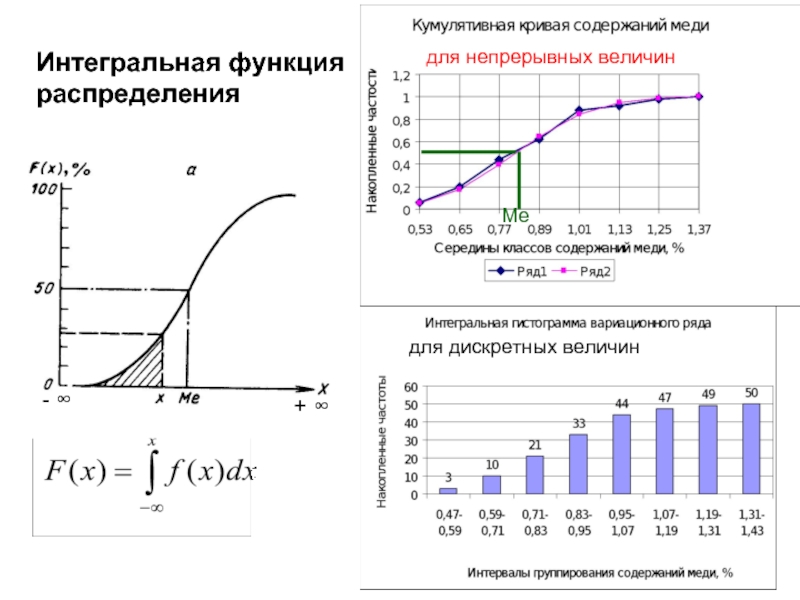
- 3. Интегральная функция распределения -
- 4. Интегральная функция распределения + ∞ - ∞
- 5. Дифференциальная функция распределения - -∞ +∞ ξ f S = 1
- 6. Дифференциальная функция плотности распределения - ∞ + ∞
- 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ТЕОРЕТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
- 11. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ В ГЕОЛОГИИ
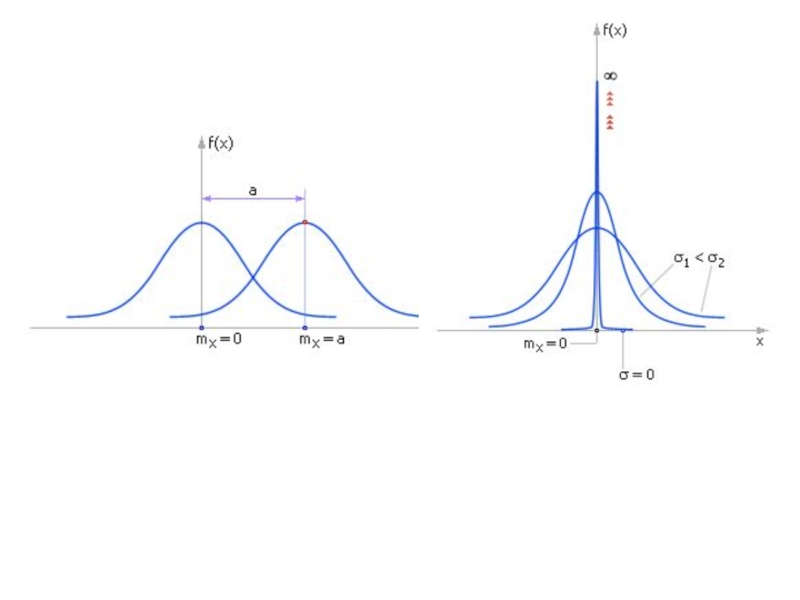
- 12. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
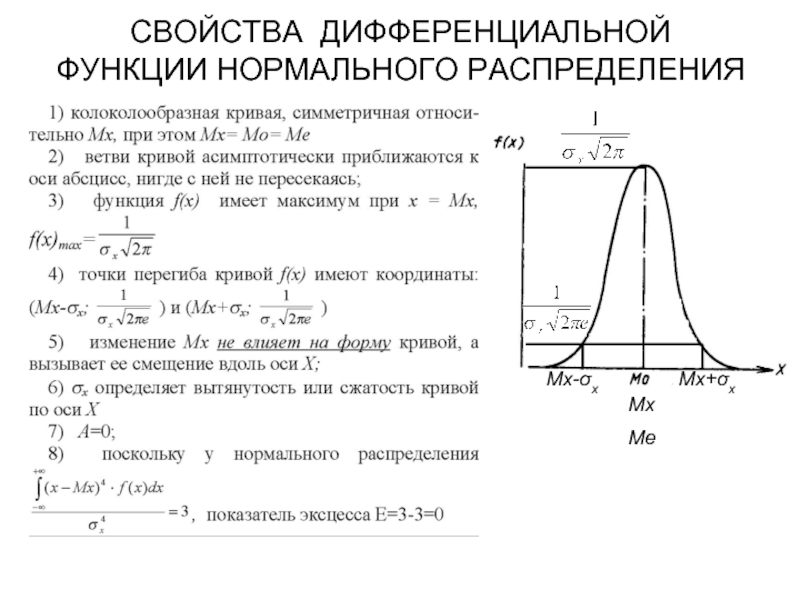
- 13. СВОЙСТВА ДИФФЕРЕНЦИАЛЬНОЙ ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ Мх Ме Мх-σх Мх+σх
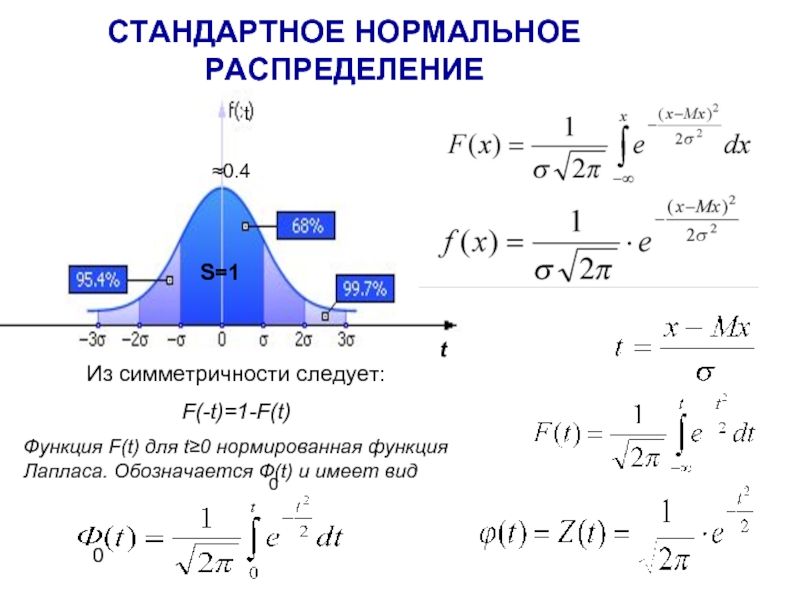
- 15. СТАНДАРТНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Из симметричности следует: F(-t)=1-F(t)
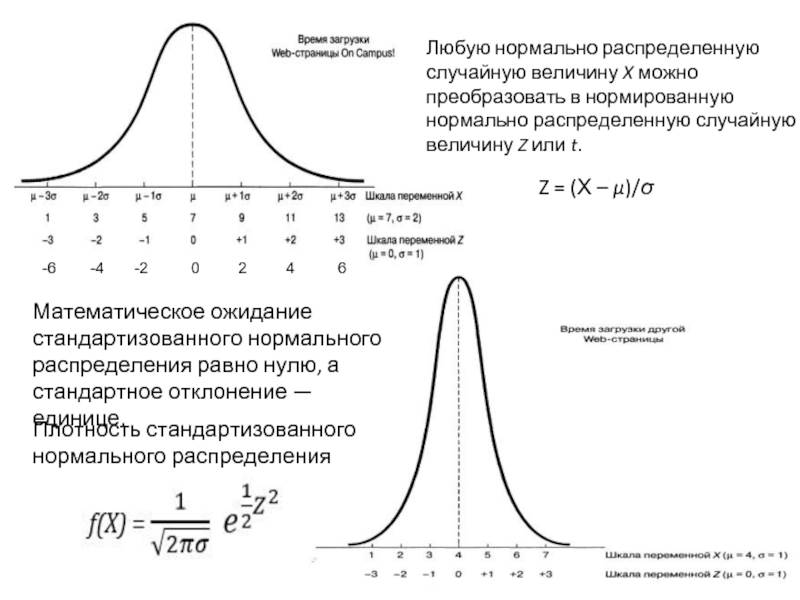
- 16. Z = (Х – μ)/σ Любую нормально
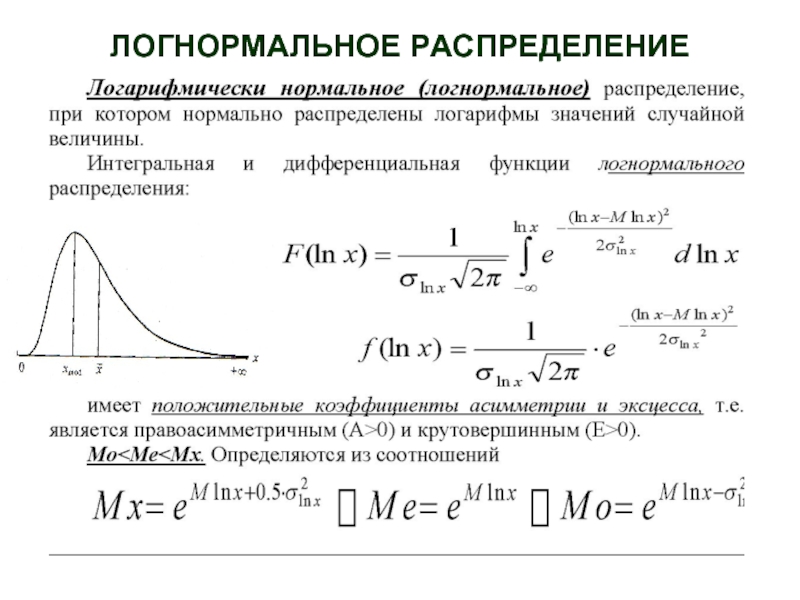
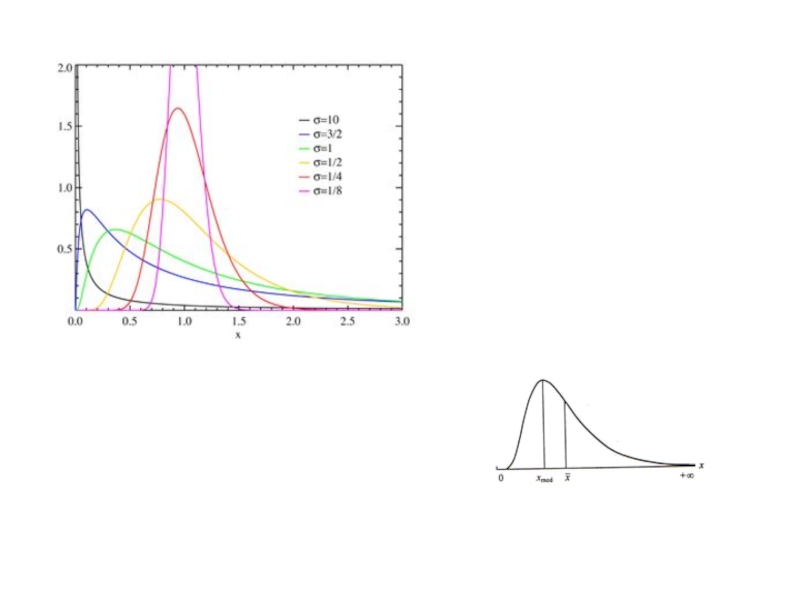
- 17. ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 19. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ
- 20. Критерий Пирсона χ2
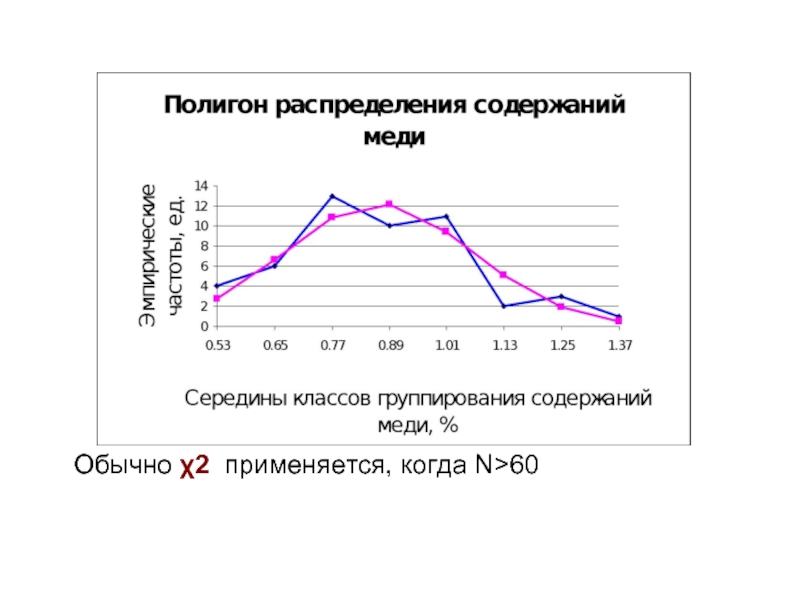
- 21. Обычно χ2 применяется, когда N>60
- 23. Критерий Колмогорова λ
Дифференциальная функция (закон) плотности распределения Интегральная функция (закон) распределения + ∞ - ∞ - ∞ + ∞
Слайд 2
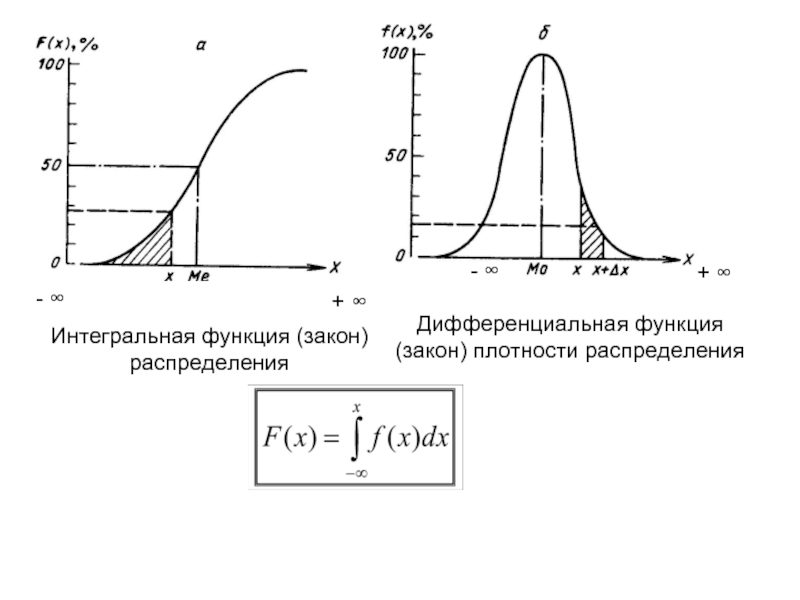
Дифференциальная функция (закон) плотности распределения
Интегральная функция (закон) распределения
+ ∞
- ∞
- ∞
+
∞
Слайд 15СТАНДАРТНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Из симметричности следует:
F(-t)=1-F(t)
Функция F(t) для t≥0 нормированная функция Лапласа.
Обозначается Ф(t) и имеет вид
t
t
0
0
≈0.4
S=1
Слайд 16Z = (Х – μ)/σ
Любую нормально распределенную случайную величину X можно
преобразовать в нормированную нормально распределенную случайную величину Z или t.
Математическое ожидание стандартизованного нормального распределения равно нулю, а стандартное отклонение — единице.
Плотность стандартизованного нормального распределения
-6 -4 -2 0 2 4 6
