многочлен Лагранжа. Схема Эйткена
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3) презентация
Содержание
- 1. Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)
- 2. Задача аппроксимации Задача аппроксимации состоит в приближенной
- 3. Постановка задачи интерполяции Пусть функция y =
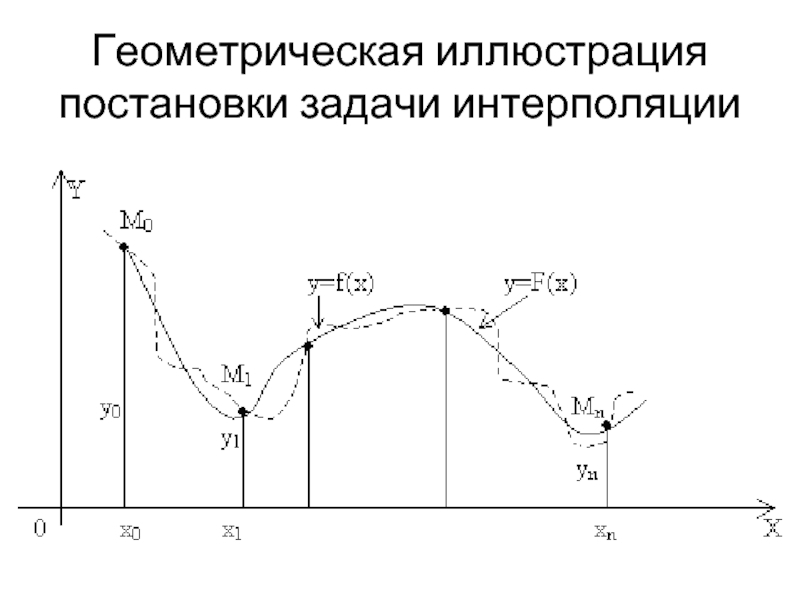
- 4. Геометрическая иллюстрация постановки задачи интерполяции
- 5. Применение интерполяции 1) интерполяция используется в тех
- 6. Применение интерполяции 2) интерполяция используется при решении
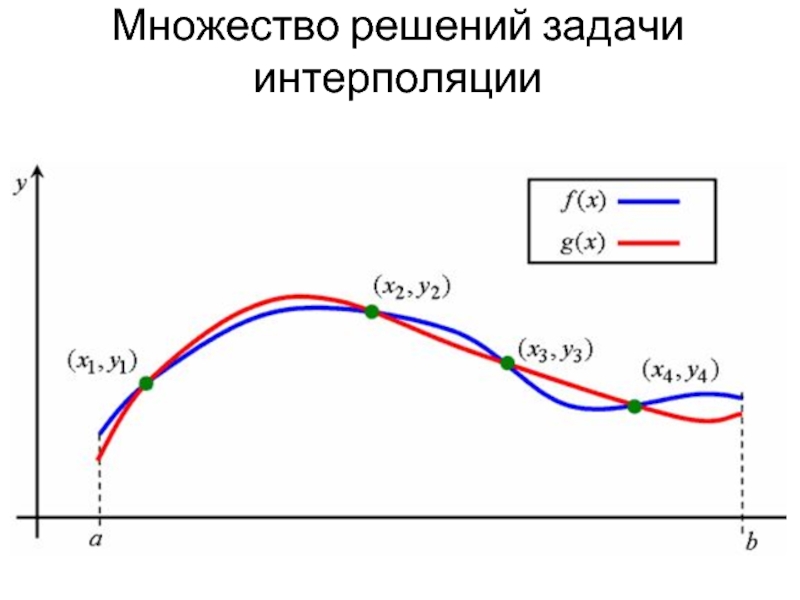
- 7. Множество решений задачи интерполяции
- 8. Виды интерполяции
- 9. Постановка задачи параболической интерполяции Функция y =
- 10. Единственность интерполяционного многочлена
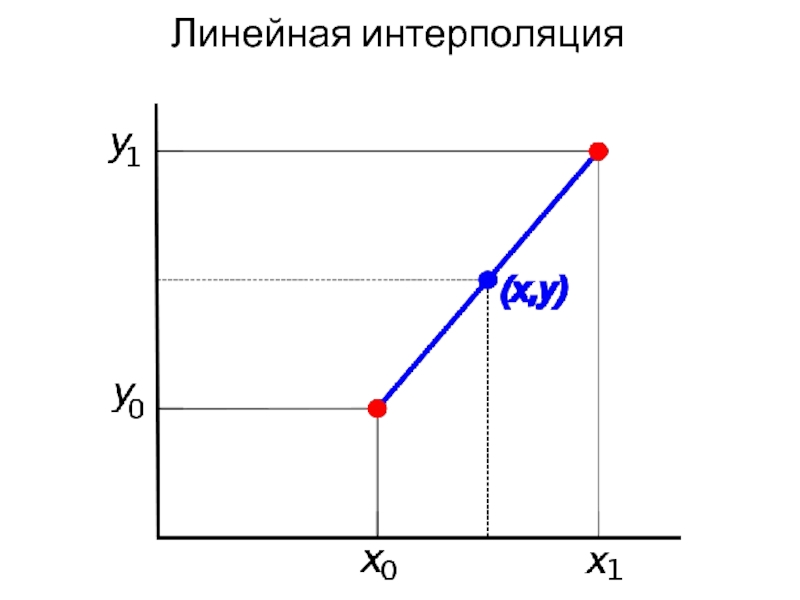
- 11. Линейная интерполяция
- 12. Пример построения интерполяционного многочлена непосредственным решением СЛУ
- 13. Интерполяционная формула Лагранжа
- 14. Интерполяционная формула Лагранжа
- 15. Интерполяционная формула Лагранжа Полученная формула называется интерполяционным
- 16. Формулы Лагранжа для линейной и квадратичной интерполяции
- 17. Пример использования формулы Лагранжа Пусть интерполируемая функция
- 18. Интерполяционная схема Эйткена ………………………………………………………………………………………………………
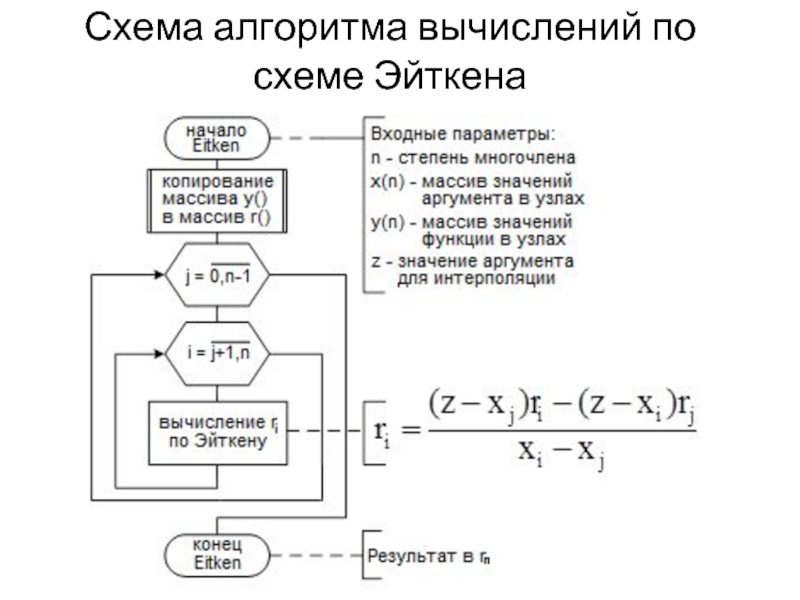
- 19. Схема алгоритма вычислений по схеме Эйткена
Слайд 1Лекция 3
Постановка задачи. Применение интерполяции
Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена
Интерполяционный
Слайд 2Задача аппроксимации
Задача аппроксимации состоит в приближенной замене функции f(x), заданной таблично,
на некоторую функцию ϕ(х) так, чтобы отклонение ϕ(х) от f(x) в некоторой области удовлетворяло заданному условию. Функция ϕ(х) называется аппроксимирующей функцией.
В качестве аппроксимирующей функции часто используют алгебраический многочлен вида:
ϕn(x) = a0 + a1x + a2x2 + … + anxn
В этом случае говорят о параболической аппроксимации.
Интерполяция является важным частным случаем аппроксимации.
В качестве аппроксимирующей функции часто используют алгебраический многочлен вида:
ϕn(x) = a0 + a1x + a2x2 + … + anxn
В этом случае говорят о параболической аппроксимации.
Интерполяция является важным частным случаем аппроксимации.
Слайд 3Постановка задачи интерполяции
Пусть функция y = f(x) задана таблицей значений в
n+1 точке:
так, что y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти функцию F(x), приближающую функцию f(x) (f(x) = F(x) + R(x), где R(x) – погрешность интерполяции), совпадающую с функцией f(x) в точках xi (i=0, 1, 2, …n). Функция f(x) называется интерполируемой, F(x) – интерполирующей, точки xi (i=0, 1, 2, …n) – узлами интерполяции.
так, что y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти функцию F(x), приближающую функцию f(x) (f(x) = F(x) + R(x), где R(x) – погрешность интерполяции), совпадающую с функцией f(x) в точках xi (i=0, 1, 2, …n). Функция f(x) называется интерполируемой, F(x) – интерполирующей, точки xi (i=0, 1, 2, …n) – узлами интерполяции.
Слайд 5Применение интерполяции
1) интерполяция используется в тех случаях, когда интерполируемая функция известна
лишь при некоторых дискретных значениях аргумента xi, а требуется получить ее приближенные значения в других точках x≠ xi:
если f(xi) – результаты эксперимента (измерений);
если f(xi) – результаты сложных вычислений на компьютере, например, результаты имитационного моделирования;
если f(xi) – табличные значения некоторой элементарной или специальной функции, а требуется получить таблицу с меньшим шагом или значение функции при x≠ xi.
если f(xi) – результаты эксперимента (измерений);
если f(xi) – результаты сложных вычислений на компьютере, например, результаты имитационного моделирования;
если f(xi) – табличные значения некоторой элементарной или специальной функции, а требуется получить таблицу с меньшим шагом или значение функции при x≠ xi.
Слайд 6Применение интерполяции
2) интерполяция используется при решении ряда других задач вычислительной математики:
приближенное
нахождение корня уравнения f(x) = 0 методом обратной интерполяции;
численное дифференцирование и интегрирование функции f(x);
приближенное определение экстремума функции f(x).
численное дифференцирование и интегрирование функции f(x);
приближенное определение экстремума функции f(x).
Слайд 9Постановка задачи параболической интерполяции
Функция y = f(x) задана таблицей значений в
n+1 точке:
y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти многочлен Pn(x) степени n, значения которого
Pn(xi) = f(xi), i=0, 1, 2, … n.
y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти многочлен Pn(x) степени n, значения которого
Pn(xi) = f(xi), i=0, 1, 2, … n.
Слайд 15Интерполяционная формула Лагранжа
Полученная формула называется интерполяционным многочленом Лагранжа. Несмотря на некоторую
громоздкость, одним из преимуществ формулы Лагранжа является возможность ее записи непосредственно по заданной таблице значений функции. При этом следует учитывать следующие правила:
формула содержит столько слагаемых, сколько узлов в таблице;
каждое слагаемое – это произведение дробного коэффициента на соответствующее значение yi;
числитель коэффициента при yi содержит произведение разностей х со всеми узлами кроме xi, а знаменатель полностью повторяет числитель при подстановке х = xi.
формула содержит столько слагаемых, сколько узлов в таблице;
каждое слагаемое – это произведение дробного коэффициента на соответствующее значение yi;
числитель коэффициента при yi содержит произведение разностей х со всеми узлами кроме xi, а знаменатель полностью повторяет числитель при подстановке х = xi.
Слайд 17Пример использования формулы Лагранжа
Пусть интерполируемая функция f(x) задана той же таблицей,
что и в предыдущем разделе. Требуется найти приближенное значение функции в точке x = 0.5 путем квадратичной интерполяции.