плоскостей.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей презентация
Содержание
- 1. Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей
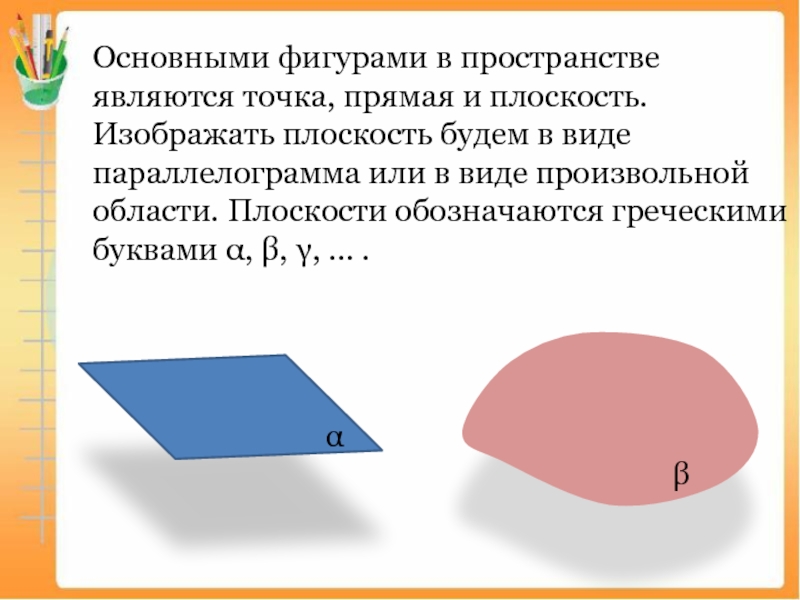
- 2. Основными фигурами в пространстве являются точка, прямая
- 3. Взаимное расположение прямых в пространстве: Пересекаются Параллельны Скрещиваются
- 4. Пересекающиеся прямые в пространстве: M Определение:
- 5. Параллельные прямые в пространстве: Определение: Прямые называются
- 6. Скрещивающиеся прямые: Определение: Прямые называются скрещивающимися, если они не лежат в одной плоскости.
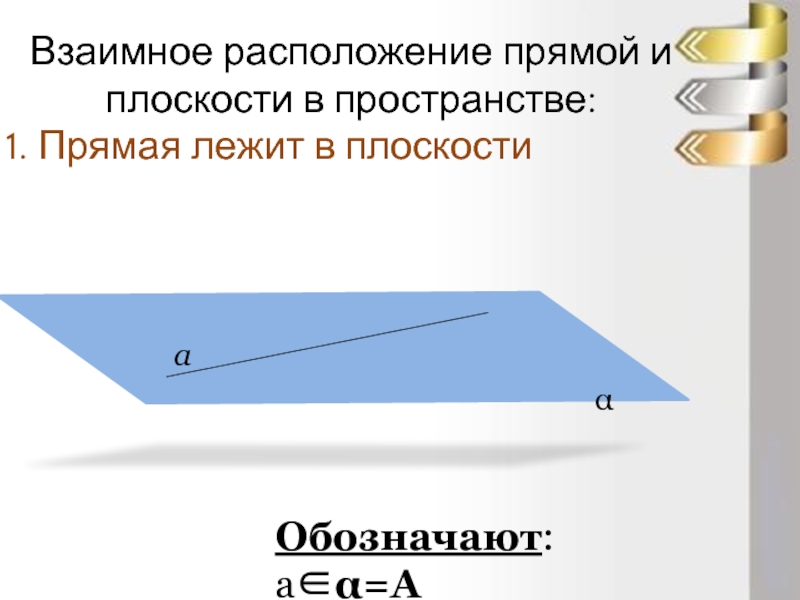
- 7. Взаимное расположение прямой и плоскости в пространстве: Прямая лежит в плоскости Обозначают: а∈α=A
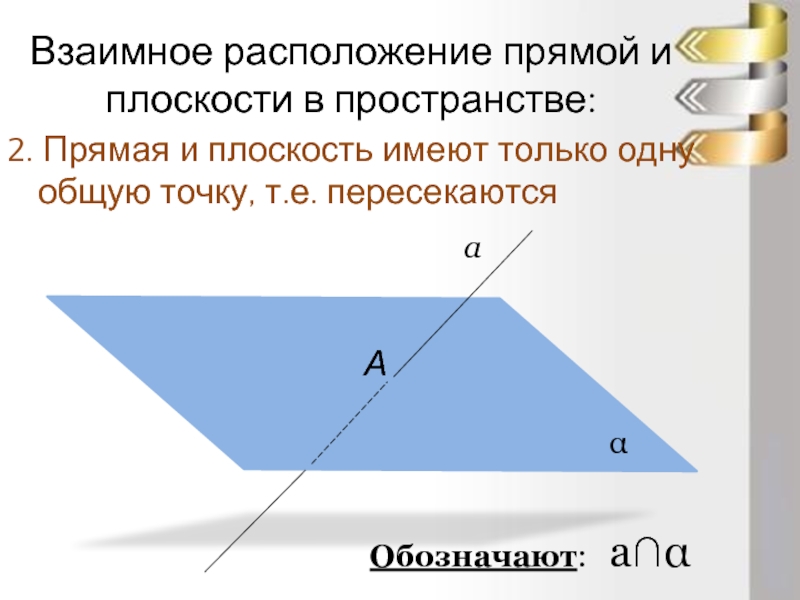
- 8. Взаимное расположение прямой и плоскости в пространстве:
- 9. Взаимное расположение прямой и плоскости в пространстве:
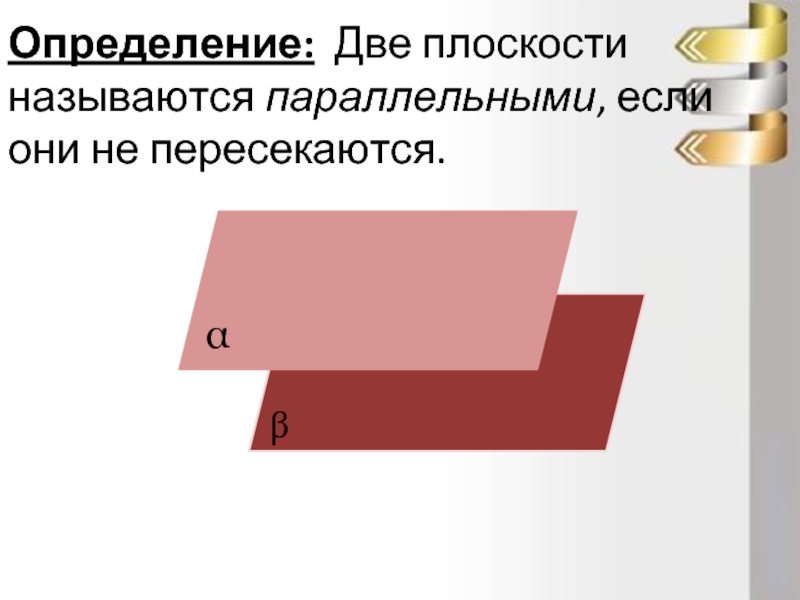
- 10. Определение: Две плоскости называются параллельными, если они не пересекаются.
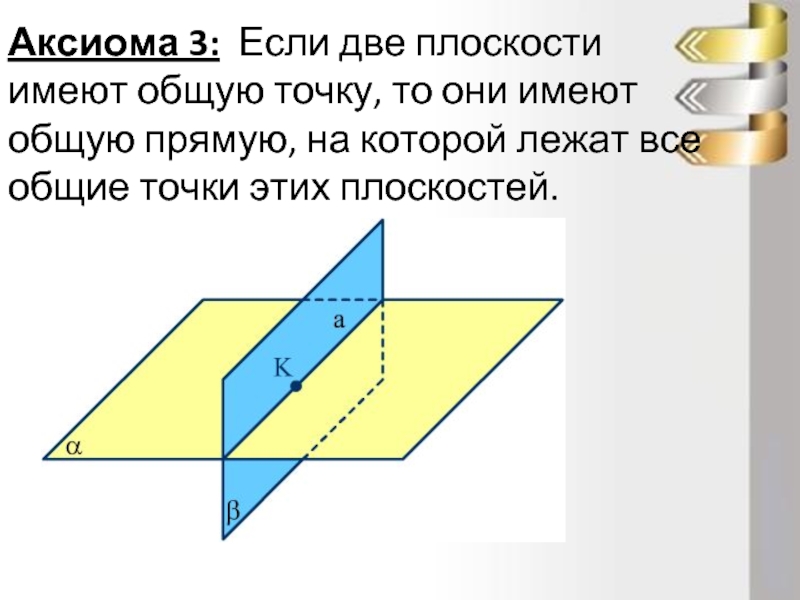
- 11. Аксиома 3: Если две плоскости имеют общую
- 12. Задача №1 На рисунке точки M,
- 13. Задача №2 Точка С лежит на отрезке
- 14. Задача №3 Точка D не лежит
- 15. Задача №4 Точка В не лежит в
- 16. Домашнее задание: №№ 5 и 6 Выучить записи в тетради (подготовиться к проверочной работе)
Основными фигурами в пространстве являются точка, прямая и плоскость.
Изображать плоскость будем в виде параллелограмма или в виде произвольной области. Плоскости обозначаются греческими буквами α, β, γ, … .
Слайд 1Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность
Слайд 2Основными фигурами в пространстве являются точка, прямая и плоскость. Изображать плоскость будем
в виде параллелограмма или в виде произвольной области. Плоскости обозначаются греческими буквами α, β, γ, … .
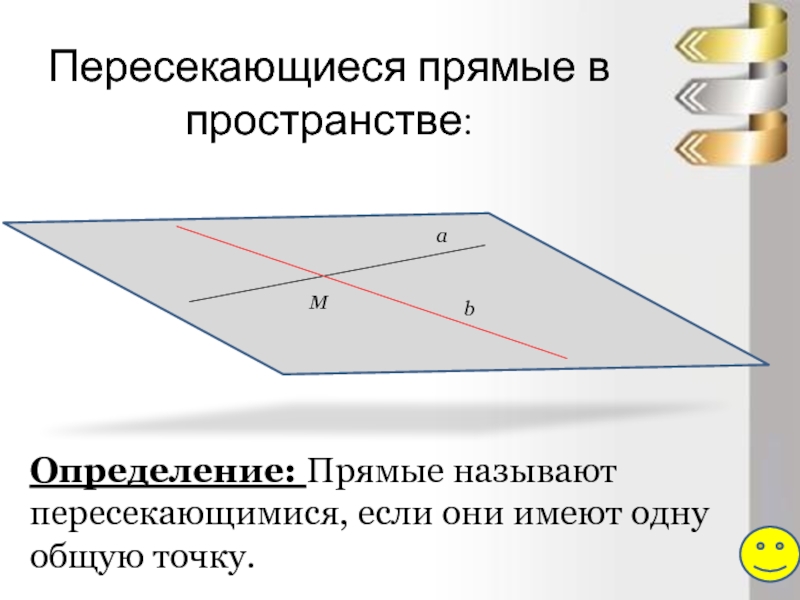
Слайд 4Пересекающиеся прямые в пространстве:
M
Определение: Прямые называют пересекающимися, если они имеют одну
общую точку.
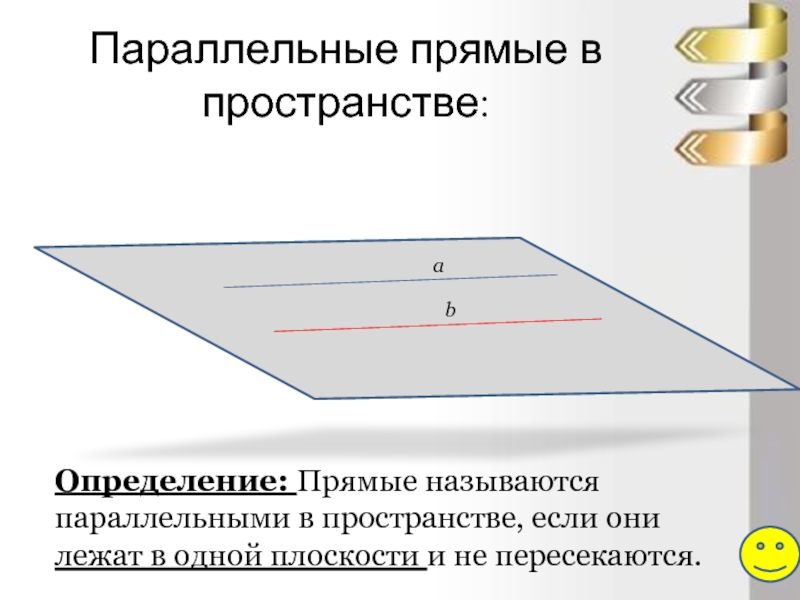
Слайд 5Параллельные прямые в пространстве:
Определение: Прямые называются параллельными в пространстве, если они
лежат в одной плоскости и не пересекаются.
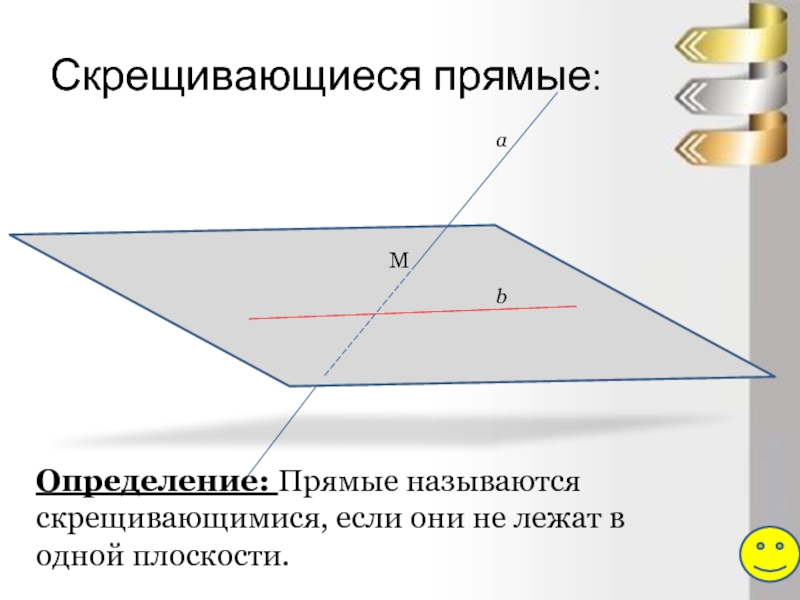
Слайд 6Скрещивающиеся прямые:
Определение: Прямые называются скрещивающимися, если они не лежат в одной
плоскости.
Слайд 7Взаимное расположение прямой и плоскости в пространстве:
Прямая лежит в плоскости
Обозначают:
а∈α=A
Слайд 8Взаимное расположение прямой и плоскости в пространстве:
2. Прямая и плоскость имеют
только одну общую точку, т.е. пересекаются
Обозначают: а∩α
Слайд 9Взаимное расположение прямой и плоскости в пространстве:
3. Прямая и плоскость не
имеют ни одной общей точки
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. (обозначают: а⏐⏐α).
Слайд 11Аксиома 3: Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
Слайд 12Задача №1 На рисунке точки M, N, Q и Р –
середины отрезков DB, DC, AC и AB. Найдите периметр четырехугольника MNQP, если AD=12см, BC=14 см.
Слайд 13Задача №2 Точка С лежит на отрезке АВ. Через точку А проведена
плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках . Найдите длину отрезка , если АС:СВ=3:2 и ВВ1=20 см.
Слайд 14Задача №3 Точка D не лежит в плоскости треугольника АВС, точки
M, N и Р – середины отрезков DA, DB и DC соответственно, точка К лежит на отрезке BN. Выясните взаимное расположение прямых:
а) ND и AB;
б) MN и AB;
в) KN и AC;
г) MD и BC.
Слайд 15Задача №4 Точка В не лежит в плоскости треугольника ADC, точки M,N
и Р- середины отрезков BA, BC и BD соответственно.
а) Докажите, что плоскости MNP и ADC параллельны.
б) Найдите площадь треугольника
MNP, если площадь
треугольника ADC равна 48 см2.
