- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выведение формулы золотого сечения презентация
Содержание
- 1. Выведение формулы золотого сечения
- 2. Пифагор Самосский Пифагор — древнегреческий философ, математик
- 3. «Золотой треугольник» В простейшем прямоугольном треугольнике с
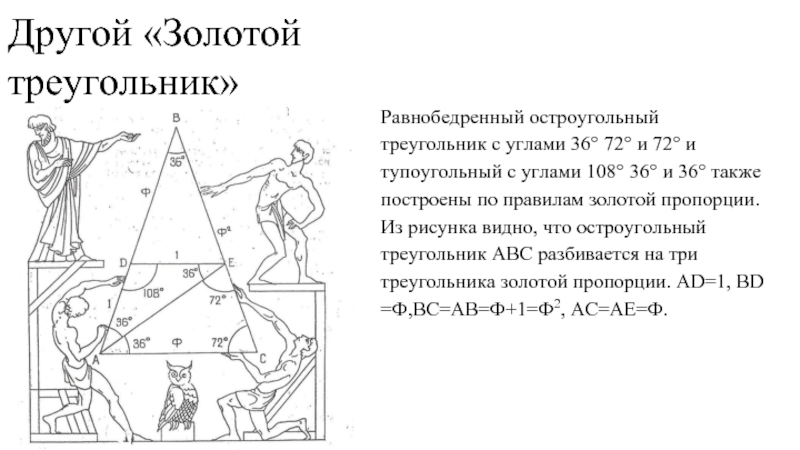
- 4. Другой «Золотой треугольник» Равнобедренный остроугольный треугольник
- 5. Связь с числом π Также интересен п/у
- 6. Ряд чисел Фибоначчи Появился он в ходе
- 7. Инвариантом золотого сечения явился ряд чисел
- 8. Ряд Люка
Слайд 2Пифагор Самосский
Пифагор — древнегреческий философ, математик и мистик. Родился в 570
Бюст Пифагора в Капитолийском музее в Риме
Слайд 3«Золотой треугольник»
В простейшем прямоугольном треугольнике с соотношением катетов 1:2 по теореме
Число «пять» у пифагорейцев считалось священным .
Соотношения сторон a, b, c данного треугольника: a/b=1:2, c/a=√5/1, c/b=√5/2,из них следует ещё одно соотношение (a+c)/b; равное 1,618033, которое и является Золотой пропорцией. Чаще её обозначают буквой Ф.
Таким образом, хорошо известный в древнем мире простой прямоугольный треугольник с отношением катетов 1:2 мог послужить основой для открытия теоремы квадратов, золотой пропорции и несоизмеримых величин — великих открытий Пифагора.
Слайд 4Другой «Золотой треугольник»
Равнобедренный остроугольный треугольник с углами 36° 72° и 72°
Слайд 5Связь с числом π
Также интересен п/у треугольник с углами 90° 54°
В той формуле дважды встречается чило «пять». И угол 36° является углом при вершинах пятиконечного звёздчатого многоугольника
Слайд 6Ряд чисел Фибоначчи
Появился он в ходе решения задачи из книги «Liber
Леонардо Пизанский Фибоначчи
Слайд 7
Инвариантом золотого сечения явился ряд чисел Фибоначчи 1, 2, 3, 5,
U1, U2 , U3, где Un= Un-1+ Un-2.