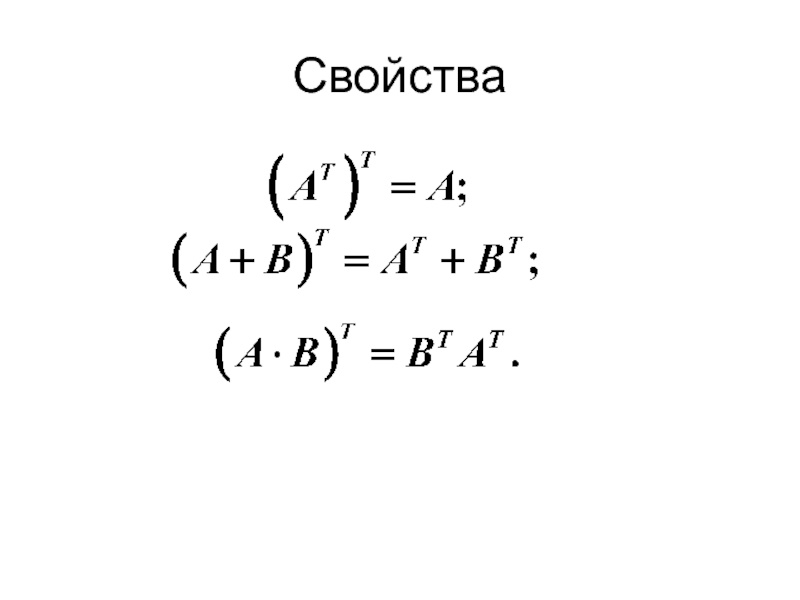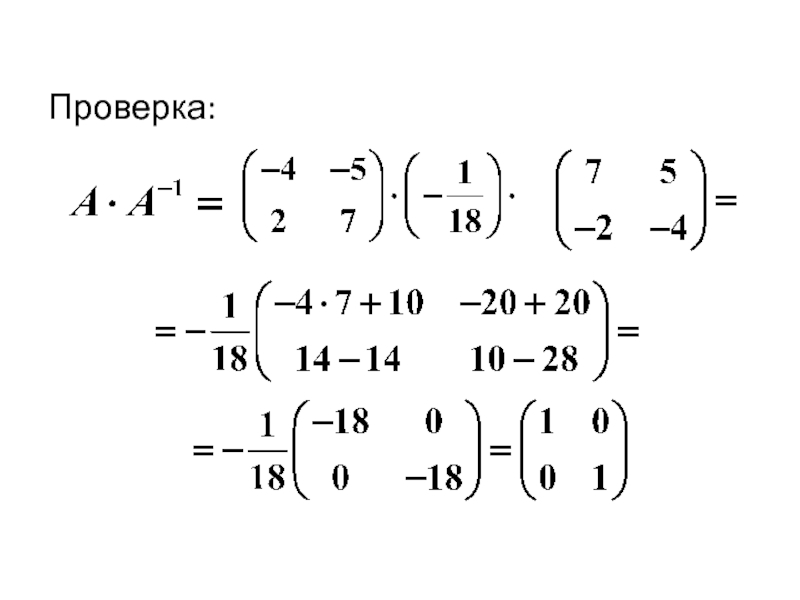- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 1 семестр презентация
Содержание
- 1. Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 1 семестр
- 2. Литература Дымков М.П., Конюх А.В., Майоровская С.В.,
- 6. Тема 1: Элементы линейной алгебры §1. Матрицы
- 7. Понятие матрицы и основанный на нем раздел
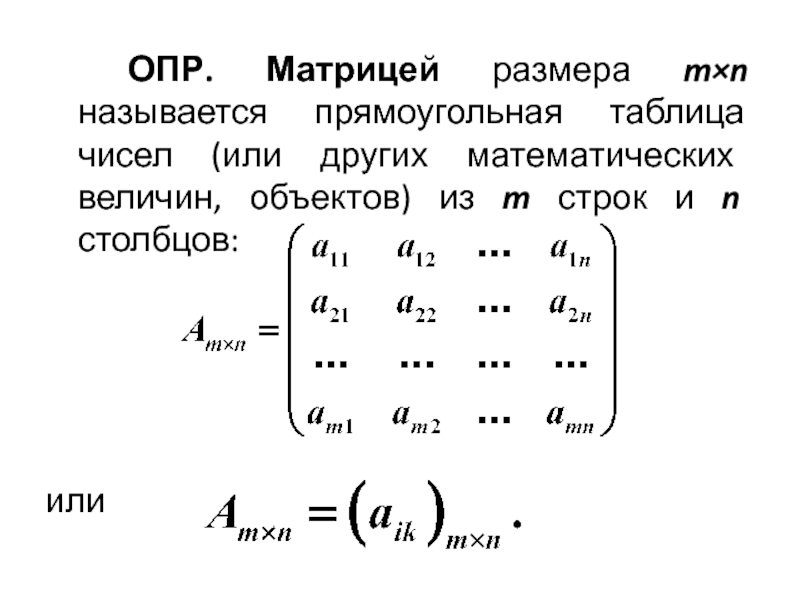
- 8. ОПР. Матрицей размера m×n называется прямоугольная таблица
- 9. Числа, образующие матрицу, называются элементами матрицы: –
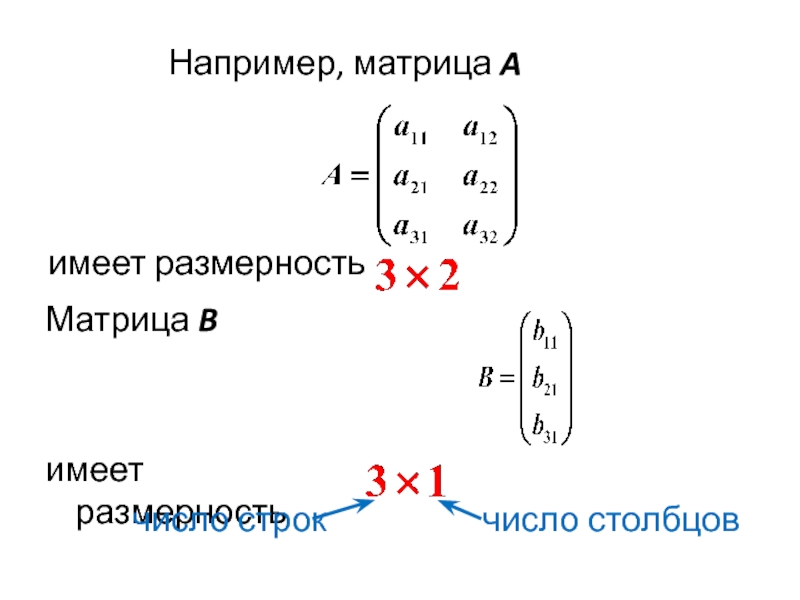
- 10. Например, матрица A имеет
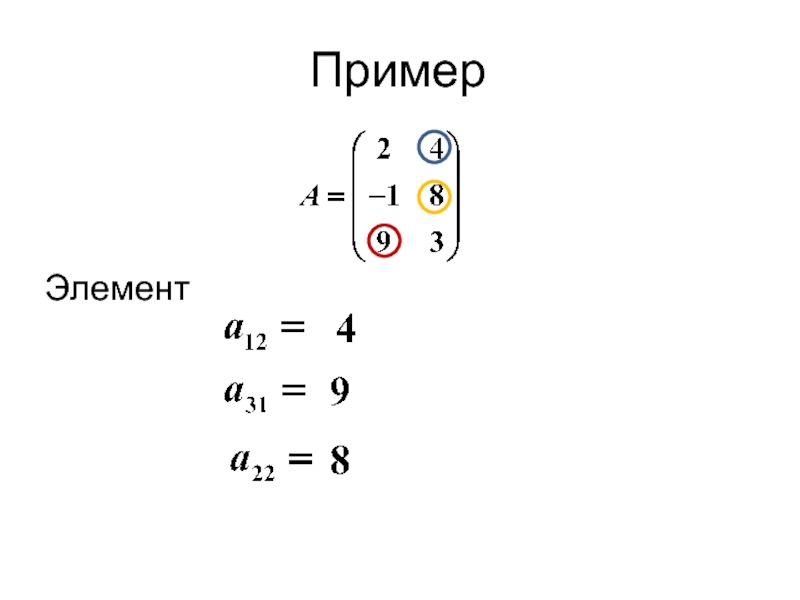
- 11. Пример Элемент
- 12. ОПР. Матрицы A и B одинаковых размеров
- 13. Пример Дано:
- 14. ОПР. Квадратной матрицей n-го порядка называется матрица
- 15. Матрица размерности m×1 называется матрицей-столбцом. Матрица размерности 1×n называется матрицей-строкой. Пример.
- 16. ОПР. Квадратная матрица называется диагональной, если ее
- 17. 1.2. Операции над матрицами К линейным операциям
- 18. ОПР. Суммой (разностью) двух матриц
- 19. Пример Найти A+B, A+C, B+C, если это возможно. Существует сумма B+C:
- 20. ОПР. Произведением матрицы
- 21. Пример
- 22. ОПР. Произведением
- 23. Операция умножения двух матриц определяется только для
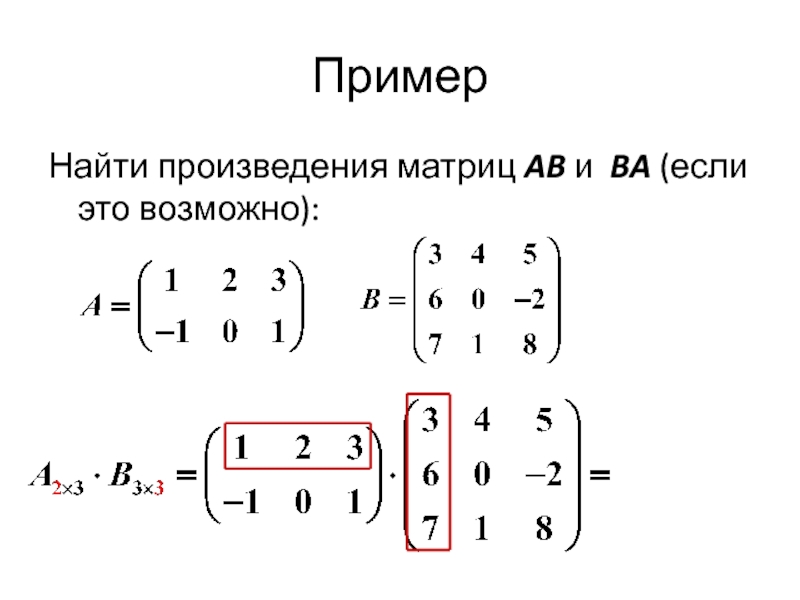
- 24. Пример Найти произведения матриц AB и BA (если это возможно):
- 25. Пример Найти произведения матриц AB и BA (если это возможно):
- 26. Произведение
- 27. ОПР. Матрица, полученная из данной заменой каждой
- 28. Свойства
- 29. Элементарные преобразования матриц Перестановка местами двух рядов
- 30. ОПР. Две матрицы A и B называются
- 31. §2. Определители Любой квадратной матрице n-го порядка
- 32. Определителем квадратной матрицы 2-го порядка
- 33. Пример Вычислить определитель 1. 2.
- 34. Определителем квадратной матрицы 3-го порядка называется число
- 35. Пример Вычислить определитель: Решение.
- 36. ОПР. Минором элемента
- 37. Пример В матрице минором элемента
- 38. §3. Обратная матрица Пусть A —
- 39. ОПР. Матрицей, присоединенной к матрице
- 40. Матрица имеет
- 41. Алгоритм вычисления обратной матрицы 1. Находим определитель
- 42. 3. Находим алгебраические дополнения элементов транспонированной матрицы
- 43. Пример Вычислить обратную матрицу для матрицы
- 44. Присоединенная матрица имеет вид: Тогда обратная матрица:
- 45. Проверка:
- 46. §4. Матричные уравнения Матричные уравнения простейшего вида
- 47. Если в уравнениях матрица
- 48. Пример Решить матричное уравнение: Решение.
- 49. Значит, обратная матрица существует, и исходное уравнение
- 50. Ранг матрицы Рассмотрим матрицу размера m×n.
- 51. ОПР. Рангом матрицы A называется наивысший порядок
Литература Дымков М.П., Конюх А.В., Майоровская С.В., Петрович В.Д., Рабцевич В.А. Высшая математика (1 семестр): Учебно-методическое пособие для подготовки к компьютерному тестированию. Мн.: БГЭУ, 2011. ─ 27 с. На сайте кафедры:
Слайд 2Литература
Дымков М.П., Конюх А.В., Майоровская С.В., Петрович В.Д., Рабцевич В.А. Высшая
математика (1 семестр): Учебно-методическое пособие для подготовки к компьютерному тестированию. Мн.: БГЭУ, 2011. ─ 27 с. На сайте кафедры: http://bseu.by/hm/uchm/test/VM1.pdf В локальной сети БГЭУ:\\Arhive\UchebM\Естественнонаучные\Высшая математика
Слайд 7 Понятие матрицы и основанный на нем раздел математики – матричная алгебра
имеют важное значение для экономистов, так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
1.1. Основные понятия
Слайд 8 ОПР. Матрицей размера m×n называется прямоугольная таблица чисел (или других математических
величин, объектов) из m строк и n столбцов:
или
Слайд 9 Числа, образующие матрицу, называются элементами матрицы: – элемент, принадлежащий i-й строке
и k-му столбцу матрицы, числа i, k называются индексами элемента.
Матрицы обозначаются A, B, C … .
Матрицы обозначаются A, B, C … .
Слайд 12 ОПР. Матрицы A и B одинаковых размеров называются равными, если равны
их соответствующие элементы:
ОПР. Матрица, у которой все элементы равны нулю, называется нулевой. Она обозначается
Слайд 14 ОПР. Квадратной матрицей n-го порядка называется матрица размера n×n. Обозначается
В квадратной матрице элементы
образуют главную диагональ.
Слайд 15 Матрица размерности m×1 называется матрицей-столбцом.
Матрица размерности 1×n называется матрицей-строкой.
Пример.
Слайд 16 ОПР. Квадратная матрица называется диагональной, если ее элементы на главной диагонали
не все равны нулю, а все остальные элементы равны нулю.
ОПР. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Обозначается
Матрица размера 1×1, состоящая из одного числа, отождествляется с этим числом:
ОПР. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Обозначается
Матрица размера 1×1, состоящая из одного числа, отождествляется с этим числом:
Слайд 171.2. Операции над матрицами
К линейным операциям над матрицами относятся сложение и
вычитание матриц, умножение матрицы на число.
Складывать и вычитать можно только матрицы одинаковых размеров.
Складывать и вычитать можно только матрицы одинаковых размеров.
Слайд 18ОПР. Суммой (разностью) двух матриц
и
называется такая матрица
что
т. е. матрица, элементы которой равны сумме (разности) соответствующих элементов матриц A и B.
называется такая матрица
что
т. е. матрица, элементы которой равны сумме (разности) соответствующих элементов матриц A и B.
Слайд 20 ОПР. Произведением матрицы на число
(или числа на матрицу A) называется матрица , для которой
т. е. матрица, полученная из данной умножением всех ее элементов на число . Обозначение
т. е. матрица, полученная из данной умножением всех ее элементов на число . Обозначение
Слайд 22 ОПР. Произведением матриц
и
называется матрица C размера такая, что
т. е. элемент i-й строки и j-гo столбца матрицы произведения равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B.
называется матрица C размера такая, что
т. е. элемент i-й строки и j-гo столбца матрицы произведения равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B.
Слайд 23 Операция умножения двух матриц определяется только для случая, когда число столбцов
первой матрицы равно числу строк второй матрицы.
Если матрицы A и B квадратные одного размера, то произведения и
всегда существуют, но не обязательно равны.
Если матрицы A и B квадратные одного размера, то произведения и
всегда существуют, но не обязательно равны.
Слайд 26
Произведение не существует, так как число столбцов матрицы B
не совпадает с числом строк матрицы A .
Слайд 27 ОПР. Матрица, полученная из данной заменой каждой ее строки столбцом с
тем же номером, называется матрицей, транспонированной относительно данной. Матрицу, транспонированную относительно матрицы A, обозначают
Например, если
Слайд 29Элементарные преобразования матриц
Перестановка местами двух рядов матрицы;
Умножение всех элементов ряда матрицы
на число, отличное от нуля;
Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Под рядом матрицы понимается строка или столбец матрицы.
Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Под рядом матрицы понимается строка или столбец матрицы.
Слайд 30 ОПР. Две матрицы A и B называются эквивалентными, если одна из
них получается из другой с помощью элементарных преобразований.
Записывают:
Записывают:
Слайд 31§2. Определители
Любой квадратной матрице n-го порядка A можно поставить в соответствие
число, которое называется определителем матрицы A, и обозначается , ,
(дельта).
Определителем 1-го порядка квадратной матрицы называется значение :
(дельта).
Определителем 1-го порядка квадратной матрицы называется значение :
Слайд 32 Определителем квадратной матрицы 2-го порядка
называется число, равное
обозначаемое символом
Слайд 36 ОПР. Минором элемента
квадратной матрицы A
n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.
ОПР. Алгебраическим дополнением
элемента квадратной матрицы
называется произведение
ОПР. Алгебраическим дополнением
элемента квадратной матрицы
называется произведение
Слайд 37Пример
В матрице
минором элемента является
минором
элемента является
Алгебраическое дополнение элемента
Слайд 38§3. Обратная матрица
Пусть A — квадратная матрица n-го порядка.
ОПР. Квадратная
матрица A называется невырожденной, если определитель detA не равен нулю:
В противном случае ( ) матрица A называется вырожденной.
В противном случае ( ) матрица A называется вырожденной.
Слайд 39 ОПР. Матрицей, присоединенной к матрице
называется матрица
где — алгебраическое дополнение элемента данной матрицы A.
Матрица называется обратной к квадратной матрице A, если выполняется условие
где E — единичная матрица того же порядка, что и матрица A.
где — алгебраическое дополнение элемента данной матрицы A.
Матрица называется обратной к квадратной матрице A, если выполняется условие
где E — единичная матрица того же порядка, что и матрица A.
Слайд 40
Матрица имеет те же размеры, что и
матрица A.
Теорема 1. Всякая невырожденная матрица имеет обратную (и причем только одну).
Теорема 1. Всякая невырожденная матрица имеет обратную (и причем только одну).
Слайд 41Алгоритм вычисления обратной матрицы
1. Находим определитель исходной матрицы.
Если
, то матрица A вырожденная и обратной матрицы не существует.
Если , то матрица невырожденная и обратная матрица существует.
2. Находим матрицу , транспонированную к матрице А.
Если , то матрица невырожденная и обратная матрица существует.
2. Находим матрицу , транспонированную к матрице А.
Слайд 42 3. Находим алгебраические дополнения элементов транспонированной матрицы и из них составляем
присоединенную матрицу
4. Вычисляем обратную матрицу по формуле:
5. Проверяем правильность вычисления обратной матрицы
4. Вычисляем обратную матрицу по формуле:
5. Проверяем правильность вычисления обратной матрицы
Слайд 43Пример
Вычислить обратную матрицу для матрицы
Решение. Найдем определитель:
Обратная матрица существует.
Слайд 46§4. Матричные уравнения
Матричные уравнения простейшего вида с неизвестной матрицей X записываются
следующим образом
В этих уравнениях A, B, X ― матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знака равенства находятся матрицы одинаковых размеров.
В этих уравнениях A, B, X ― матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знака равенства находятся матрицы одинаковых размеров.
Слайд 47 Если в уравнениях
матрица A невырожденная, то их решения записываются
следующим образом
Если то
Если то
Если то
Если то
Слайд 48Пример
Решить матричное уравнение:
Решение. Запишем данное матричное уравнение в виде
. Его решением является матрица (если существует матрица ).
Найдем обратную матрицу.
1) Найдем определитель матрицы :
Найдем обратную матрицу.
1) Найдем определитель матрицы :
Слайд 49 Значит, обратная матрица существует, и исходное уравнение имеет единственное решение.
Запишем решение
уравнения:
Слайд 50 Ранг матрицы
Рассмотрим матрицу размера m×n. Выделим в ней k строк
и k столбцов,
Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы и обозначаются
Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы и обозначаются
Слайд 51 ОПР. Рангом матрицы A называется наивысший порядок отличного от нуля минора
матрицы.
Обозначают:
Очевидно, что
Обозначают:
Очевидно, что
