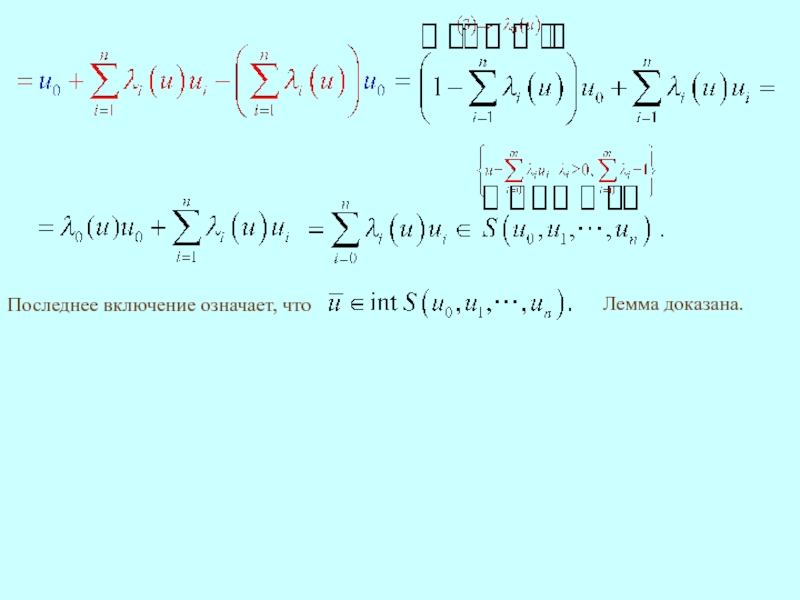- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Выпуклые множества. Лекция 8 презентация
Содержание
- 1. Выпуклый анализ. Выпуклые множества. Лекция 8
- 2. 2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
- 3. и
- 5. Покажем, что
- 6. то
- 7. Тогда
- 9. Полагаем система (2) принимает вид
- 11. Тогда находим В силу непрерывности функций вытекают неравенства
- 12. Последнее включение означает, что Лемма доказана.
- 13. Упражнение 1. линейно независимы.
- 16. Из максимальности набора линейно независимых векторов
- 17. Пример 9. Выпуклое множество представляющее
- 18. Например, множество, состоящее из
Слайд 2
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
2.6. Замыкание и внутренность выпуклых множеств(продолжение).
2.7.
Слайд 3
и
Теорема 15.
Тогда
справедливо включение
2.6. Замыкание и внутренность
имеет место
Доказательство. 1)
Слайд 7
Тогда
По доказанному первому пункту теоремы
что противоречит условию
Очевидно, что из доказанной
Теорема доказана полностью.
Упражнение 1.
Из утверждения теоремы 15
вывести утверждение теоремы 14:
внутренность выпуклых множеств выпукла.
Решение.
Слайд 8
2.7. Внутренность и относительная внутренность выпуклых множеств.
а отрезок прямой –
Лемма 1.
- симплекс, натянутый на точки
Тогда
Доказательство.
Полагаем
Покажем, что
линейных алгебраических уравнений
Слайд 14
Теорема 16.
необходимо и достаточно,
Доказательство. Необходимость.
Отсюда выводим
Необходимость доказана.
Слайд 15
Достаточность.
Обозначим через
максимальный набор линейно независимых векторов,
Обозначим через
Слайд 16Из максимальности набора линейно независимых векторов
выполняется
Теорема доказана.
По условию теоремы
Слайд 17Пример 9.
Выпуклое множество
представляющее собой единичный круг в плоскости
не
то его внутренность не пуста.
Рассмотренный пример приводит к следующему определению.
Определение 12.