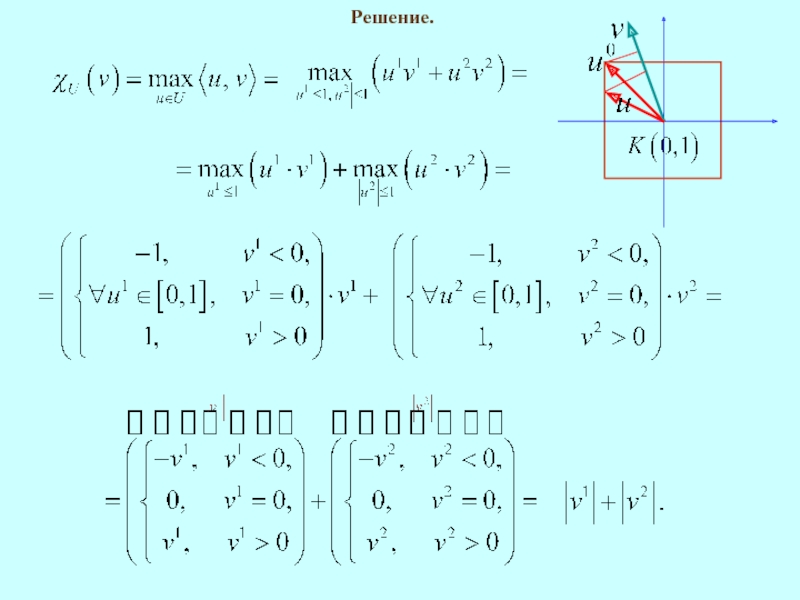- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 14 презентация
Содержание
- 1. Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 14
- 2. 4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ
- 3. 4.1. Надграфик выпуклой функции.
- 5. Упражнение. Решение.
- 6. Искомое множество строится как пересечение двух множеств
- 7. Доказательство. и определения множества Лебега выводим
- 8. Определение 3.
- 9. Дискриминант этого уравнения Покажем, что не
- 12. Теорема
- 13. Зафиксируем точку
- 14. имеем Полученное противоречие доказывает теорему.
- 15. 4.3. Опорная функция подмножества
- 16. Решение.
- 18. Свойство 4.
- 19. Пример 3.
- 20. Доказательство. Вытекает из
Слайд 2
4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И
ВЫПУКЛЫМИ МНОЖЕСТВАМИ
4.1. Надграфик выпуклой
4.2. Множество Лебега выпуклой функции.
4.3. Опорная функция подмножества пространства
4.4. Опорные функции выпуклых оболочек подмножеств
пространства
Слайд 3
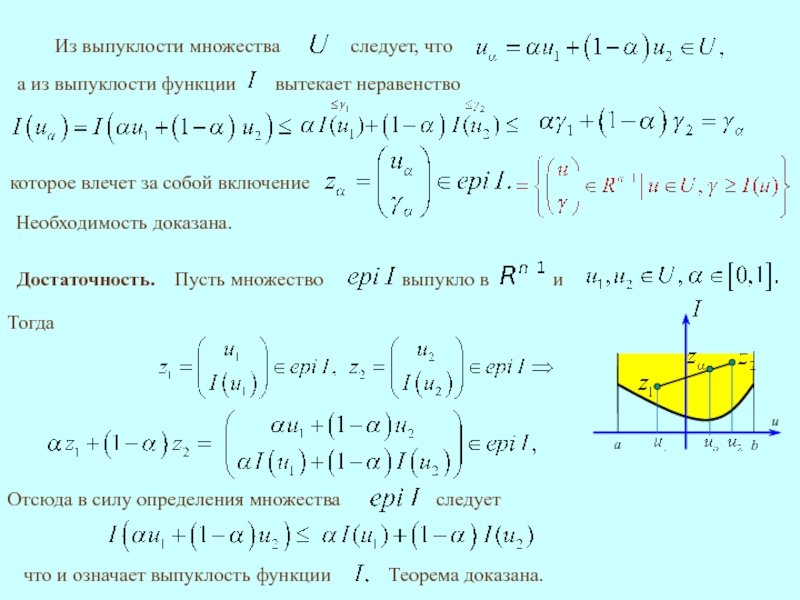
4.1. Надграфик выпуклой функции.
Определение 1.
называется множество
Теорема 1.
была выпуклой,
Доказательство.
составим их выпуклую комбинацию
Необходимость.
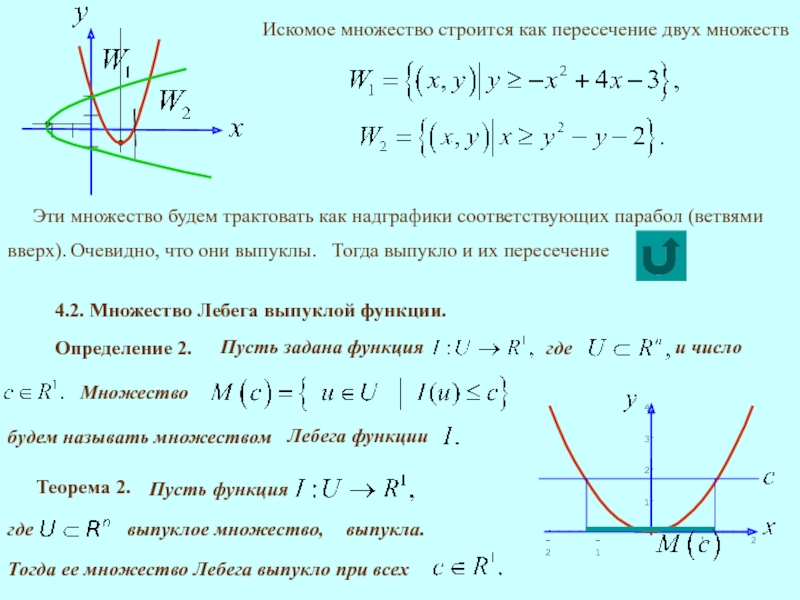
Слайд 6Искомое множество строится как пересечение двух множеств
Очевидно, что они выпуклы.
Тогда выпукло
4.2. Множество Лебега выпуклой функции.
Определение 2.
Множество
Теорема 2.
выпукла.
Слайд 7Доказательство.
и определения множества Лебега выводим
Теорема доказана.
Заметим, что обратное
не является выпуклой,
а множества Лебега для нее
Заметим, что эти множества неограниченны.
Слайд 8
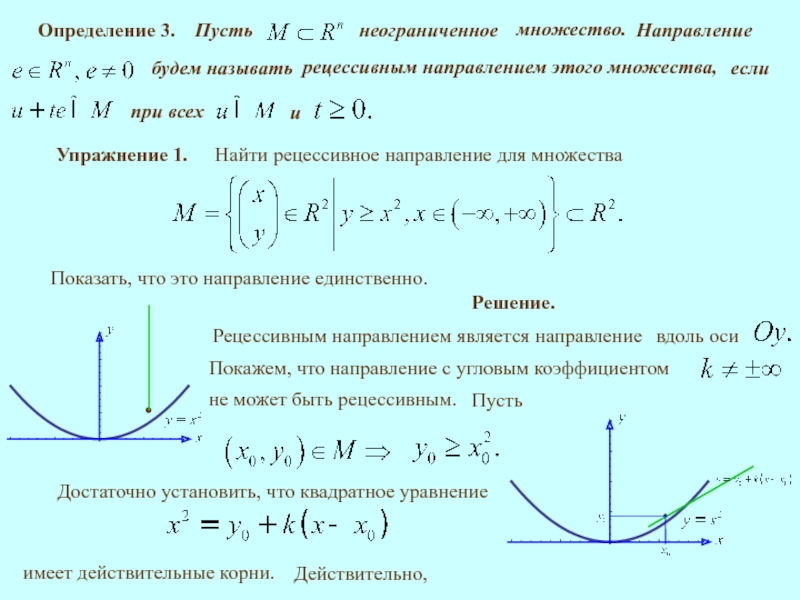
Определение 3.
Упражнение 1.
Показать, что это направление единственно.
Решение.
имеет действительные корни.
Действительно,
Слайд 9
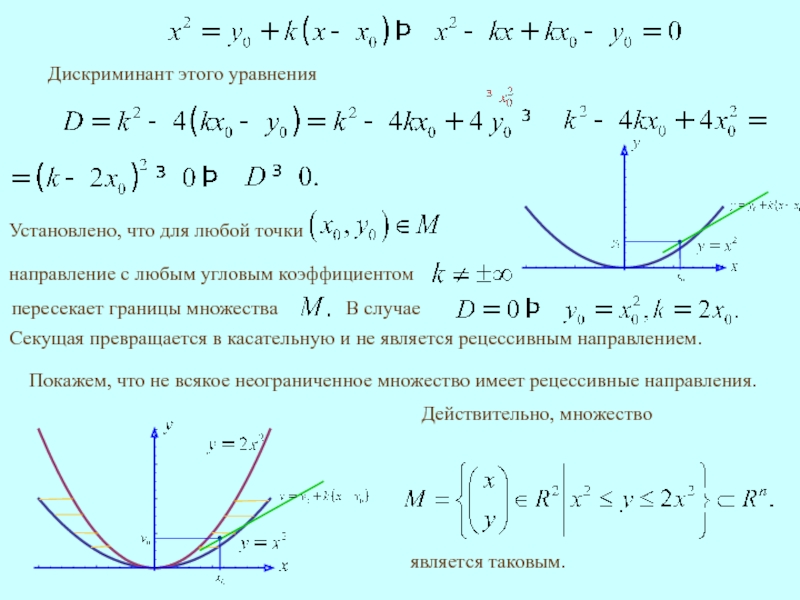
Дискриминант этого уравнения
Покажем, что не всякое неограниченное множество имеет рецессивные направления.
является
Секущая превращается в касательную и не является рецессивным направлением.
Слайд 15
4.3. Опорная функция подмножества пространства
Определение 4.
определенная формулой
Максимум в
и непрерывности скалярного произведения.
Упражнение.
Решение.
Тогда
Упражнение.
Вычислить опорную функцию квадрата
Слайд 17
Свойство 1.
Опорная функция является положительно однородной.
Доказательство.
Свойство 2.
Доказательство.
Свойство 3.
Опорная функция является выпуклой функцией.
Доказательство.
Слайд 19
Пример 3.
Решение.
В силу представления
Свойство 5.
Доказательство.
Следствие 1.
Доказательство.
Действительно,
Слайд 20
Доказательство.
Вытекает из предыдущего следствия и свойства 1.
Свойство 6.
Доказательство.
Тогда
Следствие 2.
Действительно,