- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление площади криволинейной трапеции презентация
Содержание
- 1. Вычисление площади криволинейной трапеции
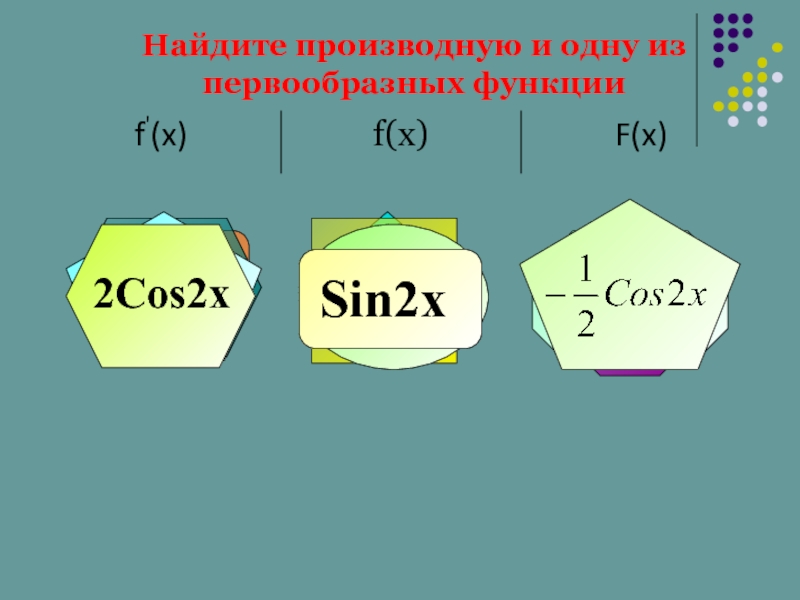
- 2. Найдите производную и одну из первообразных функции 0
- 3. Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл
- 4. Криволинейная трапеция Криволинейной трапецией называется фигура,
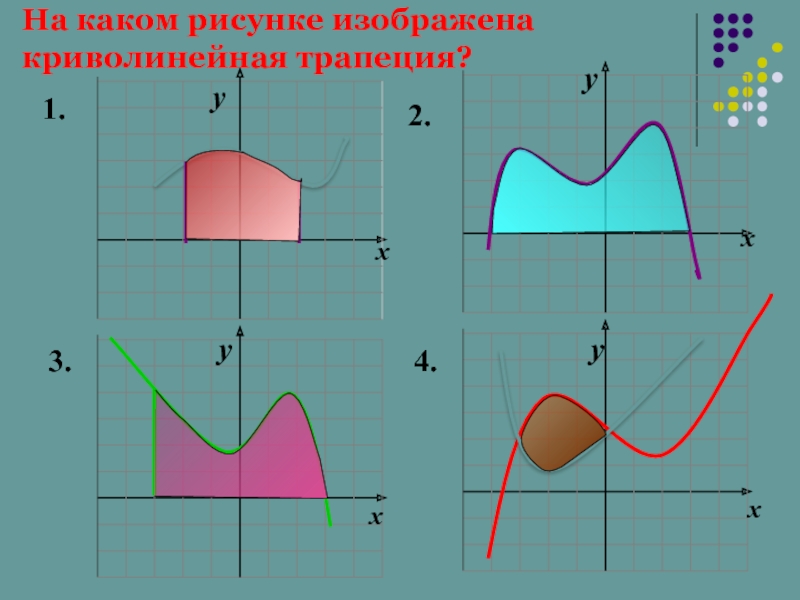
- 5. y y y y x x x
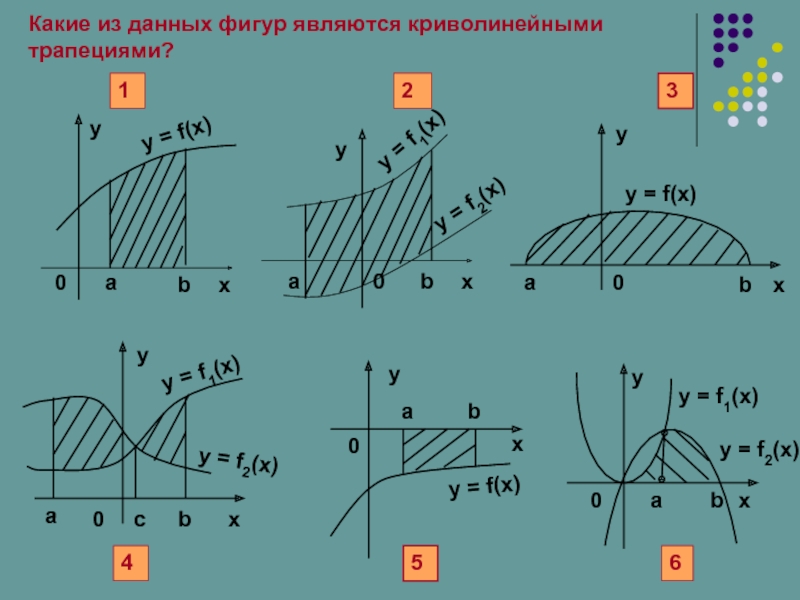
- 6. Какие из данных фигур являются криволинейными трапециями?
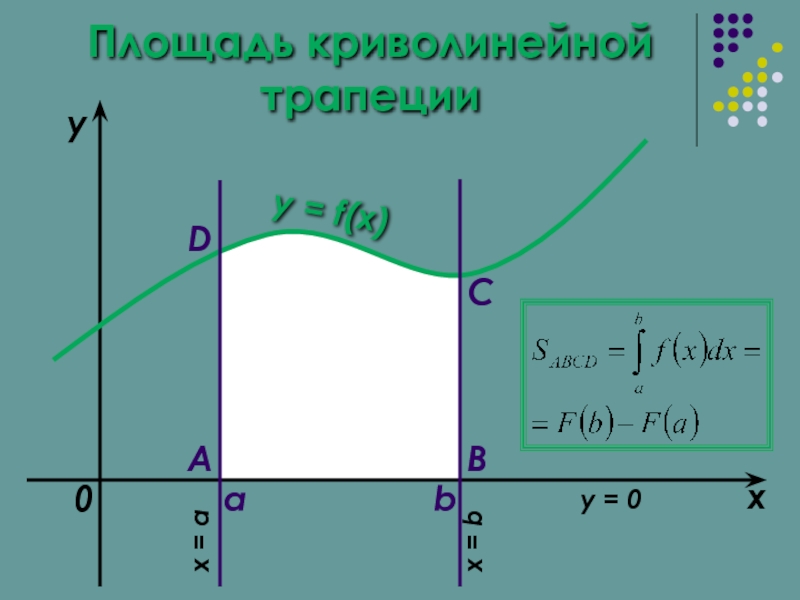
- 7. Площадь криволинейной трапеции a
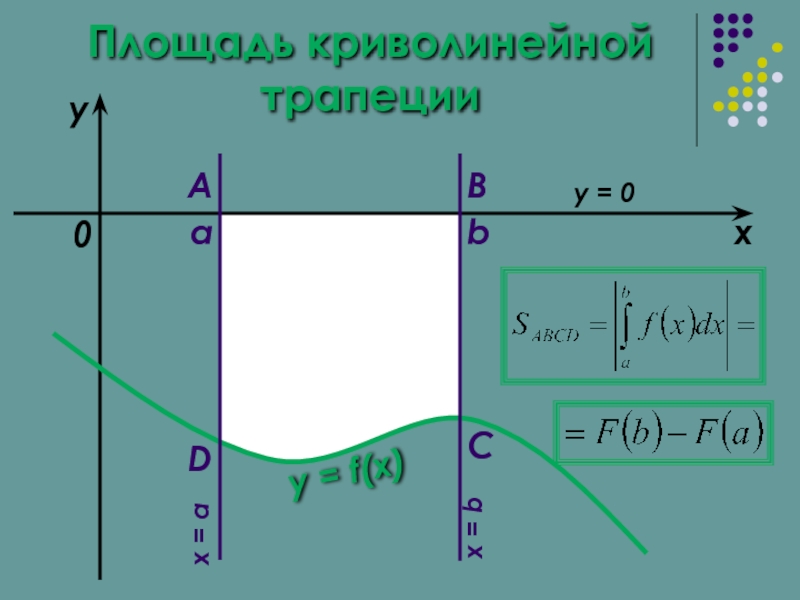
- 8. Площадь криволинейной трапеции
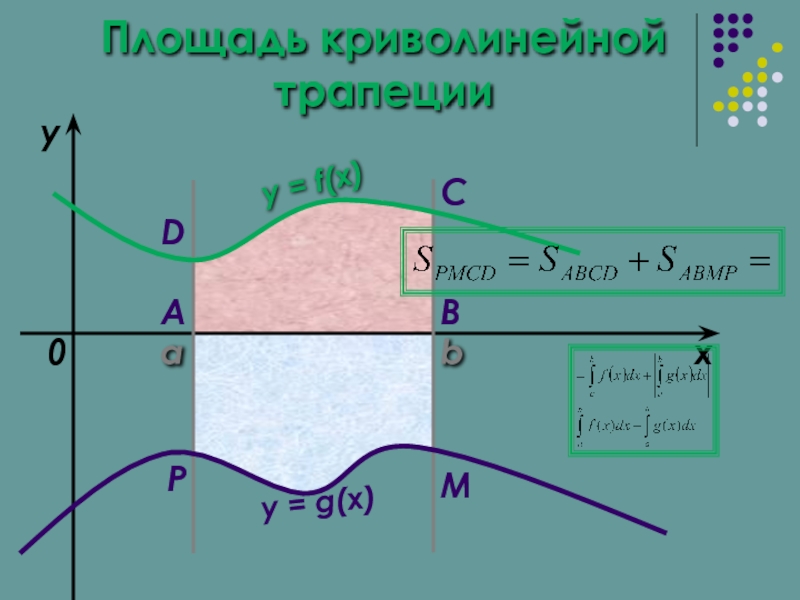
- 9. a b x y y
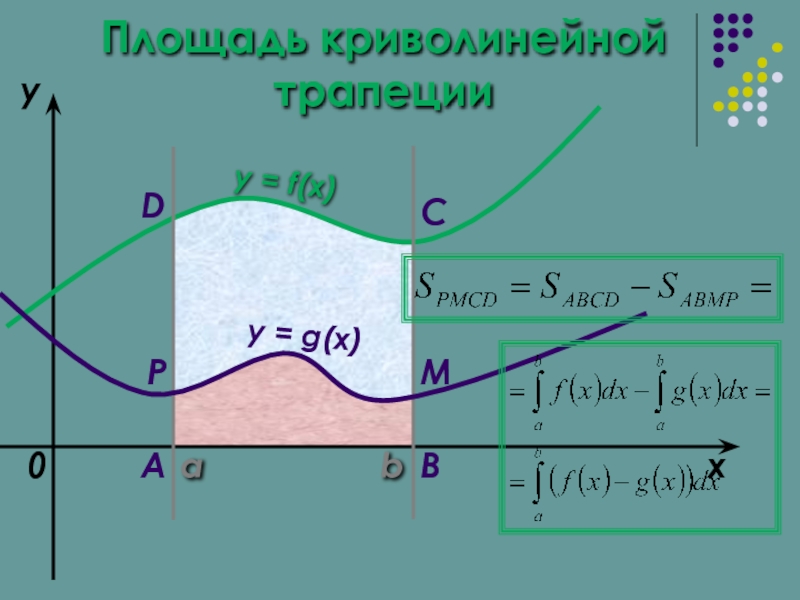
- 10. a b x
- 11. Пример 1: вычислить площадь
- 12. a b x y y
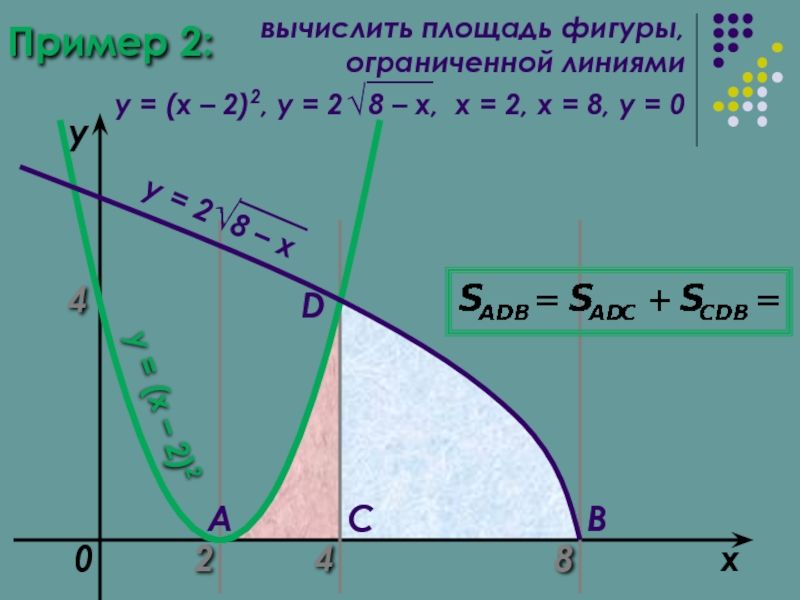
- 13. Пример 2: 2 8 x
- 14. Пример 2:
- 15. Изобразить криволинейную трапецию, ограниченную графиком
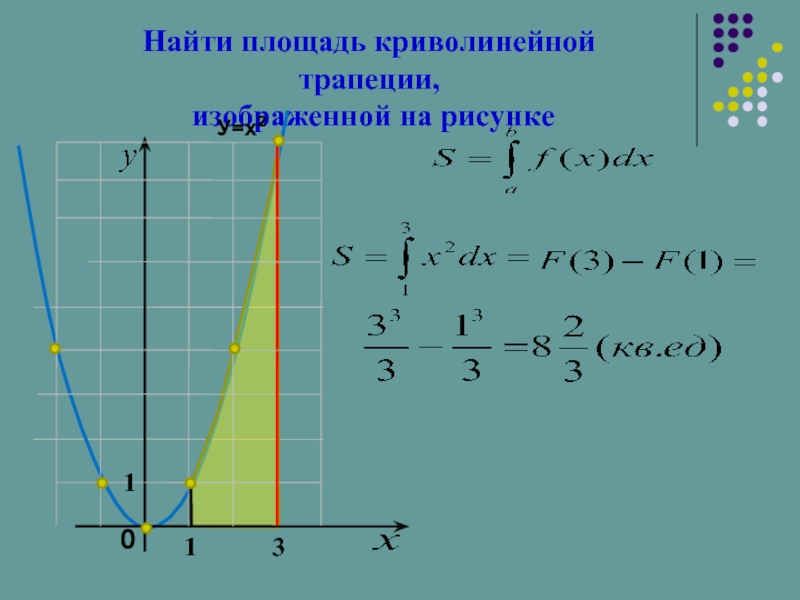
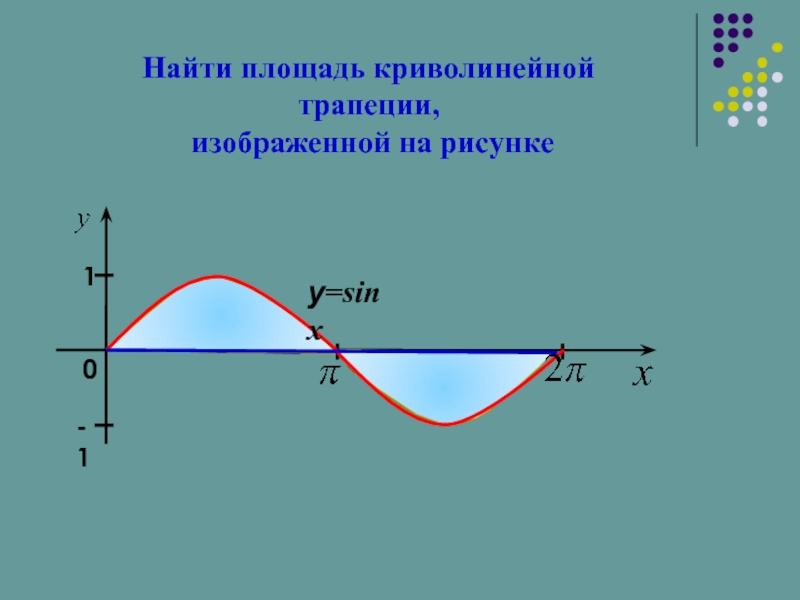
- 16. Найти площадь криволинейной трапеции, изображенной на рисунке
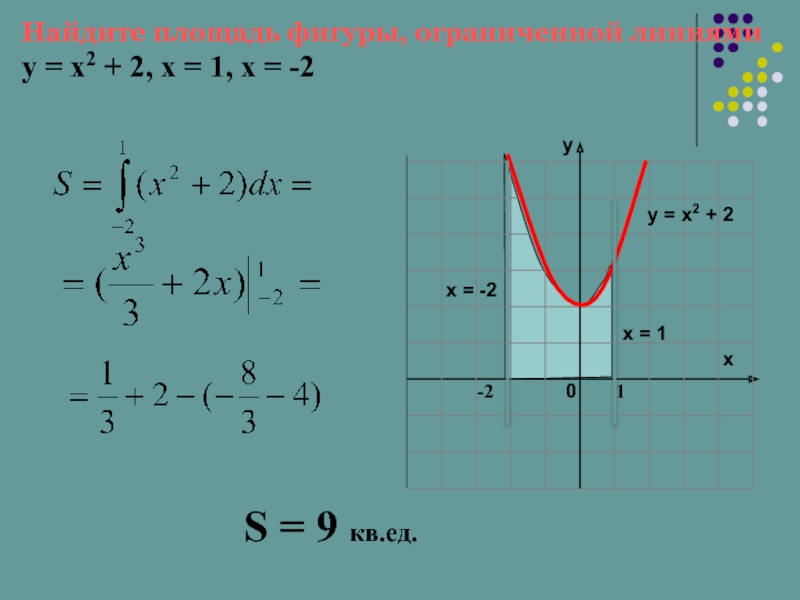
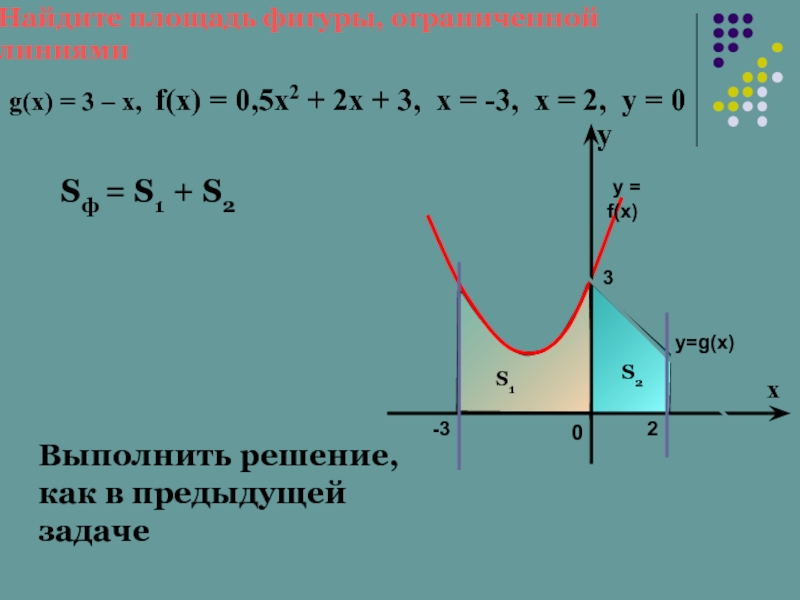
- 17. Найдите площадь фигуры, ограниченной линиями
- 18. Вычисление площадей плоских фигур Вычислить площадь фигуры,
- 19. х у = х2 - 3 Найдите
- 20. Найдите площадь фигуры, ограниченной линиями
- 21. Найти площадь криволинейной трапеции, изображенной на рисунке
- 22. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Вычисление площади криволинейной трапеции
Применение определенного интеграла для нахождения площади криволинейной трапеции.
Слайд 3Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что
ограниченной кривой у = f(x),
прямыми х = а; х = b и осью Ох, у = 0 .
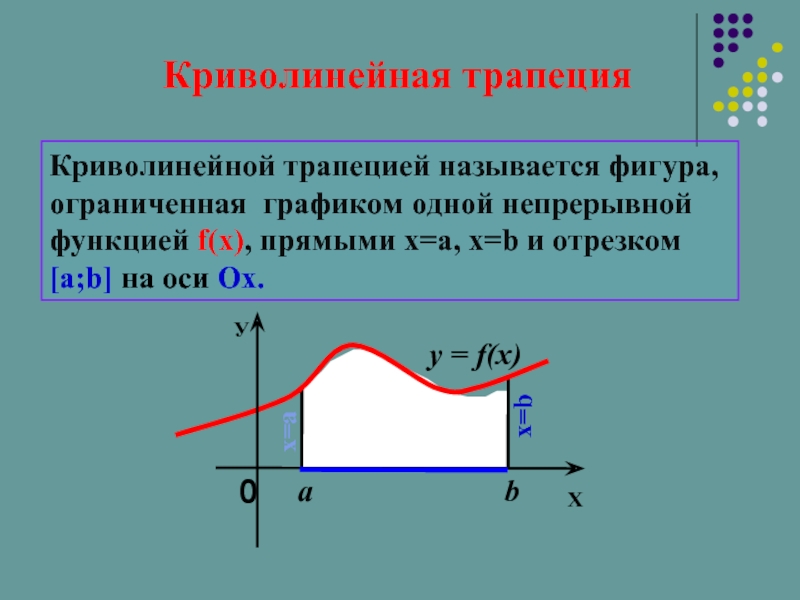
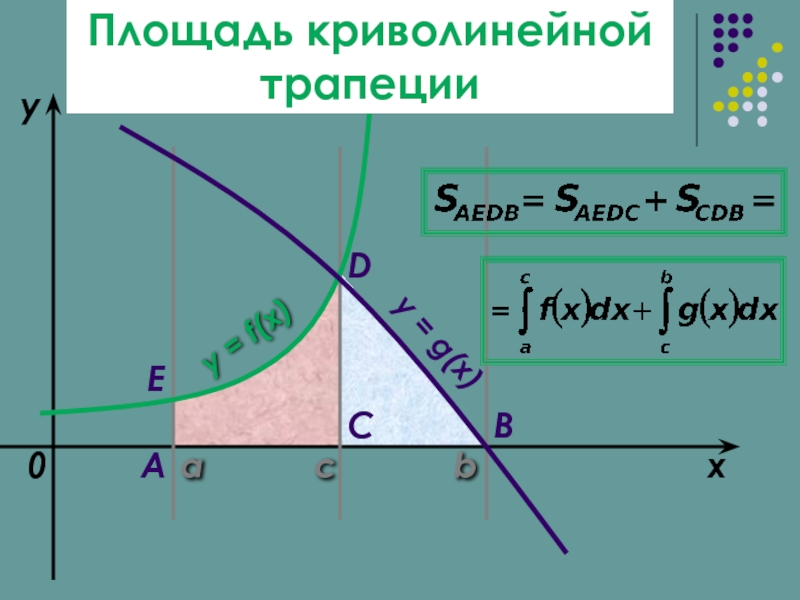
Слайд 4Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком одной непрерывной функцией f(х),
Слайд 11
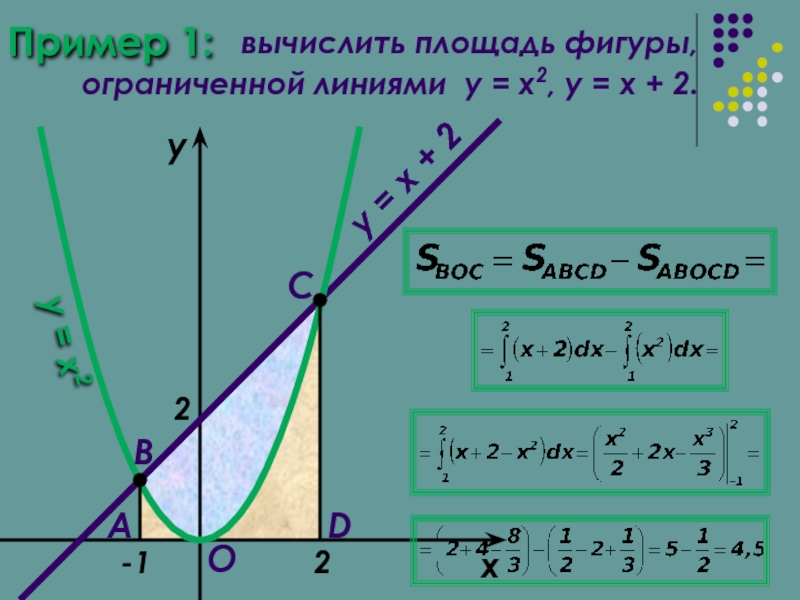
Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =
x
y
y = x2
y = x + 2
-1
2
A
B
O
D
C
2
Слайд 15
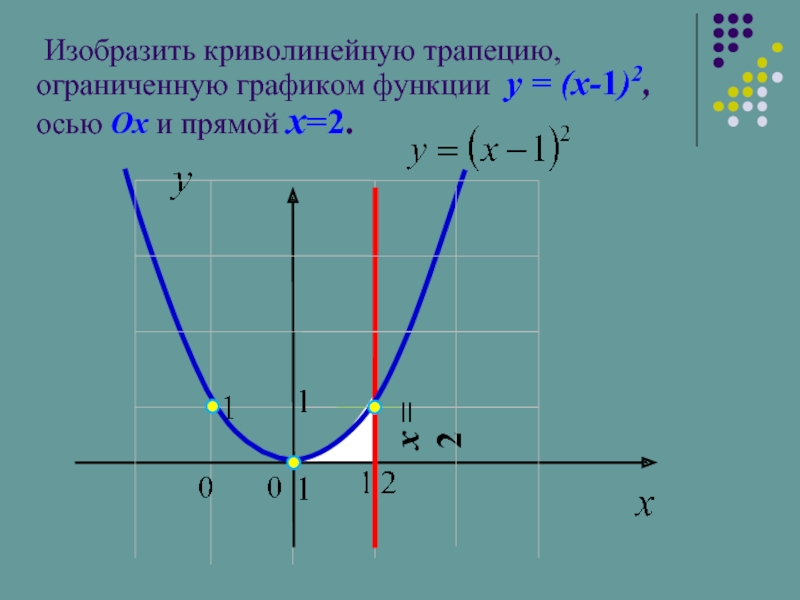
Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью
x = 2
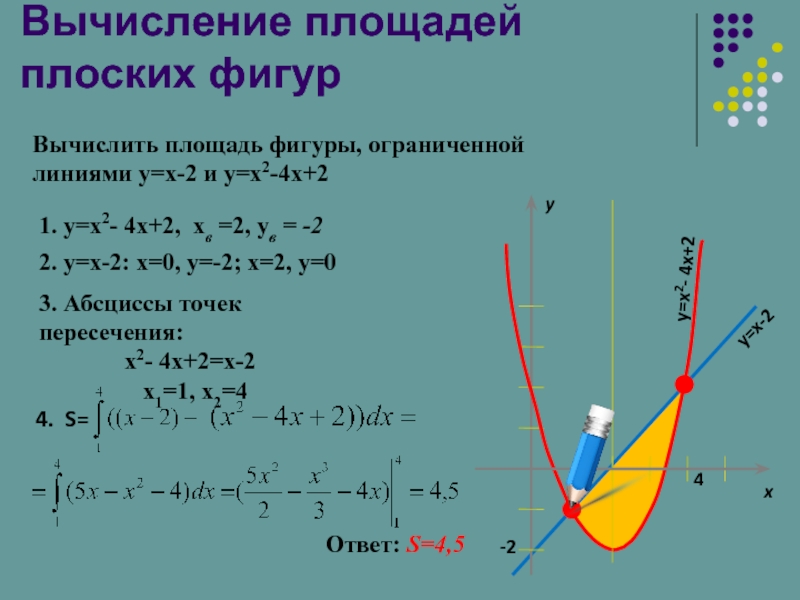
Слайд 18Вычисление площадей плоских фигур
Вычислить площадь фигуры, ограниченной
линиями y=x-2 и y=x2-4x+2
1.
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4. S=
Ответ: S=4,5
2. у=х-2: х=0, у=-2; х=2, у=0
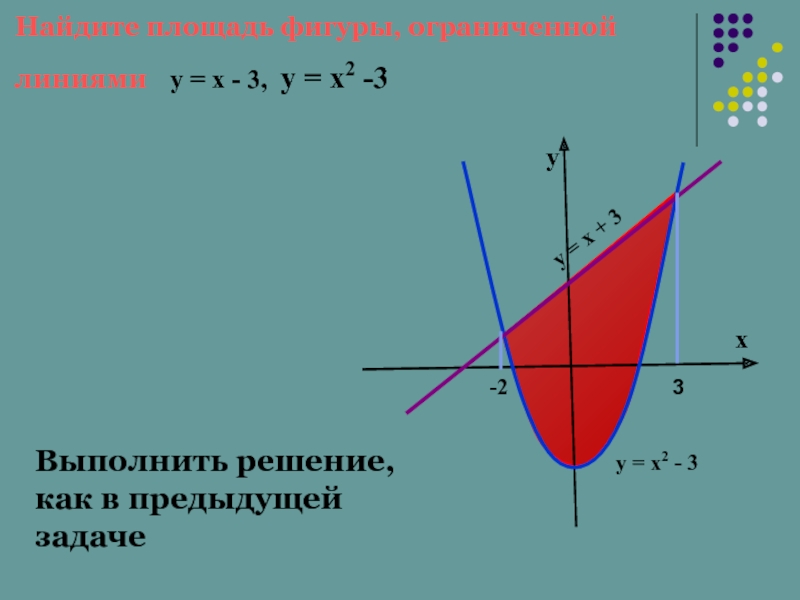
Слайд 19х
у = х2 - 3
Найдите площадь фигуры, ограниченной
линиями у
Выполнить решение, как в предыдущей задаче
Слайд 20
Найдите площадь фигуры, ограниченной линиями
g(x) = 3 – х,
у
х
S1
S2
Sф = S1 + S2
Выполнить решение, как в предыдущей задаче