- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборочное наблюдение презентация
Содержание
- 1. Выборочное наблюдение
- 2. Определение выборочного наблюдения. Сплошное
- 3. Задачи выборочного метода исследования Задачей выборочного
- 4. Ошибки выборочного наблюдения Ошибкой выборочного наблюдения, или
- 5. Основные понятия выборочного метода наблюдения Совокупность,
- 6. Чтобы различать генеральные и
- 7. Интервальная оценка параметра Х состоит в
- 8. В зависимости от метода отбора используют разные
- 9. При повторном отборе отобранная единица после обследования
- 10. Значения коэффициента доверия t рассчитаны для
- 11. При различных способах отбора единиц генеральной
- 12. Виды выборок Различают следующие виды выборок:
- 13. Серийную. выборку, в которую случайным методом
- 14. Коэффициенты доверия (t) для расчета предельных ошибок
- 15. Задача Проведено выборочное повторное
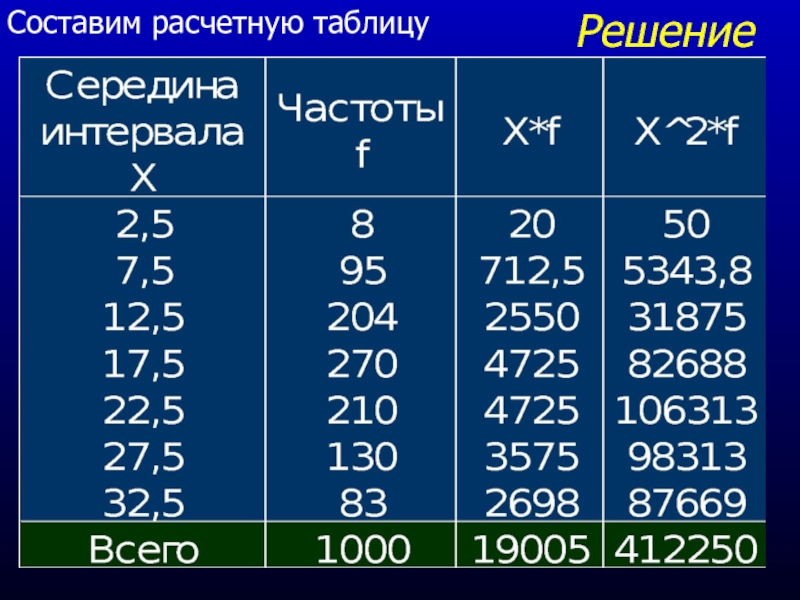
- 16. Решение Составим расчетную таблицу
- 17. Продолжение вычислений Вычислим дисперсию, среднее квадратическое
- 18. Результаты и выводы
- 19. Задача При обследовании выработки 1000 рабочих
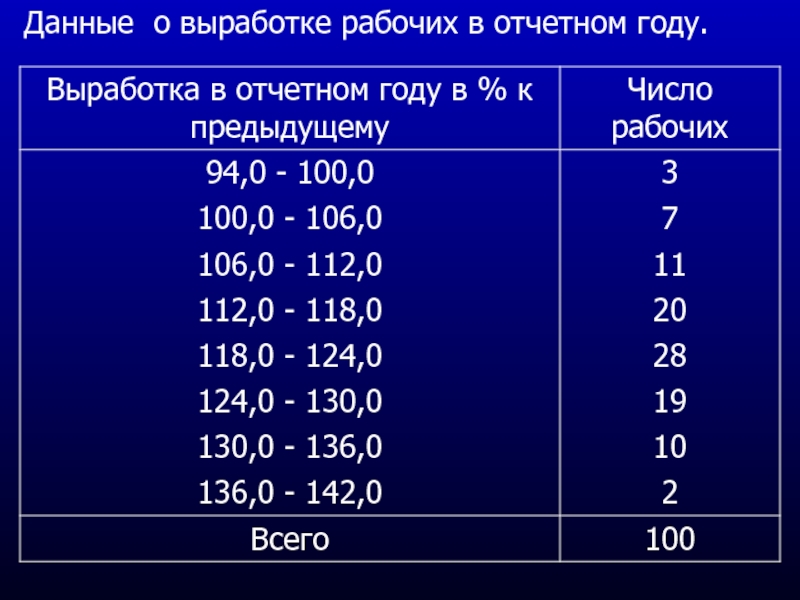
- 20. Данные о выработке рабочих в отчетном году.
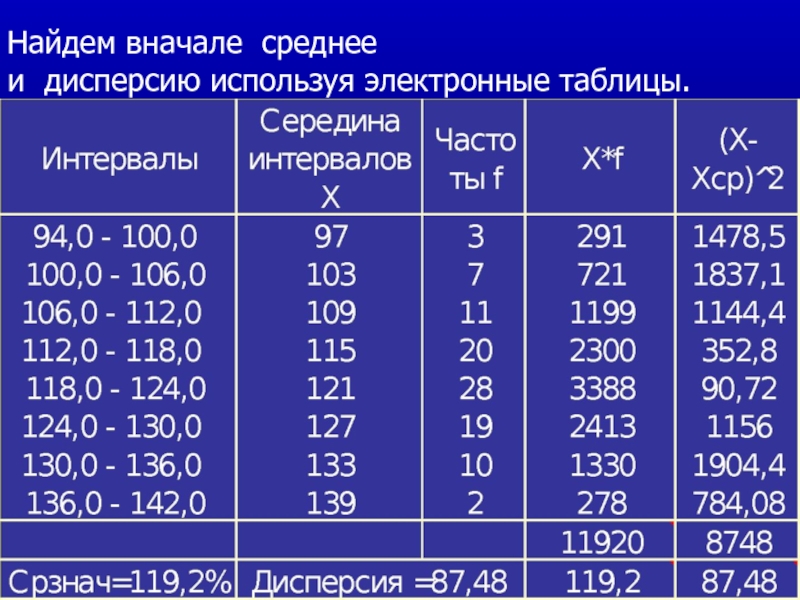
- 21. Найдем вначале среднее и дисперсию используя электронные таблицы.
- 22. Найдем среднеквадратическую ошибку выборки :
- 23. Искомую доверительную вероятность найдем из условия
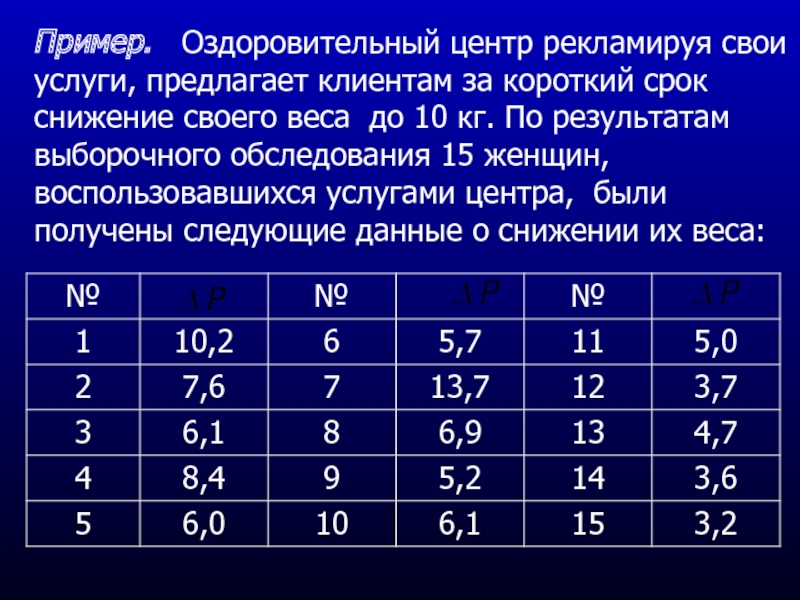
- 24. Пример. Оздоровительный центр рекламируя свои услуги,
- 25. Требуется определить на основании полученных данных
- 26. Среднюю квадратическую ошибку выборочного среднего найдем
- 27. Таким образом
- 28. Определение численности выборки Для повторных наблюдений: Для бесповторных наблюдений:
- 29. Дисперсию принимаем приближенно одним из следующих способов
- 30. Для расчета долей Дисперсия равна p*q Принимаем максимальную дисперсию = 0,25
Слайд 2Определение выборочного наблюдения.
Сплошное наблюдение предусматривает обследование всех единиц
Выборочное наблюдение - это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.
Слайд 3Задачи выборочного метода исследования
Задачей выборочного метода исследования является правильная оценка
Выяснение степени надежности найденных показателей генеральной совокупности с помощью статистических методов исследования.
Слайд 4Ошибки выборочного наблюдения
Ошибкой выборочного наблюдения, или ошибкой репрезентативности, называется разница между
Слайд 5Основные понятия выборочного метода наблюдения
Совокупность, из которой производится отбор, называется
Слайд 6 Чтобы различать генеральные и выборочные показатели, будем снабжать
Для выборочной совокупности сохраним _ _ прежнее обозначение (x, σ2)
Слайд 7 Интервальная оценка параметра Х состоит в определении границ числового интервала
Для интервальной оценки генеральной средней мы должны построить доверительный интервал с центром в точке шириной Δ.
Слайд 8В зависимости от метода отбора используют разные способы расчета среднеквадратичной ошибки.
При
При бесповторном отборе из генеральной совокупности объема N
Слайд 9При повторном отборе отобранная единица после обследования возвращается в генеральную совокупность.
При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается.
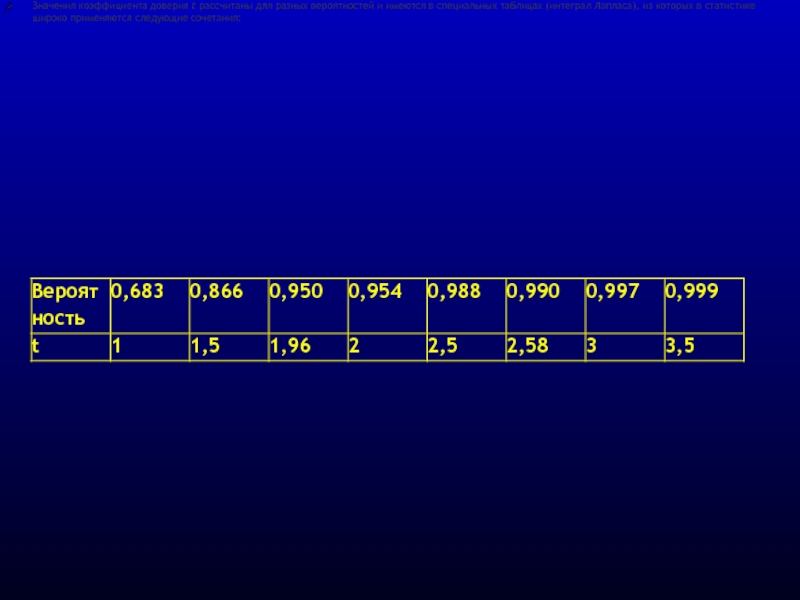
Слайд 10
Значения коэффициента доверия t рассчитаны для разных вероятностей и имеются в
Слайд 11 При различных способах отбора единиц генеральной совокупности дисперсию выборки вычисляют
При собственно-случайном и механическом отборе дисперсия выборки рассчитывается по обычной формуле.
При типическом отборе в качестве дисперсии выборки берется среднегрупповая дисперсия
При серийном отборе в качестве дисперсии выборки берется межгрупповая дисперсия. Кроме того при серийном отборе в формулах объем выборки заменяется на число серий в выборке, а объем генеральной совокупности - на число серий в генеральной совокупности (n>30, n→r, N→R)
Слайд 12Виды выборок
Различают следующие виды выборок:
Собственно–случайную выборку, образованную случайным выбором
Механическую выборку, при которой выбирается, например, каждый десятый элемент из генеральной совокупности;
Слайд 13 Серийную. выборку, в которую случайным методом отбираются не элементы, а
Типическую выборку, при которой случайным образом отбираются элементы из типических групп, на которые предварительно делится генеральная совокупность по некоторым признакам;
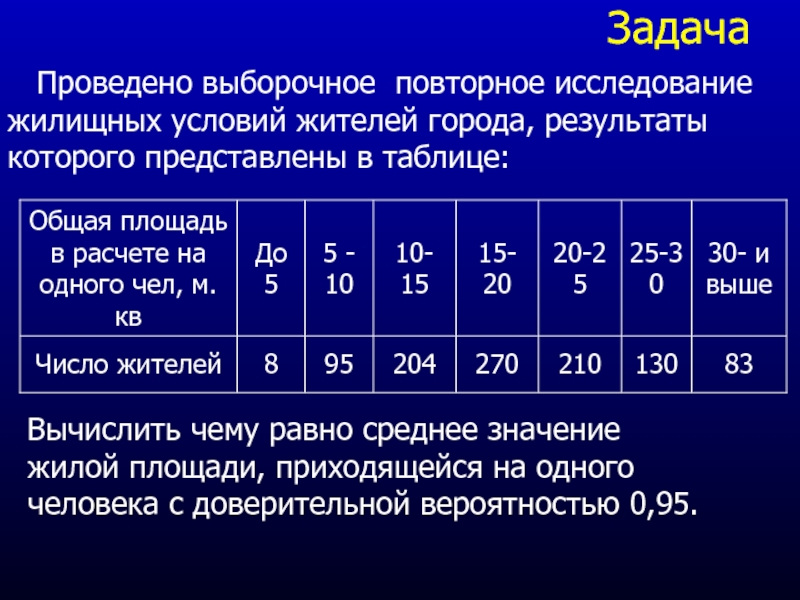
Слайд 15 Задача
Проведено выборочное повторное исследование жилищных условий жителей города,
Вычислить чему равно среднее значение жилой площади, приходящейся на одного человека с доверительной вероятностью 0,95.
Слайд 17Продолжение вычислений
Вычислим дисперсию, среднее квадратическое отклонение, среднее значение и интервал,
Слайд 19Задача
При обследовании выработки 1000 рабочих цеха в отчетном году по
Определить:
а) вероятность того, что средняя выработка рабочих цеха отличается от средней выборочной не более чем на 1%;
б) границы в которых с вероятностью 0,954 заключена средняя выработка рабочих цеха.
Слайд 23 Искомую доверительную вероятность найдем из условия (
Таким образом, вероятность того, что выборочная средняя отличается от генеральной не более чем на 1% равна 0, 71. Можно сказать, что в 71 случаях из 100 произведенное выборочное исследование даст ошибку определения средней производительности труда для всего цеха не более чем 1%.
Слайд 24Пример. Оздоровительный центр рекламируя свои услуги, предлагает клиентам за короткий
Слайд 25 Требуется определить на основании полученных данных степень достоверности рекламной информации.
Выборочная средняя и дисперсия равны
Слайд 26 Среднюю квадратическую ошибку выборочного среднего найдем по формуле
Оценим с
Число степеней свободы в данном случае равно 14, поэтому при уровне значимости 0,01 находим предельное значение параметра t =2,97, которое можно объяснить случайными факторами.
Слайд 27
Таким образом с вероятностью 0,99 отклонение генеральной средней
Теперь можно найти и предельную ошибку выборочной средней.
Слайд 29Дисперсию принимаем приближенно одним из следующих способов
Берется из предыдущих выборочных наблюдений;
Используется
Используется правило «трех сигм», согласно которому в средней величине укладывается примерно 3 стандартных отклонения.