- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в математический анализ. Теория пределов презентация
Содержание
- 1. Введение в математический анализ. Теория пределов
- 2. Основные разделы курса «Математика» 1 семестр Введение
- 3. Литература 1. Математика для экономистов: учебное пособие
- 4. Образовательный ресурс: http://ios.sseu.ru/public/eresmat/menedg/start.htm Учебное пособие Практикум Тесты
- 5. Лекция 1 Введение в математический анализ
- 6. Элементы теории множеств 1. Объединение множеств:
- 7. Стандартные множества N = {1, 2, 3,
- 8. Абсолютная величина (модуль) действительного числа Свойства модуля
- 9. Окрестность точки ε-окрестностью точки х0 называется
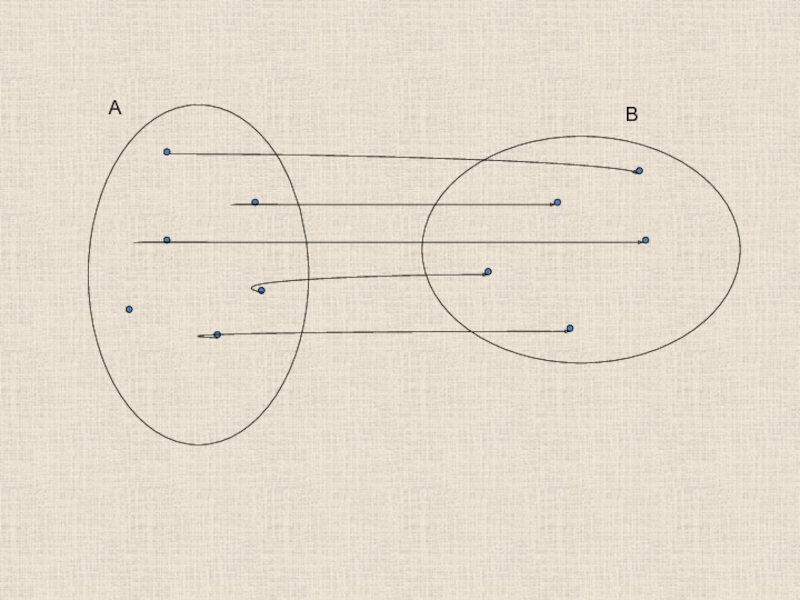
- 10. А В
- 11. А В
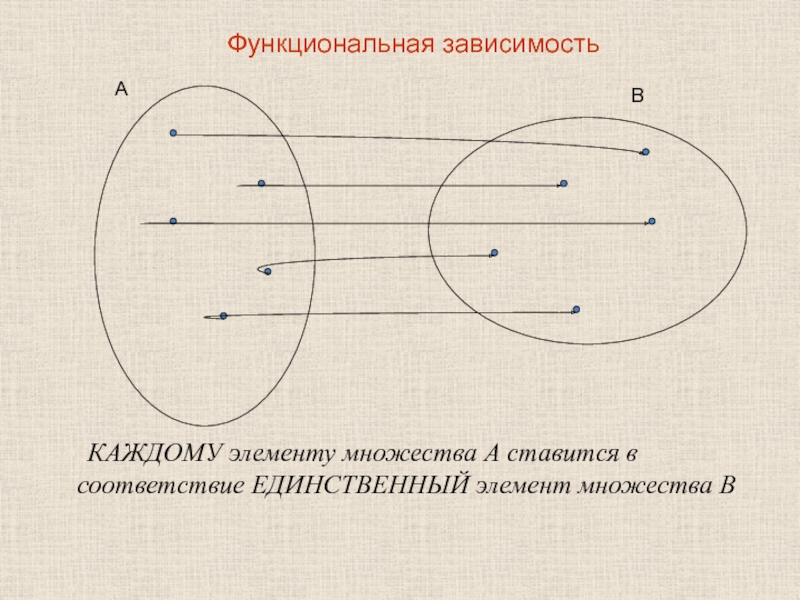
- 12. КАЖДОМУ элементу множества А ставится в соответствие
- 13. Задание функциональной зависимости между числовыми множествами X,
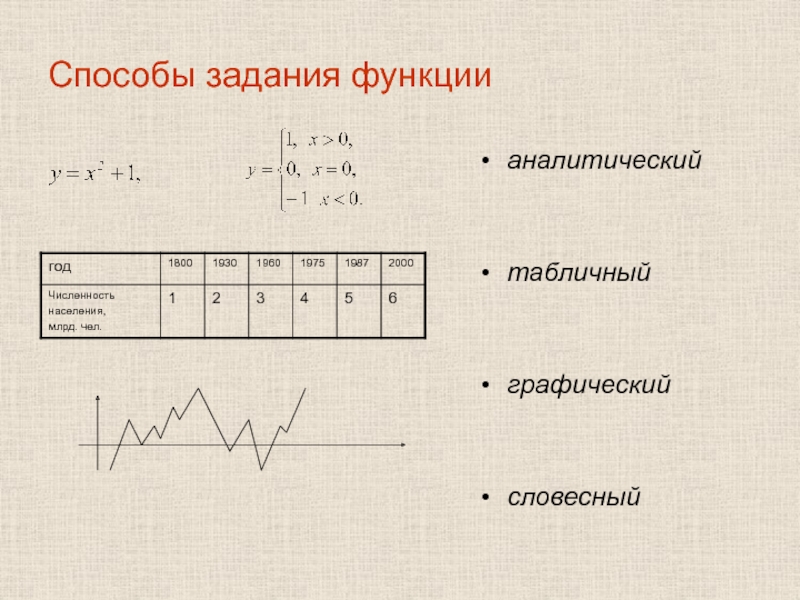
- 14. Способы задания функции аналитический табличный
- 15. Свойства функций монотонность
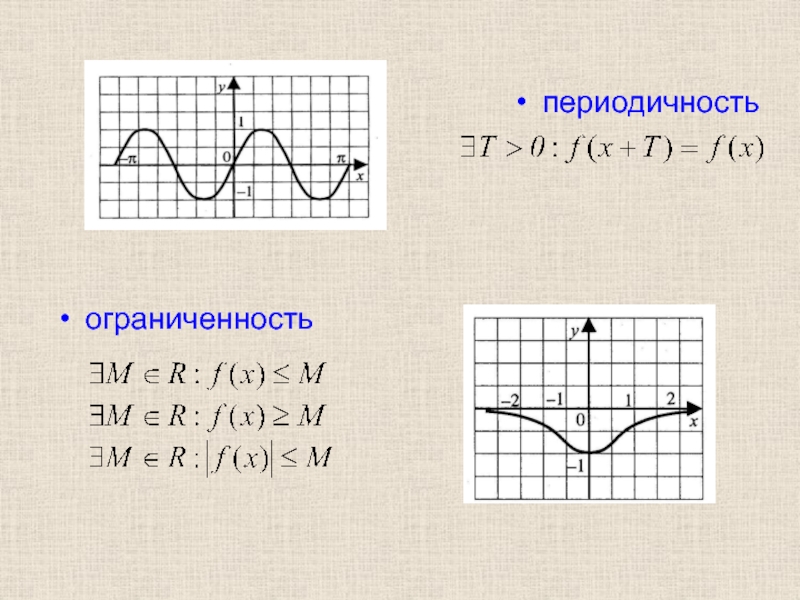
- 16. периодичность ограниченность
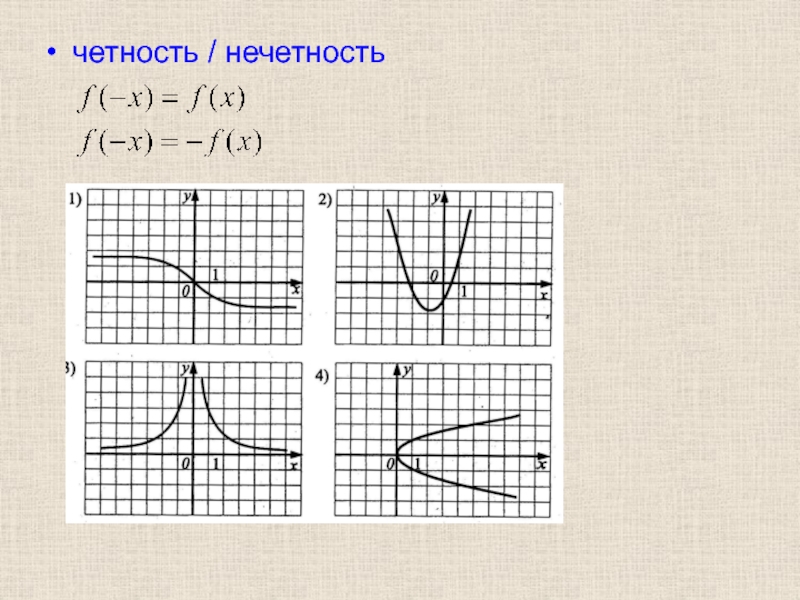
- 17. четность / нечетность
- 18. Обратная функция x y
- 19. Сложная функция
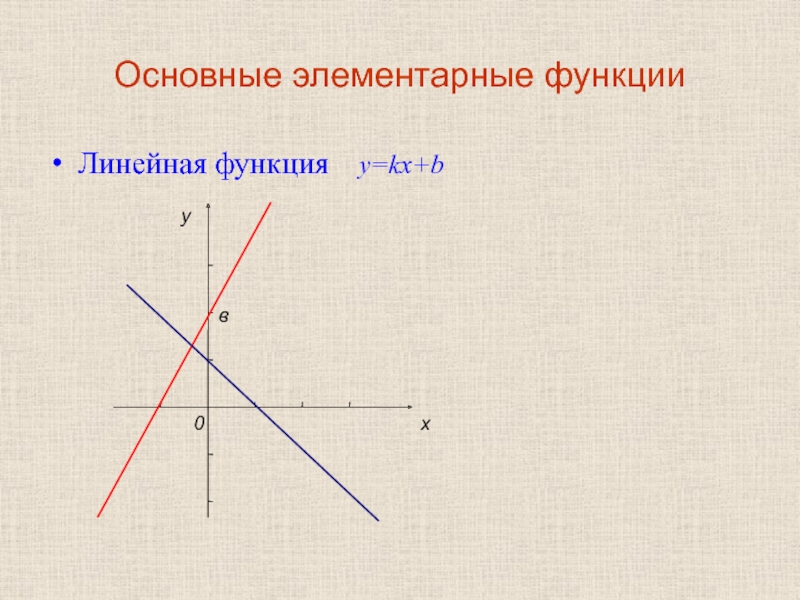
- 20. Основные элементарные функции Линейная функция y=kx+b в х у 0
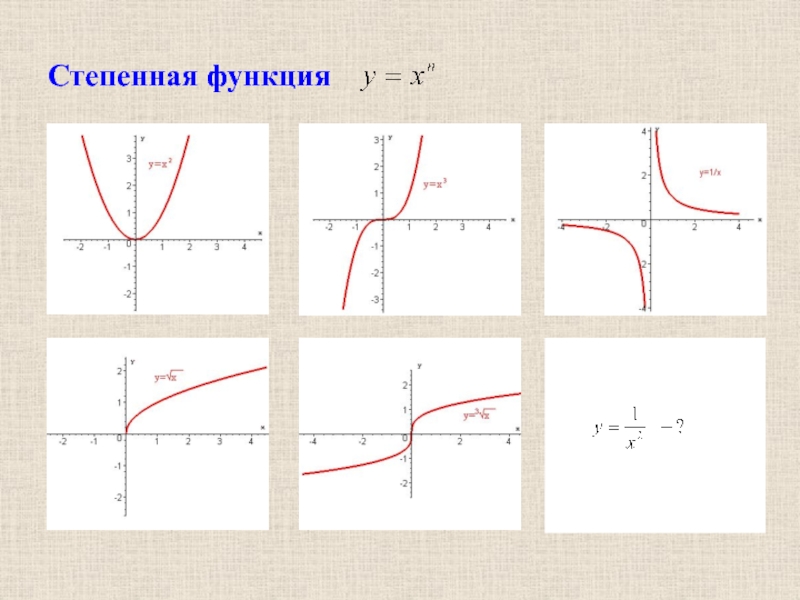
- 21. Степенная функция
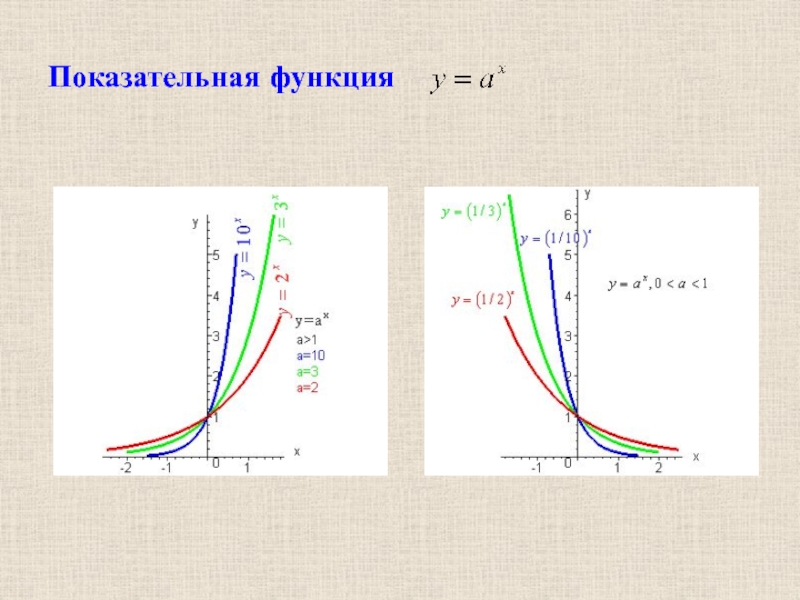
- 22. Показательная функция
- 23. Логарифмическая функция
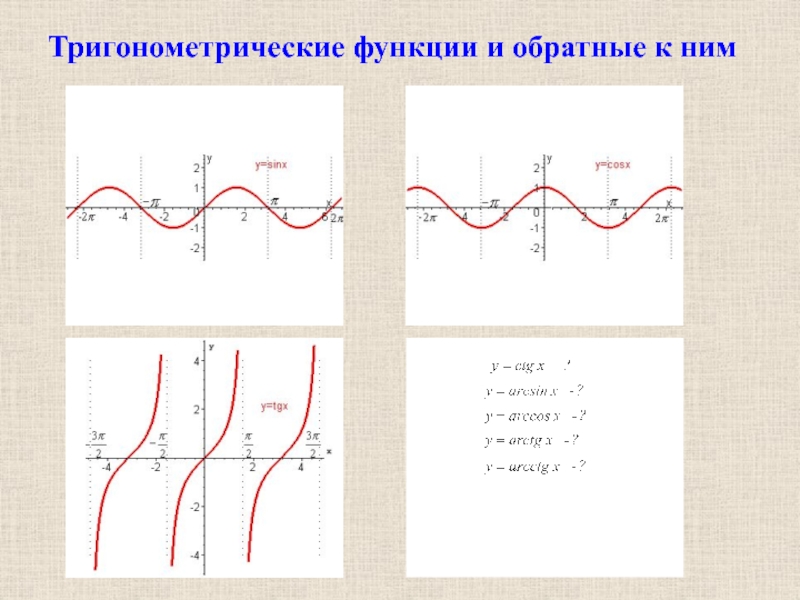
- 24. Тригонометрические функции и обратные к ним
- 25. Элементарные функции - построены из основных
- 26. Преобразования графиков функций - симметричное отображение относительно
- 27. Вопросы к семинару Модуль действительного числа. Свойства
Слайд 2Основные разделы курса «Математика»
1 семестр
Введение в математический анализ
Теория пределов
Дифференциальное исчисление
Интегральное исчисление
Функции
Слайд 3Литература
1. Математика для экономистов: учебное пособие / С.И. Макаров. – М.:
2. Высшая математика для экономистов: учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. – М.: ЮНИТИ, 2001.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: учебник: в 2-х ч.. – М.: Финансы и статистика, 2003.
Слайд 4Образовательный ресурс:
http://ios.sseu.ru/public/eresmat/menedg/start.htm
Учебное пособие
Практикум
Тесты по разделам программы
Вопросы к экзамену
Образцы решения задач
Методические пособия
Справочные
Полезная информация
Слайд 6Элементы теории множеств
1. Объединение множеств:
2. Пересечение множеств:
3. Разность множеств:
4. Дополнение множества
A
B
Слайд 7Стандартные множества
N = {1, 2, 3, …} – натуральные числа
Z =
P = { , где Z , N,- взаимно простые} – рациональные числа
(конечные или периодические десятичные дроби)
Q – иррациональные числа (бесконечные непериодические десятичные дроби)
R = { P Q } – действительные числа.
х R - собственные точки;
−∞, +∞, ∞ - несобственные точки.
Виды промежутков:
[a;b] - отрезок
(a;b) - интервал
[a;b),(a;b] - полуинтервал.
Слайд 9Окрестность точки
ε-окрестностью точки х0 называется множество точек х, удовлетворяющих условию:
х0
х0+έ
х0-έ
х
Слайд 12 КАЖДОМУ элементу множества А ставится в соответствие ЕДИНСТВЕННЫЙ элемент множества В
А
В
Функциональная
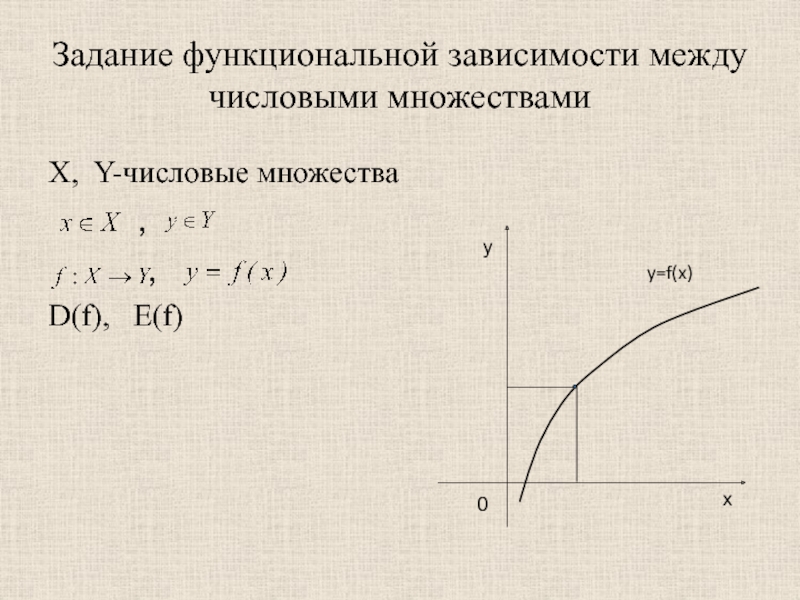
Слайд 13Задание функциональной зависимости между числовыми множествами
X, Y-числовые множества
,
D(f), E(f)
х
у
0
y=f(x)
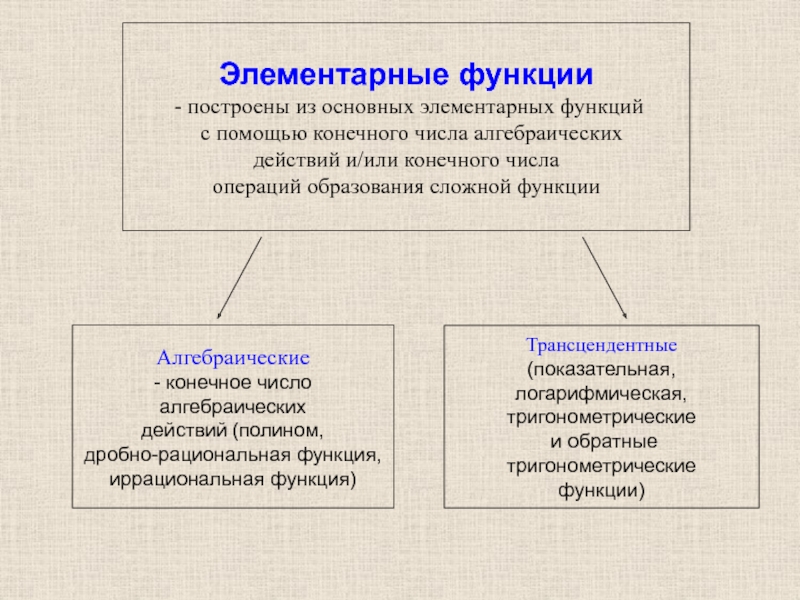
Слайд 25Элементарные функции
- построены из основных элементарных функций
с помощью конечного
действий и/или конечного числа
операций образования сложной функции
Алгебраические
- конечное число алгебраических
действий (полином,
дробно-рациональная функция,
иррациональная функция)
Трансцендентные
(показательная,
логарифмическая,
тригонометрические
и обратные тригонометрические
функции)
Слайд 26Преобразования графиков функций
- симметричное отображение относительно оси Ох.
- симметричное отображение относительно
параллельный перенос на а влево/ вправо.
параллельный перенос на а вверх/ вниз.
- растяжение (для к>1) /сжатие (для 0<к<1)
в к раз вдоль оси Оу.
растяжение (для 0<к<1) /сжатие (для к>1)
в к раз вдоль оси Ох.
часть графика, расположенная ниже оси Ох,
отображается симметрично относительно оси Ох,
остальная часть графика не изменяется.
часть графика, расположенная в правой полуплоскости
копируется в левую полуплоскость.
Слайд 27Вопросы к семинару
Модуль действительного числа. Свойства модуля. Решение неравенств вида
Окрестность точки.
Понятие функции. Область определения, область значений функции. Образ и прообраз. Способы задания функций. График функции. Явная и неявная функции. Композиция функций. Обратная функция. Свойства функций: монотонность, ограниченность, четность, периодичность.
Основные элементарные функции, их свойства и графики.
Элементарные функции, их классификация.
Преобразования графиков функций.