- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Все аксиомы и теоремы стереометрии презентация
Содержание
- 1. Все аксиомы и теоремы стереометрии
- 2. Содержание: Аксиомы стереометрии и их простейшие следствия
- 3. С1. Какова бы ни была плоскость, существуют
- 4. Простейшие следствия из аксиом стереометрии Теорема
- 5. Параллельность прямых и плоскостей Теорема 16.1:
- 6. Перпендикулярность прямых и плоскостей Теорема 17.1: Если
- 7. С1. Какова бы ни была плоскость, существуют
- 8. С2. Если две различные плоскости имеют общую
- 9. С3. Если две различные прямые имеют общую
- 10. Теорема 15.1: Через прямую и
- 11. Теорема 15.2: Если две точки прямой принадлежат
- 12. Доказательство: 1) Возьмём
- 13. Следствие из Теоремы 15.2:
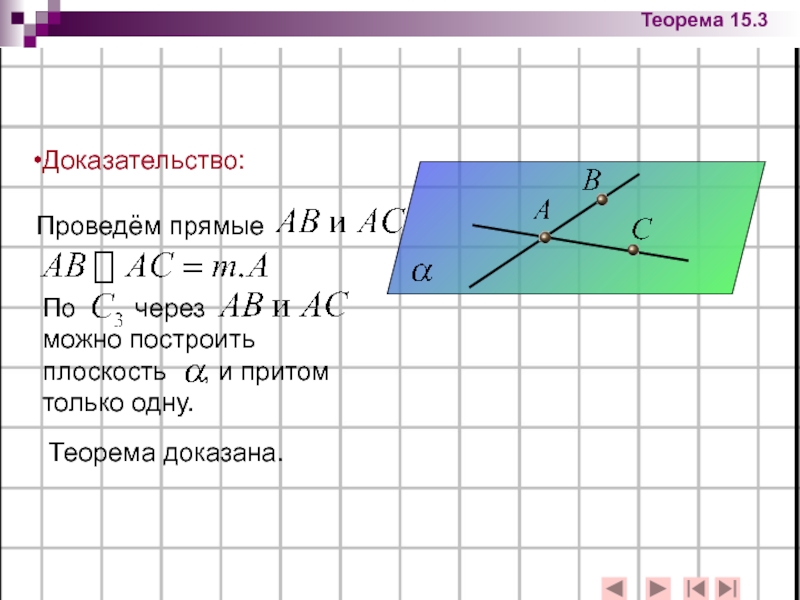
- 14. Теорема 15.3: Через три точки, не лежащие
- 15. Доказательство: Теорема доказана. Теорема 15.3
- 17. Доказательство: I) 1) Проведём плоскость
- 18. А 5) Получили, что
- 19. Признак параллельности прямых Теорема 16.2:
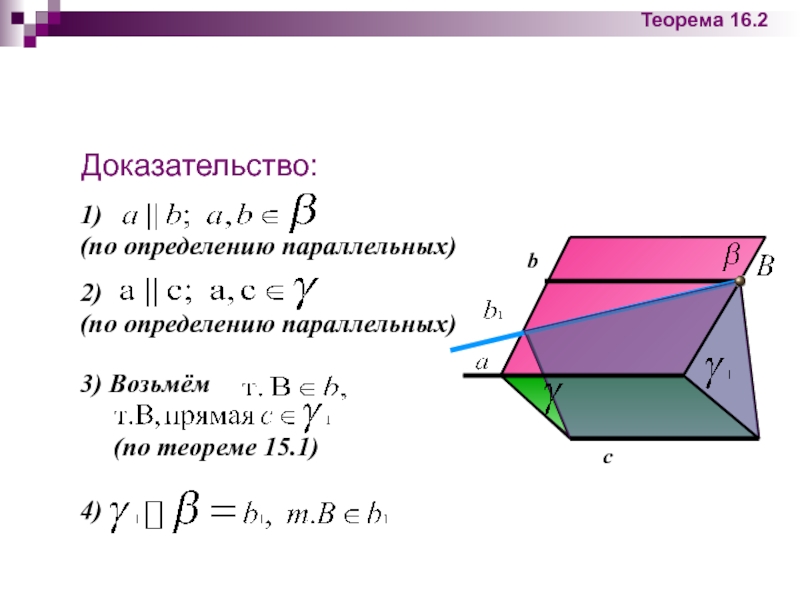
- 20. Доказательство: b c Теорема 16.2
- 21. 5) Предположим, что
- 22. Признак параллельности прямой и плоскости Дано:
- 23. 1) (по определению
- 25. Доказательство: 1) Пусть 2)
- 26. Существование плоскости, параллельной данной плоскости Теорема 16.5:
- 27. 1) Возьмём произвольные прямые 2)
- 28. Теорема 17.1: Если две пересекающиеся
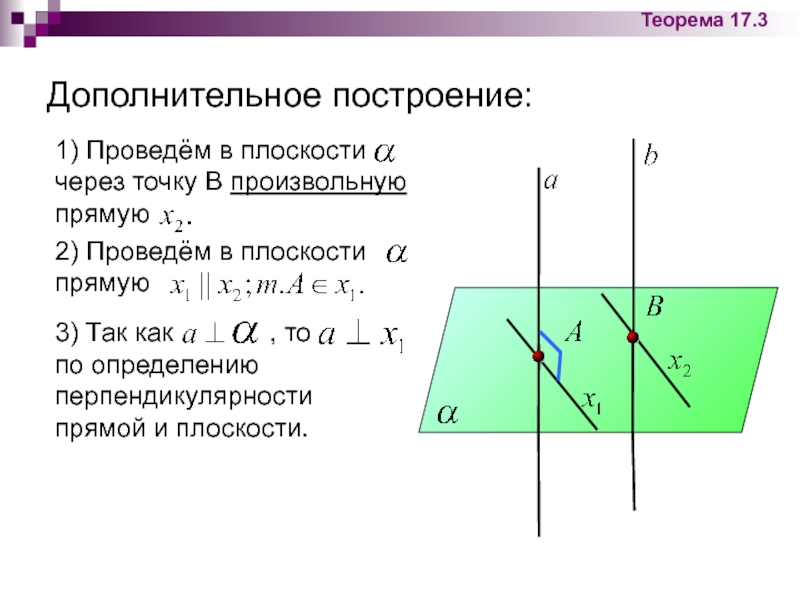
- 29. Дополнительное построение:
- 30. 4) Рассмотрим четырёхугольник
- 32. Теорема 17.2:
- 33. Дополнительное построение:
- 34. Доказательство:
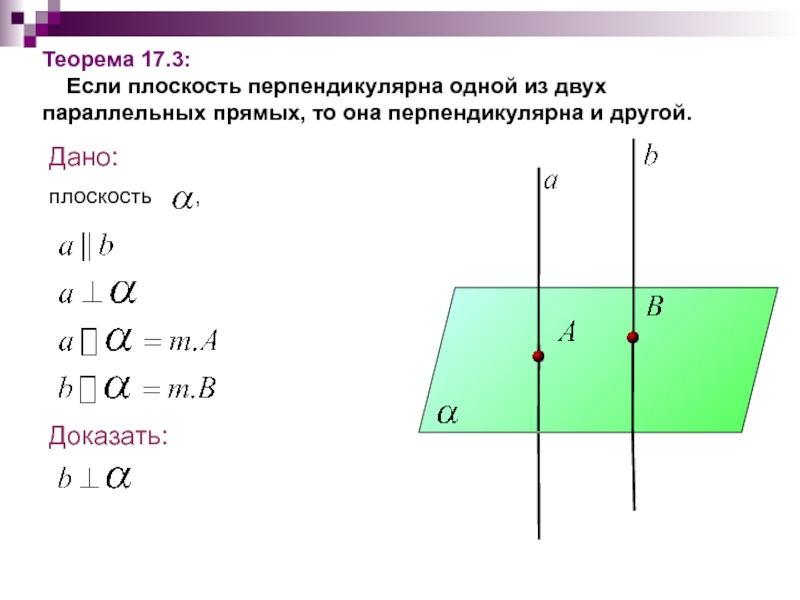
- 35. Теорема 17.3:
- 36. 2) Проведём в плоскости прямую
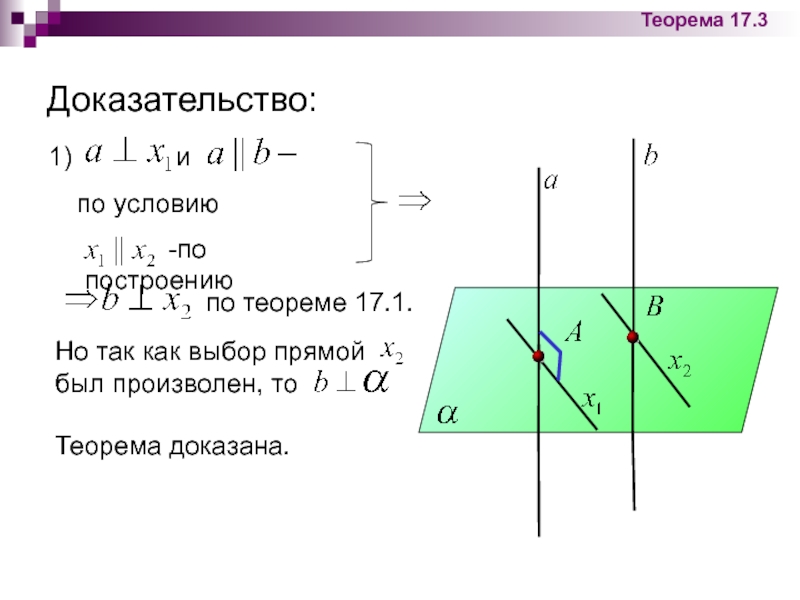
- 37. Доказательство: Теорема 17.3
- 40. Теорема 17.5: Если прямая, проведённая
- 41. Доказательство: Теорема 17.5
- 42. Теорема 17.6:
- 43. Доказательство: Теорема 17.6 1)
Слайд 2Содержание:
Аксиомы стереометрии и их простейшие следствия
Параллельность прямых и плоскостей
Перпендикулярность прямых и
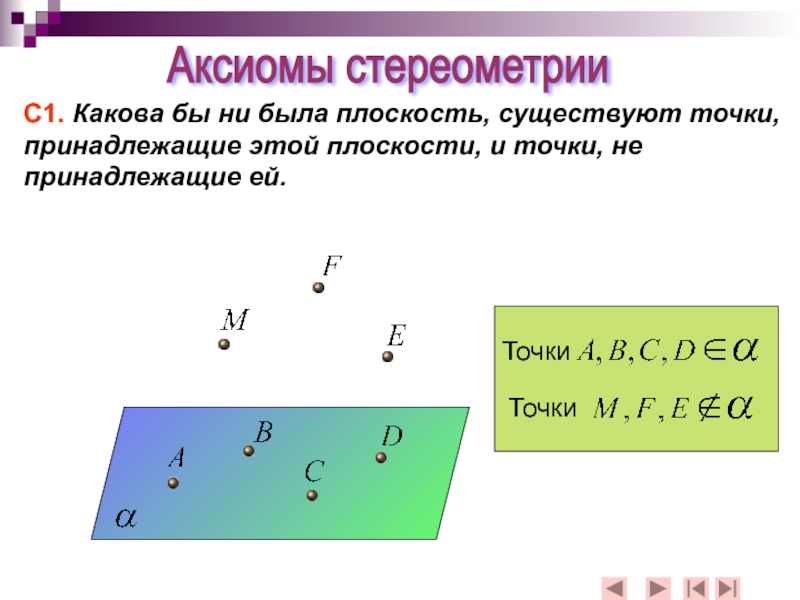
Слайд 3С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости,
Аксиомы стереометрии
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Слайд 4Простейшие следствия
из аксиом стереометрии
Теорема 15.1:
Через прямую и не лежащую
Теорема 15.2:
Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Теорема 15.3:
Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Слайд 5Параллельность прямых и плоскостей
Теорема 16.1:
Через точку вне данной прямой
Теорема 16.2:
Две прямые, параллельные третьей прямой, параллельны
Теорема 16.3:
Если прямая, не принадлежащая плоскости, параллельна какой - нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Теорема 16.4:
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Теорема 16.5:
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Слайд 6Перпендикулярность прямых и плоскостей
Теорема 17.1:
Если две пересекающиеся прямые параллельны соответственно двум
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Теорема 17.3:
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
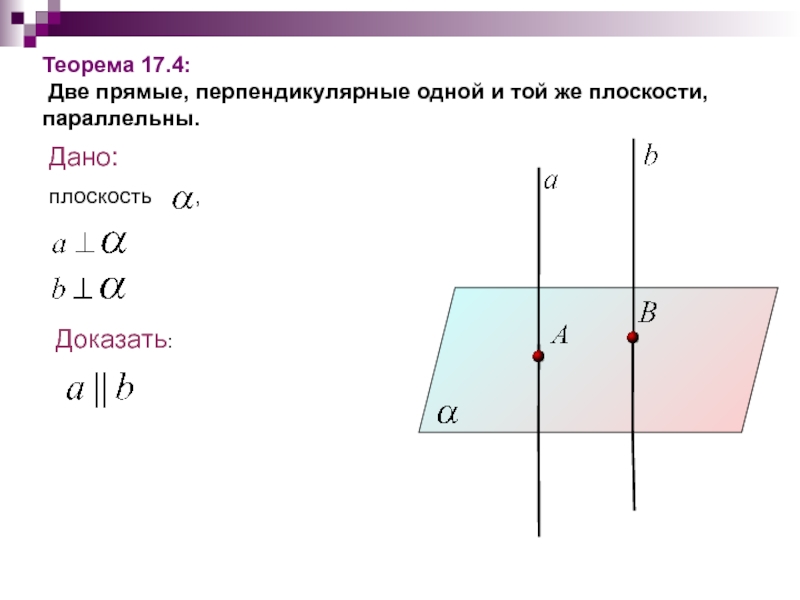
Теорема 17.4:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Теорема 17.5: Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной. Теорема 17.6: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Слайд 7С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости,
Аксиомы стереометрии
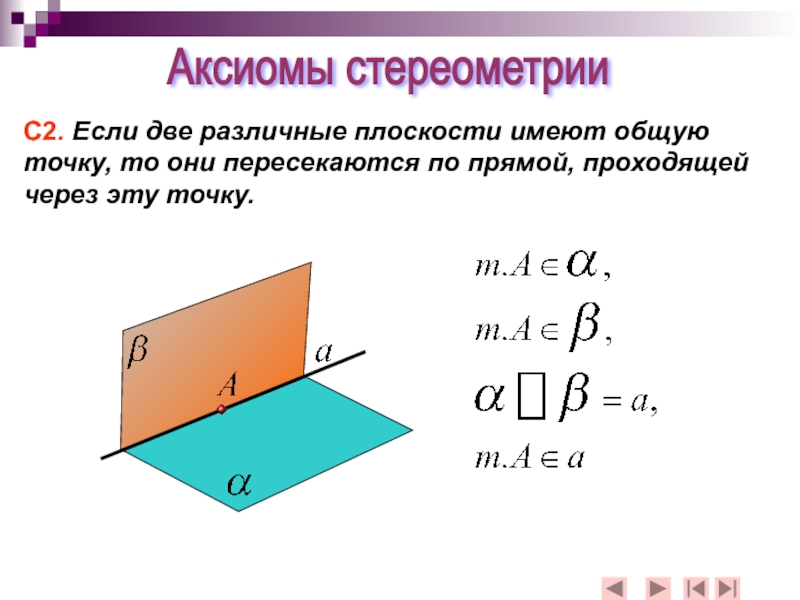
Слайд 8С2. Если две различные плоскости имеют общую точку, то они пересекаются
Аксиомы стереометрии
Слайд 9С3. Если две различные прямые имеют общую точку, то через них
Аксиомы стереометрии
Слайд 10
Теорема 15.1: Через прямую и не лежащую на ней точку можно
Дано: прямая а,
Доказать:
Доказательство:
1)Возьмём (по I)
2) Проведём прямую АВ,
3)Через прямые АВ и а проведём плоскость
- (по С3)
Теорема доказана.
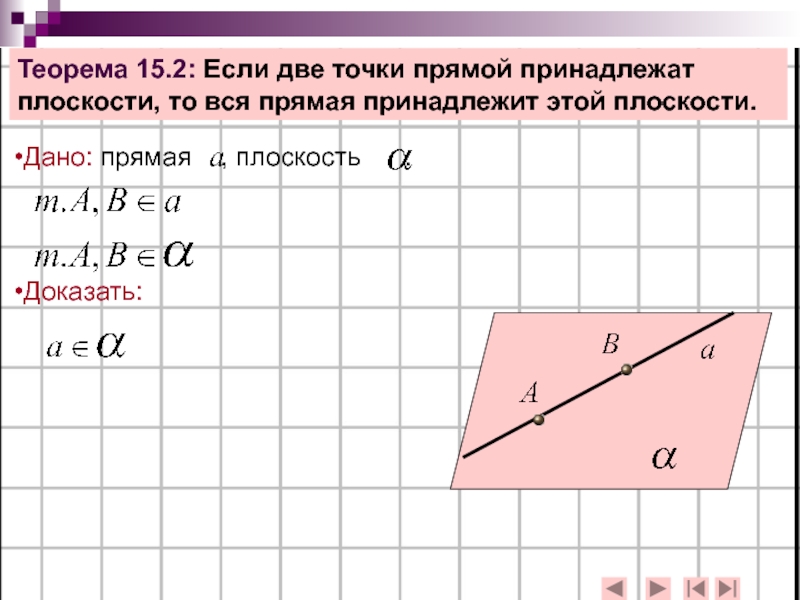
Слайд 11Теорема 15.2: Если две точки прямой принадлежат плоскости, то вся прямая
Дано: прямая , плоскость .
Доказать:
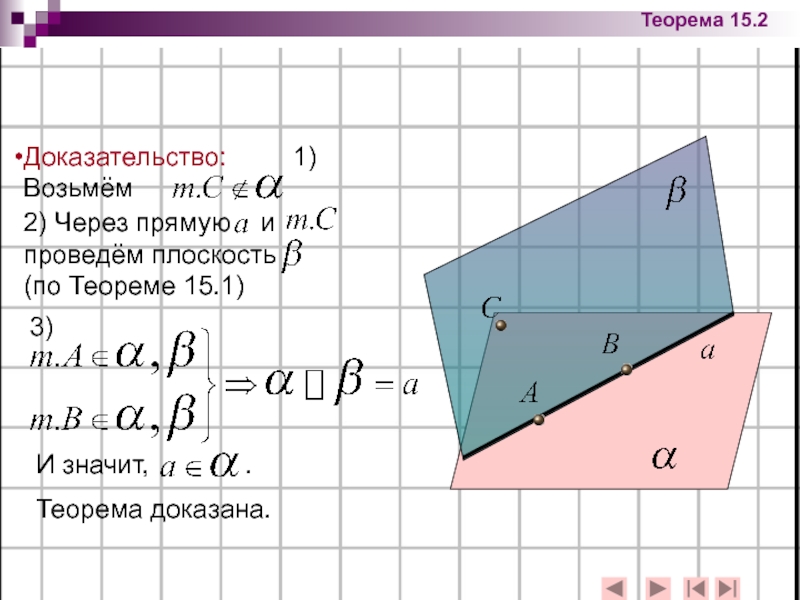
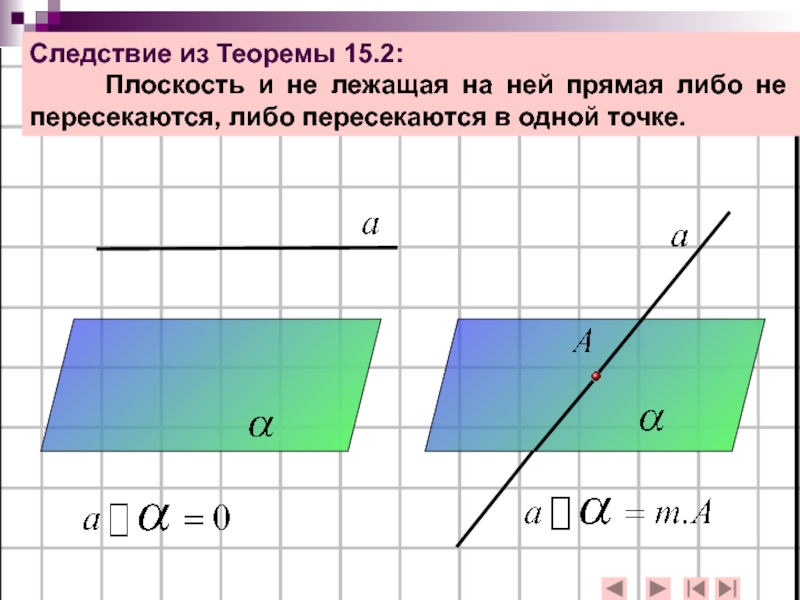
Слайд 13Следствие из Теоремы 15.2:
Плоскость и не лежащая на
Слайд 14Теорема 15.3: Через три точки, не лежащие на одной прямой, можно
Слайд 16
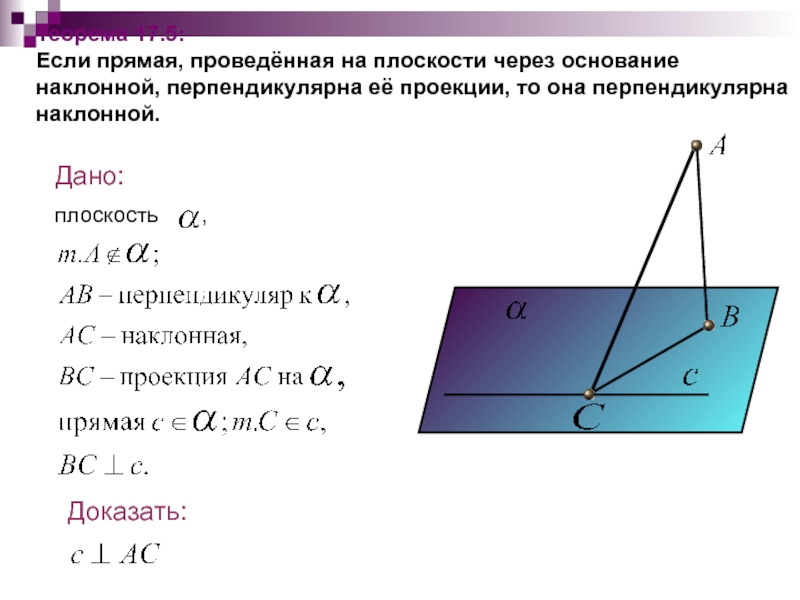
Дано:
прямая
т.А а
А
Доказать:
I)
II)
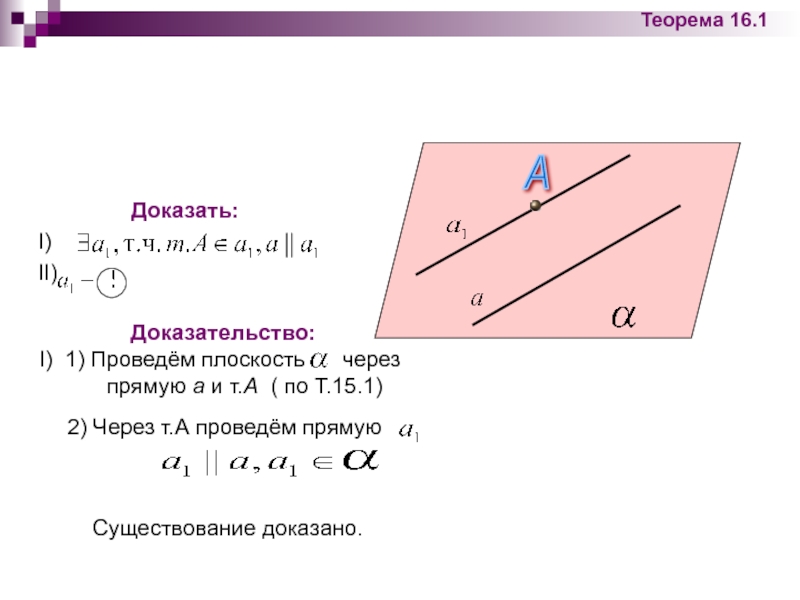
Теорема 16.1: Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.
Слайд 17Доказательство:
I) 1) Проведём плоскость через
Доказать:
I)
II)
А
2) Через т.А проведём прямую
Существование доказано.
Теорема 16.1
Слайд 18
А
5) Получили, что через прямую а и точку А проходит 2
Теорема доказана.
Теорема 16.1
Слайд 19Признак параллельности прямых
Теорема 16.2:
Две прямые, параллельные третьей прямой, параллельны.
b
c
Рассмотрим случай,
Дано:
Доказать:
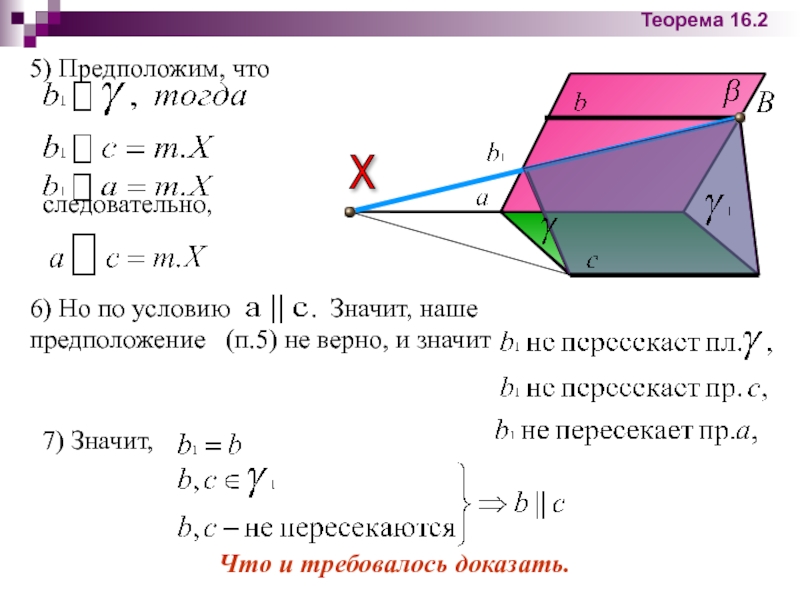
Слайд 215) Предположим, что
следовательно,
Что и требовалось доказать.
Х
6) Но по
7) Значит,
Теорема 16.2
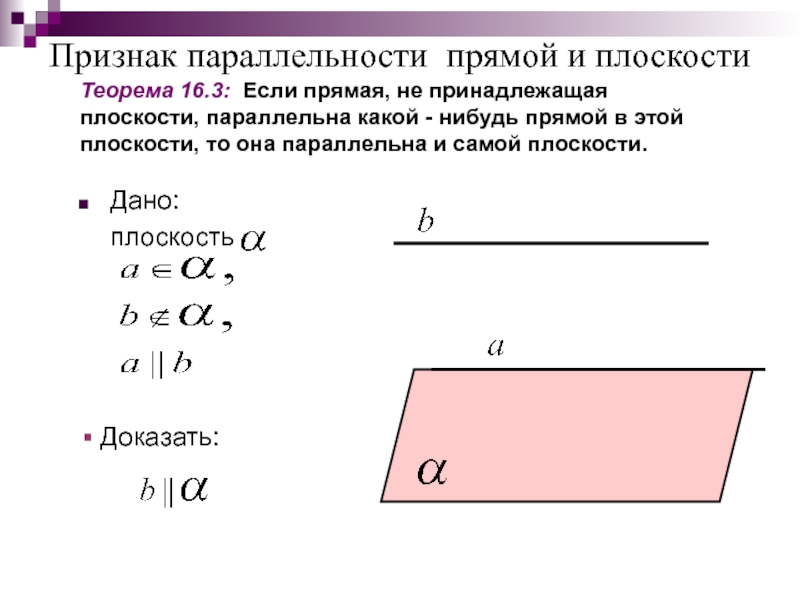
Слайд 22Признак параллельности прямой и плоскости
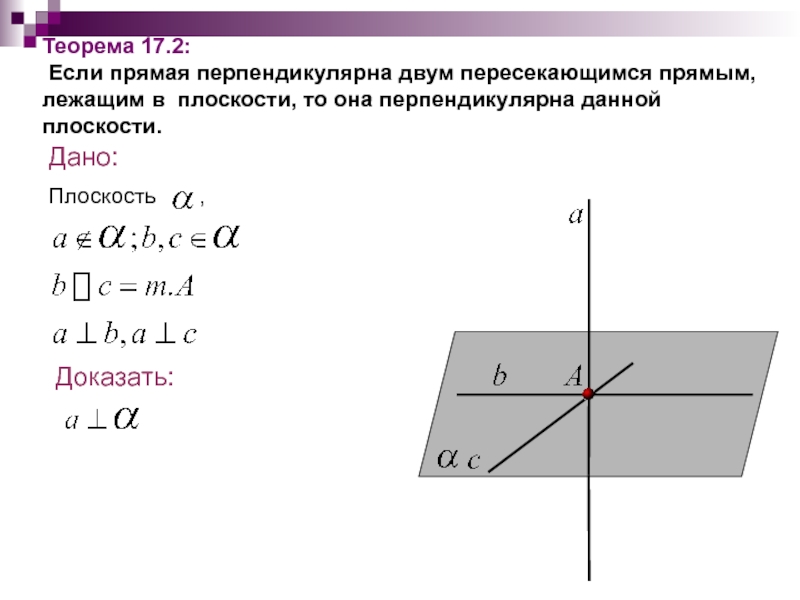
Дано:
Теорема 16.3: Если прямая, не принадлежащая плоскости, параллельна какой - нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Доказать:
Слайд 23
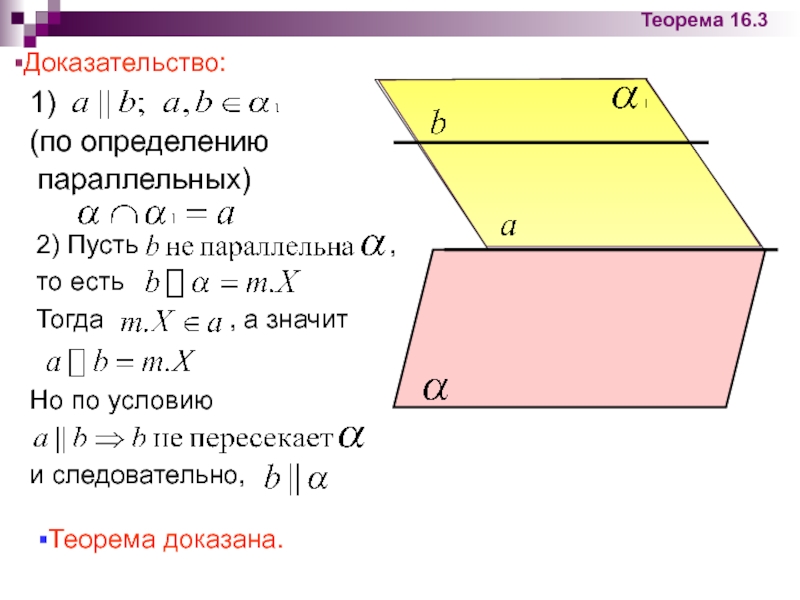
1)
(по определению
параллельных)
Доказательство:
2) Пусть
то есть
Тогда , а значит
Но по условию
и следовательно,
Теорема доказана.
Теорема 16.3
Слайд 24
А
c
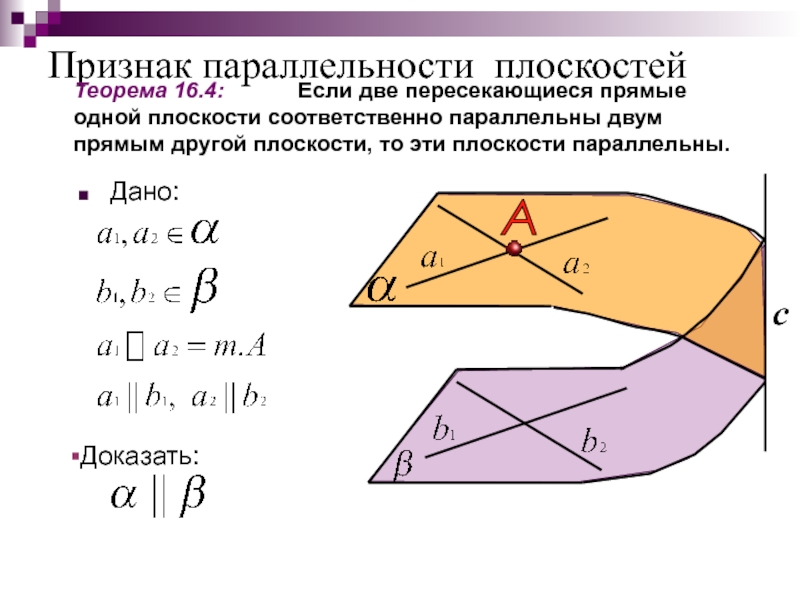
Признак параллельности плоскостей
Дано:
Теорема 16.4: Если
Доказать:
Слайд 25
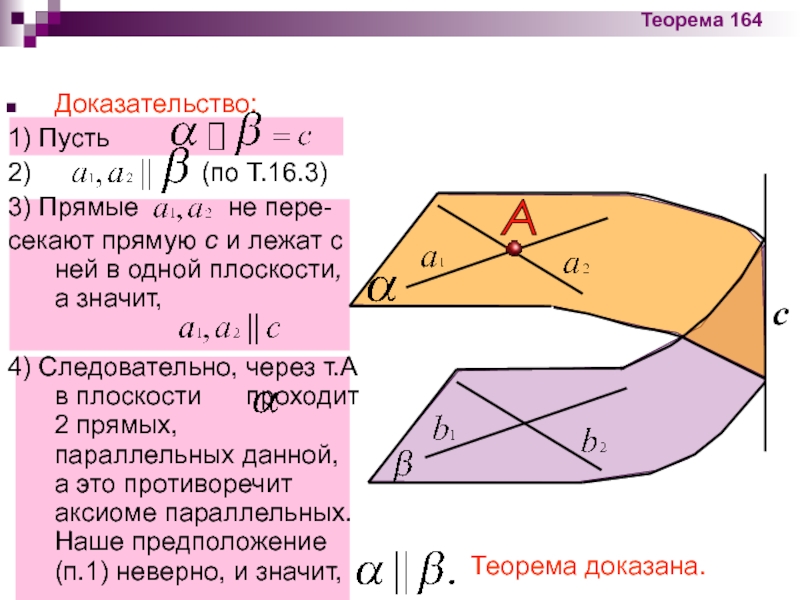
Доказательство:
1) Пусть
2)
3) Прямые не пере-
секают прямую с и лежат с ней в одной плоскости, а значит,
4) Следовательно, через т.А в плоскости проходит 2 прямых, параллельных данной, а это противоречит аксиоме параллельных. Наше предположение (п.1) неверно, и значит,
А
c
Теорема доказана.
Теорема 164
Слайд 26Существование плоскости, параллельной данной плоскости
Теорема 16.5:
А
Дано:
плоскость
Доказать:
1)
2)
(единственность мы доказывать не будем)
Слайд 271) Возьмём произвольные прямые
2) Через точку А проведём прямые
3) Проведём плоскость
через прямые
4) По Т.16.4 .
Теорема доказана.
Доказательство:
А
В
Теорема 16.5
Слайд 28
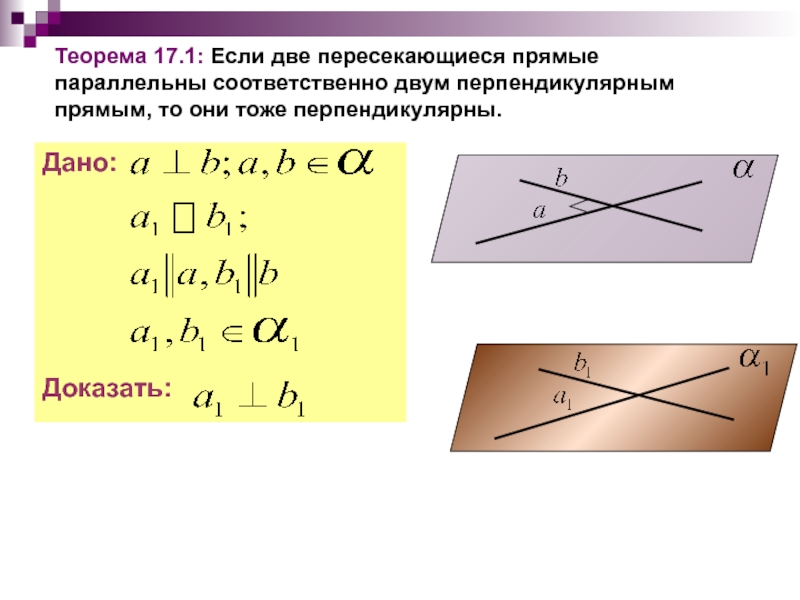
Теорема 17.1: Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым,
Дано:
Доказать:
Слайд 29
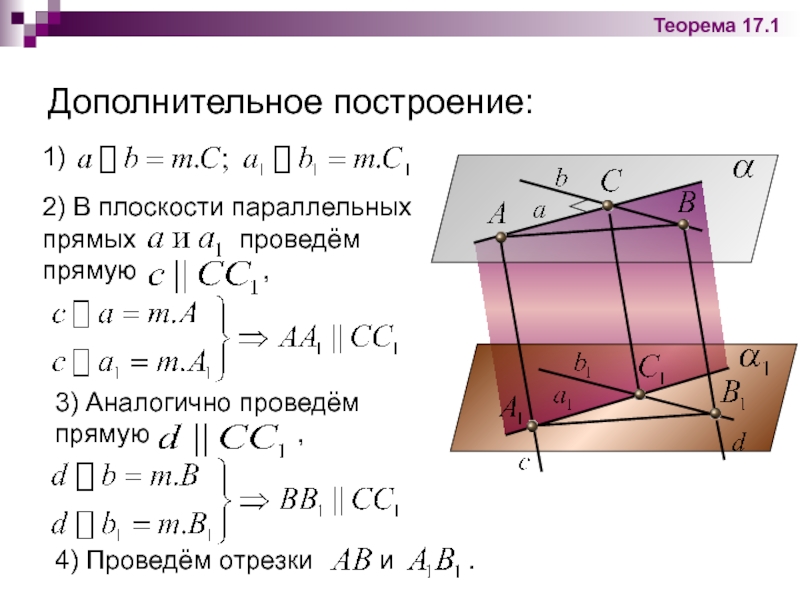
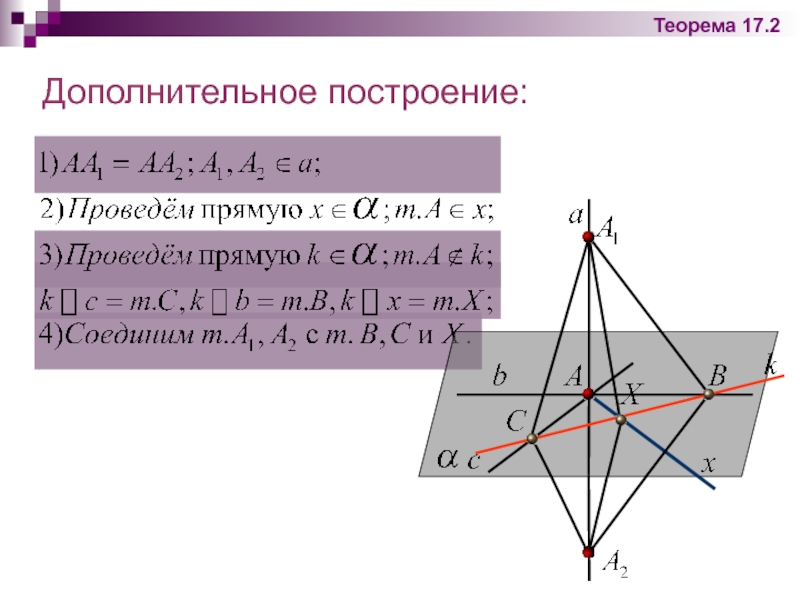
Дополнительное построение:
1)
2) В плоскости параллельных прямых
3) Аналогично проведём прямую ,
4) Проведём отрезки и .
Теорема 17.1
Слайд 304) Рассмотрим четырёхугольник
-по построению
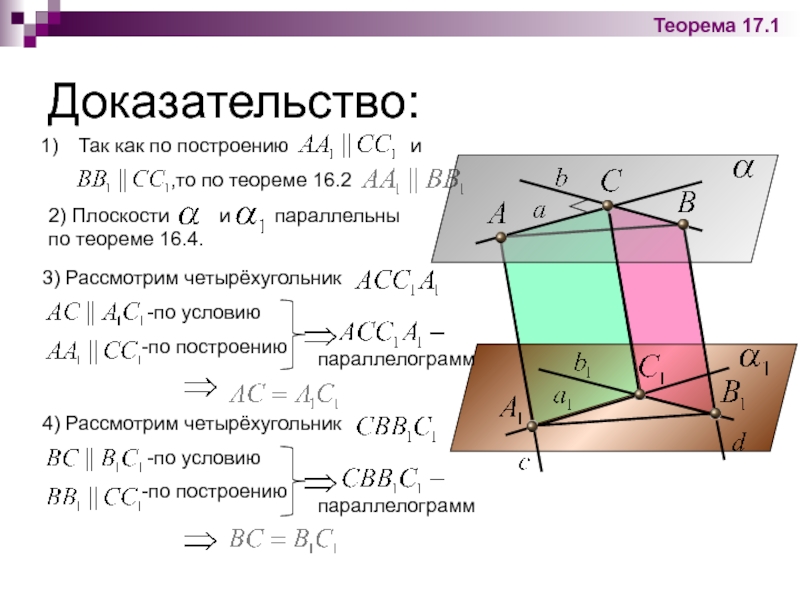
Доказательство:
Теорема 17.1
Так как по построению и
,то по теореме 16.2
2) Плоскости и параллельны по теореме 16.4.
3) Рассмотрим четырёхугольник
-по условию
-по построению
параллелограмм
параллелограмм
Слайд 31
Доказательство:
Теорема 17.1
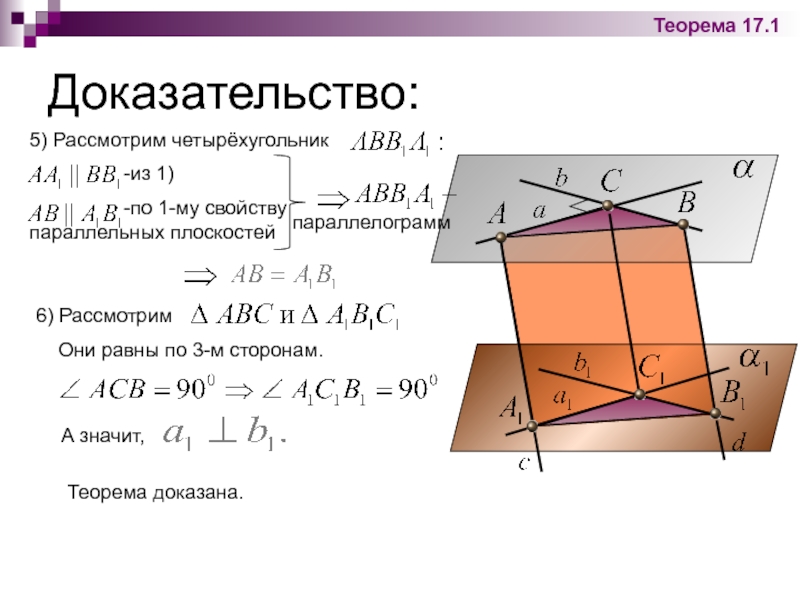
5) Рассмотрим четырёхугольник
-по 1-му свойству параллельных плоскостей
параллелограмм
6) Рассмотрим
Они равны по 3-м сторонам.
А значит,
Теорема доказана.
Слайд 32
Теорема 17.2:
Если прямая перпендикулярна двум пересекающимся прямым,
Слайд 35
Теорема 17.3:
Если плоскость перпендикулярна одной из двух
Слайд 362) Проведём в плоскости прямую
Дополнительное построение:
Теорема 17.3
1) Проведём в плоскости
3) Так как , то по определению перпендикулярности прямой и плоскости.
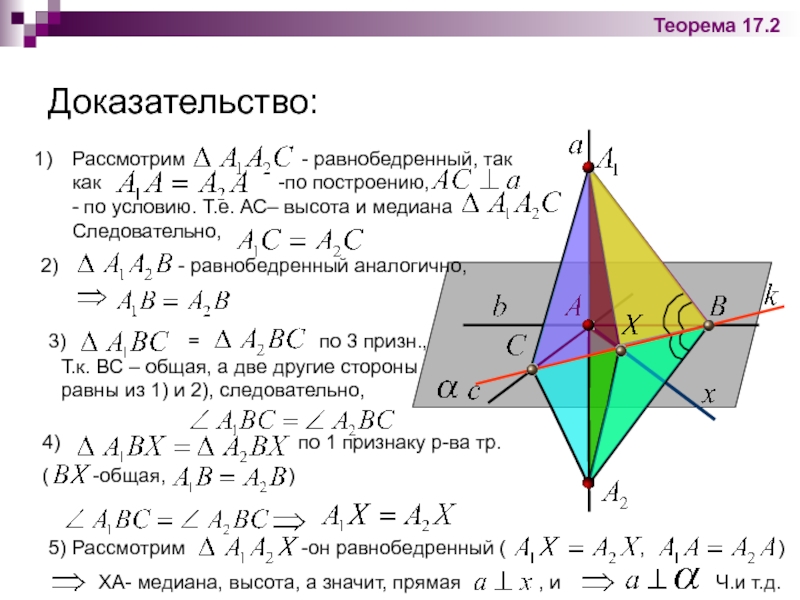
Слайд 37Доказательство:
Теорема 17.3
по условию
-по
по теореме 17.1.
1) и
Но так как выбор прямой был произволен, то
Теорема доказана.
Слайд 39
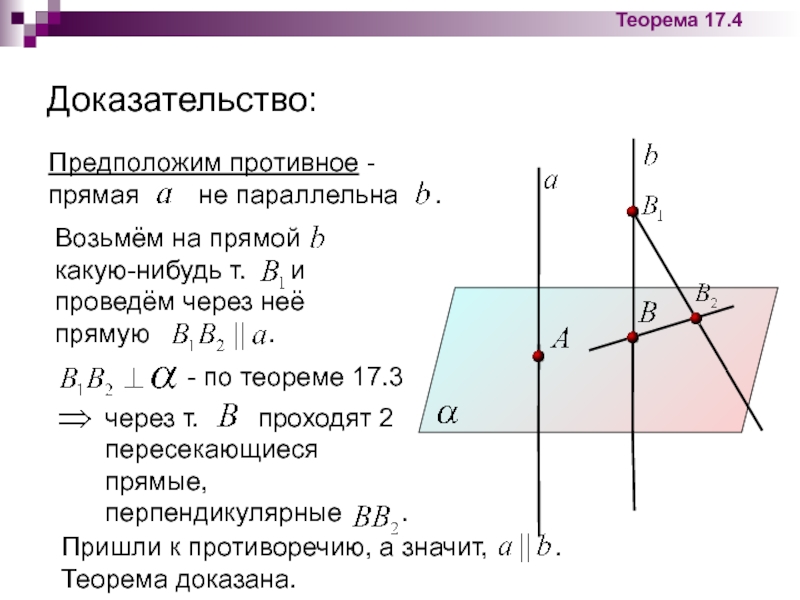
Доказательство:
Теорема 17.4
Предположим противное - прямая не параллельна
Возьмём на прямой какую-нибудь т. и проведём через неё прямую .
- по теореме 17.3
через т. проходят 2 пересекающиеся прямые, перпендикулярные .
Пришли к противоречию, а значит, . Теорема доказана.
Слайд 40
Теорема 17.5:
Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна
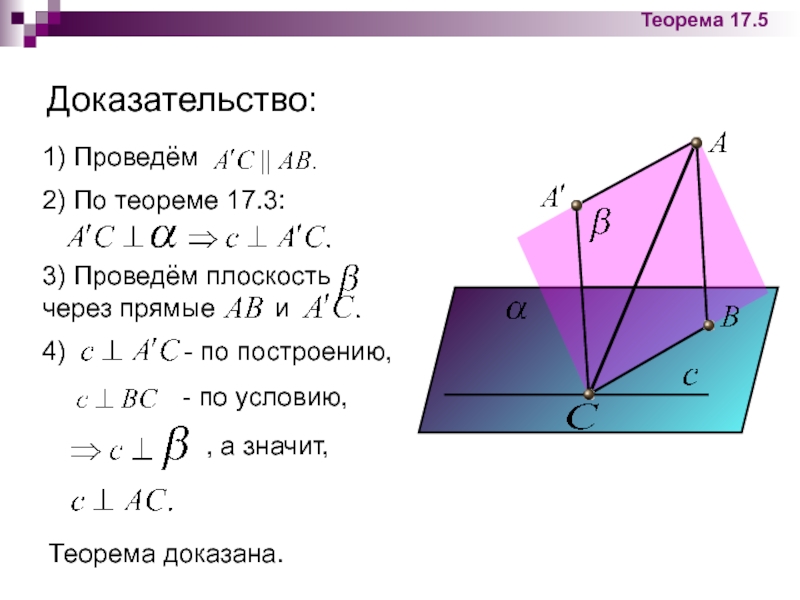
Слайд 41Доказательство:
Теорема 17.5
1) Проведём
2) По теореме 17.3:
3) Проведём плоскость через
4) - по построению,
- по условию,
, а значит,
Теорема доказана.
Слайд 42
Теорема 17.6:
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то
Слайд 43Доказательство:
Теорема 17.6
1)
2) Проведём на пл. через т. О прямую
3) Проведём плоскость
- по построению
- по условию,
(т.к. ), а значит, пл. пересекает пл-ти и
по перпендикулярным прямым, по определению перпендикулярности плоскостей. Теорема доказана.