частинами у визначеному інтегралі
Невласні інтеграли
Геометричні застосування визначеного інтегралу
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Визначений інтеграл презентация
Содержание
- 1. Визначений інтеграл
- 2. Якщо функція f(x) неперервна на відрізку [a;b](де
- 3. Означення Якщо по різному ділити відрізок [a;b]
- 4. Властивості визначеного інтеграла 1) При перестановці меж
- 5. 5) Постійний множник k можна виносити за
- 6. Приклад 1. Приклад 2.
- 7. 2. Метод заміни змінної у визначеному інтегралі.
- 8. Приклад 3.
- 9. Інтегрування частинами у визначеному інтегралі. Якщо
- 10. Приклад 4.
- 11. 3. Невласні інтеграли. а) Інтеграли з нескінченними
- 12. Тобто:
- 13. Приклад. Обчислити інтеграл: Розв’язок:
- 14. б) Інтеграли від розривних функцій. Якщо функція
- 15. Якщо функція f(x) має розрив у точці
Слайд 1Визначений інтеграл
План
Означення визначеного інтеграла та його властивості
Метод заміни змінної та інтегрування
Слайд 2Якщо функція f(x) неперервна на відрізку [a;b](де a < b), і
якщо:
Розбити цей відрізок на n частинних відрізків довжиною Δx1, Δx2, ..., Δxn;
Вибрати на кожному частинному відрізку по одній довільній точці ε1, ε2, ..., εn;
Обчислити значення функції f(x) у вибраних точках;
Скласти суму
то вона називається інтегральною сумою f(x) на відрізку [a;b].
Розбити цей відрізок на n частинних відрізків довжиною Δx1, Δx2, ..., Δxn;
Вибрати на кожному частинному відрізку по одній довільній точці ε1, ε2, ..., εn;
Обчислити значення функції f(x) у вибраних точках;
Скласти суму
то вона називається інтегральною сумою f(x) на відрізку [a;b].
Слайд 3Означення
Якщо по різному ділити відрізок [a;b] на n частинних відрізків і
по-різному вибирати на них по одній точці εi, то можна для будь-якої неперервної функції f(x) і будь-якого заданого відрізка [a;b] скласти нескінченну множину різних інтегральних сум.
При цьому виявляється, що всі ці інтегральні суми при необмеженому зростанні n при прямуванні до нуля найбільшої із довжин частинного відрізка, мають одну і ту ж границю.
Ця границя всіх інтегральних сум функції f(x) на відрізку [a;b] називається визначеним інтегралом від f(x) в межах від a до b та позначається:
При цьому виявляється, що всі ці інтегральні суми при необмеженому зростанні n при прямуванні до нуля найбільшої із довжин частинного відрізка, мають одну і ту ж границю.
Ця границя всіх інтегральних сум функції f(x) на відрізку [a;b] називається визначеним інтегралом від f(x) в межах від a до b та позначається:
Слайд 4Властивості визначеного інтеграла
1) При перестановці меж інтегрування знак інтегралу змінюється на
протилежний:
2) Інтеграл з однаковими межами дорівнює нулю:
3) Відрізок інтегрування можна розбити на частини:
4) Інтеграл від алгебраїчної суми функцій дорівнює сумі інтегралів від кожного доданку:
2) Інтеграл з однаковими межами дорівнює нулю:
3) Відрізок інтегрування можна розбити на частини:
4) Інтеграл від алгебраїчної суми функцій дорівнює сумі інтегралів від кожного доданку:
Слайд 55) Постійний множник k можна виносити за знак інтеграла:
Для обчислення визначеного
інтеграла використовується формула Ньютона-Лейбніца:
(1)
тобто, визначений інтеграл дорівнює різниці значень невизначеного інтеграла при верхній та нижній межах інтегрування.
(1)
тобто, визначений інтеграл дорівнює різниці значень невизначеного інтеграла при верхній та нижній межах інтегрування.
Слайд 72. Метод заміни змінної у визначеному інтегралі.
Якщо визначений інтеграл
перетворюється за допомогою підстановки:
в інший інтеграл, з новою змінною t, то задані межі: змінюються новими межами:
, які визначаються з вибраної підстановки, тобто з рівнянь:
Якщо неперервні на відрізку:
то:
(2)
в інший інтеграл, з новою змінною t, то задані межі: змінюються новими межами:
, які визначаються з вибраної підстановки, тобто з рівнянь:
Якщо неперервні на відрізку:
то:
(2)
Слайд 9Інтегрування частинами у визначеному інтегралі.
Якщо підінтегральний вираз у визначеному інтегралі
можна представити у вигляді добутку двох співмножників: u, dv, то для обчислення визначеного інтегралу треба скористатися формулою інтегрування частинами:
Слайд 113. Невласні інтеграли.
а) Інтеграли з нескінченними межами.
Означення. Якщо існує скінченна границя:
то цю границю називають невласним інтегралом від функції ,
в інтервалі і позначають:
в інтервалі і позначають:
Слайд 12Тобто:
(3)
У цьому випадку кажуть, що інтеграл існує або він є збіжним. Якщо не має
скінченної границі, то кажуть, що
не існує, або він розбіжний.
Аналогічно визначаються:
У цьому випадку кажуть, що інтеграл існує або він є збіжним. Якщо не має
скінченної границі, то кажуть, що
не існує, або він розбіжний.
Аналогічно визначаються:
Слайд 14б) Інтеграли від розривних функцій.
Якщо функція
визначена та неперервна у відкритому інтервалі: ,а у точці x=b невизначена, або має розрив, тоді інтеграл визначають наступним чином:
Якщо границя, що стоїть у правій частині рівності, існує, то інтеграл називають невласний збіжний інтеграл, у протилежному випадку – розбіжний.
У випадку, коли функція має розрив у точці x = a відрізка [a, b], то за означенням
Якщо границя, що стоїть у правій частині рівності, існує, то інтеграл називають невласний збіжний інтеграл, у протилежному випадку – розбіжний.
У випадку, коли функція має розрив у точці x = a відрізка [a, b], то за означенням
Слайд 15Якщо функція f(x) має розрив у точці x = c всередині
відрізка [a, b], то вважаємо, що
коли обидва невласних інтеграли у правій частині рівності існують.
Приклад: Обчислити
коли обидва невласних інтеграли у правій частині рівності існують.
Приклад: Обчислити

, і якщо:Розбити цей відрізок на](/img/tmb/2/196151/9a721d8d17e1e17c36a309c20c58e8d8-800x.jpg)
![ОзначенняЯкщо по різному ділити відрізок [a;b] на n частинних відрізків і по-різному вибирати на них](/img/tmb/2/196151/9996246bb81af0c4a10a9696c1c812a5-800x.jpg)


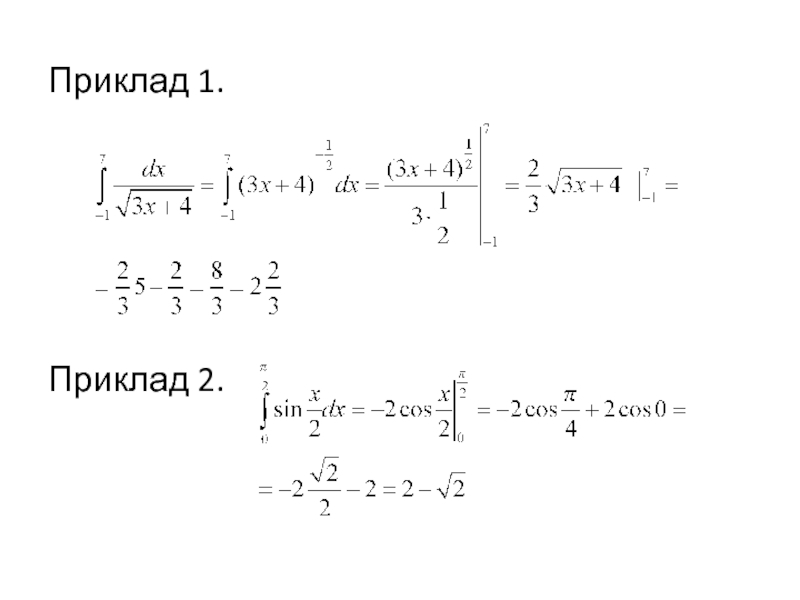








![Якщо функція f(x) має розрив у точці x = c всередині відрізка [a, b], то](/img/tmb/2/196151/97f9fcc33e563446147dc4b22e42b161-800x.jpg)





