- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Випадкові величини. Визначення випадкової величини (лекція 6) презентация
Содержание
- 1. Випадкові величини. Визначення випадкової величини (лекція 6)
- 2. Визначення випадкової величини Випадкова величина –
- 3. Дискретна випадкова величина та способи її задання
- 4. Дискретна випадкова величина та способи її задання
- 5. Числові характеристики дискретної випадкової величини Математичне сподівання
- 6. Основні закони розподілу дискретних випадкових величин Формула
- 7. Основні закони розподілу дискретних випадкових величин Формулу
- 8. Основні закони розподілу дискретних випадкових величин За
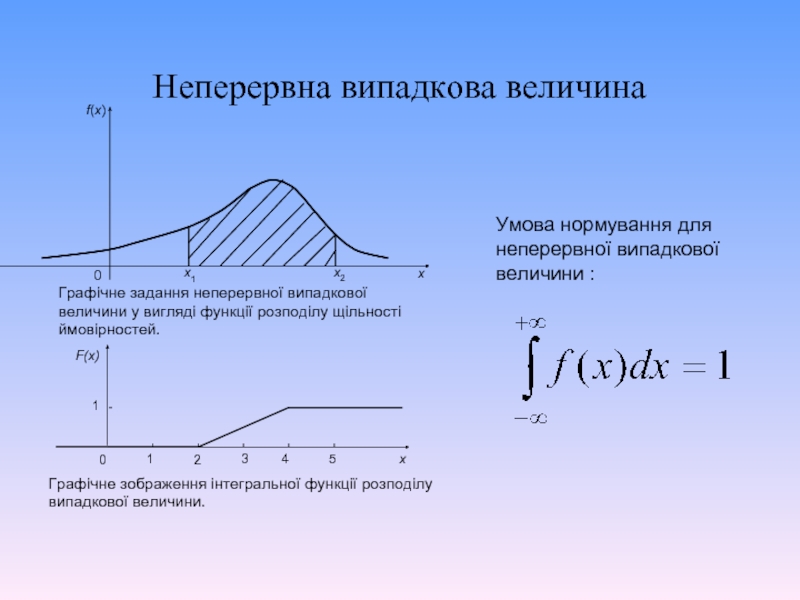
- 9. Неперервна випадкова величина. Способи її задання Неперервною
- 10. Неперервна випадкова величина Умова нормування для неперервної випадкової величини :
- 11. Числові характеристики неперервної випадкової величини Математичне сподівання:
- 12. Основні закони розподілу неперервних випадкових величин 1.
- 13. Основні закони розподілу неперервних випадкових величин 2.
- 14. Основні закони розподілу неперервних випадкових величин 3.
- 15. Стандартна функція Лапласа Якщо в функції Гаусса
- 16. Основні закони розподілу неперервних випадкових величин
- 17. ДЯКУЮ ЗА УВАГУ!
Слайд 2Визначення випадкової величини
Випадкова величина – це величина, що приймає в
Розрізняють дискретні та неперервні випадкові величини.
Слайд 3Дискретна випадкова величина та способи її задання
Дискретною випадковою
Для визначення дискретної випадкової величини задають закон її розподілу (чи ряд розподілу), тобто всі можливі значення випадкової величини та відповідні їм ймовірності:
Слайд 4Дискретна випадкова величина та способи її задання
Події, що полягають в тому,
Слайд 5Числові характеристики дискретної випадкової величини
Математичне сподівання
Дисперсія
, де
Середнє квадратичне відхилення
Слайд 6Основні закони розподілу дискретних випадкових величин
Формула Бернуллі:
Сукупність отриманих ймовірностей Рn(0),
Слайд 7Основні закони розподілу дискретних випадкових величин
Формулу Муавра-Лапласа використовують для схеми Бернуллі,
Ймовірності визначають за формулами:
а)
- локальна формула Лапласа;
б)
- інтегральна формула Лапласа, де Ф(z)- інтегральна функція Лапласа
Слайд 8Основні закони розподілу дискретних випадкових величин
За тих же умов, але коли
При цьому:
Слайд 9Неперервна випадкова величина. Способи її задання
Неперервною випадковою величиною називається випадкова величина,
Інтегральна функція розподілу неперервної випадкової величини:
Диференціальна функція розподілу неперервної випадкової величини (функція щільності розподілу):
Слайд 11Числові характеристики неперервної випадкової величини
Математичне сподівання:
Дисперсія :
де
Середнє квадратичне відхилення :
Ймовірність попадання у проміжок :
Слайд 12Основні закони розподілу неперервних випадкових величин
1. Рівномірний розподіл:
Диференціальна функція розподілу -
Інтегральна
Слайд 13Основні закони розподілу неперервних випадкових величин
2. Показниковий (експонентний) розподіл неперервної випадкової
Диференціальна функція розподілу -
Інтегральна функція розподілу -
Слайд 14Основні закони розподілу неперервних випадкових величин
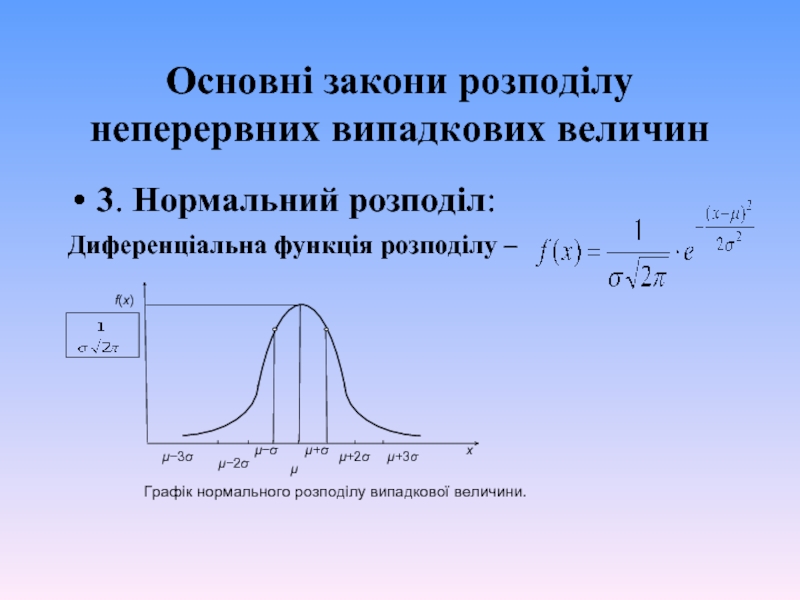
3. Нормальний розподіл:
Диференціальна функція розподілу –
Слайд 15Стандартна функція Лапласа
Якщо в функції Гаусса взяти
Слайд 16Основні закони розподілу неперервних випадкових величин
3. Нормальний розподіл
Ймовірність попадання нормально
де - інтегральна функція Лапласа, її значення знаходяться за таблицею.
Правило трьох сигм: якщо випадкова величина нормально розподілена, то майже достовірно, тобто з імовірністю, близької до одиниці , ії значення лежать на проміжку [μ−3σ; μ+3σ].