- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виды многогранников презентация
Содержание
- 1. Виды многогранников
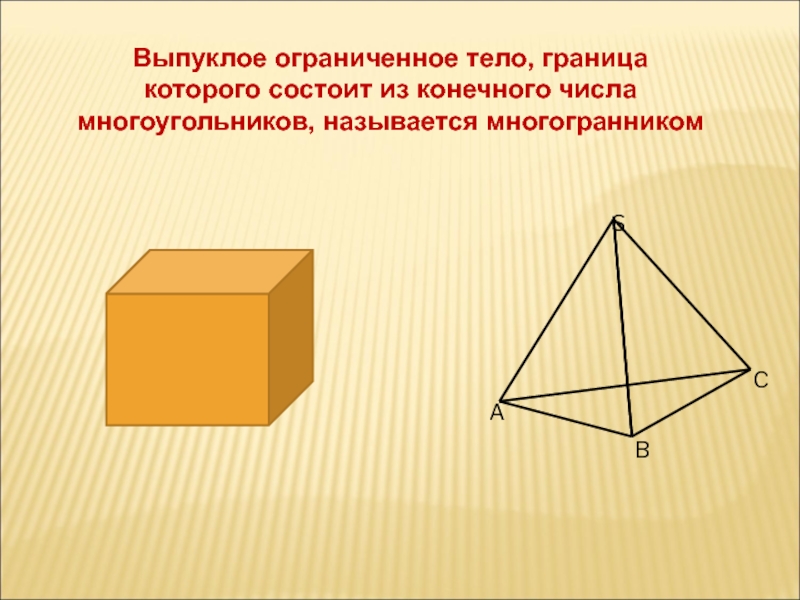
- 2. Выпуклое ограниченное тело, граница которого состоит из конечного числа многоугольников, называется многогранником
- 3. ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани
- 4. Многогранник, две грани которого – одноименные
- 5. ВИДЫ ПРИЗМ Призма Ребро перпендикулярно основанию Ребро
- 6. ПРИЗМА, ОСНОВАНИЕ КОТОРОЙ – ПАРАЛЛЕЛОГРАММ, НАЗЫВАЕТСЯ ПАРАЛЛЕЛЕПИПЕДОМ. Sпов.парал. = Sбок. + 2Sосн.
- 7. ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВ Параллелепипеды Ребро перпендикулярно основанию Ребро
- 8. , C Многогранник, одна из граней которого
- 9. ВИДЫ ПИРАМИД Пирамида Основание - правильный многоугольник
- 10. ЗАДАНИЯ ДЛЯ ЗАЧЕТА Вариант А1 1. Верно
- 11. Вариант А1 7. Верно ли, что все
- 12. ОТВЕТЫ К ЗАДАНИЯМ 1. Нет/да 2. Да/да
- 13. ИСПОЛЬЗОВАННЫЕ МАТЕРИАЛЫ: 1. «Геометрия» для 10-12 классов
- 14. Спасибо за внимание
Слайд 1МНОГОГРАННИКИ
Муниципальное общеобразовательное
учреждение
«Вечерняя /сменная/ общеобразовательная школа №8»
Учитель математики
Урусова
Слайд 2Выпуклое ограниченное тело, граница которого состоит из конечного числа многоугольников, называется
Слайд 3
ПРАВИЛЬНЫЙ МНОГОГРАННИК
- выпуклый многогранник, грани которого являются правильными многоугольниками с одним
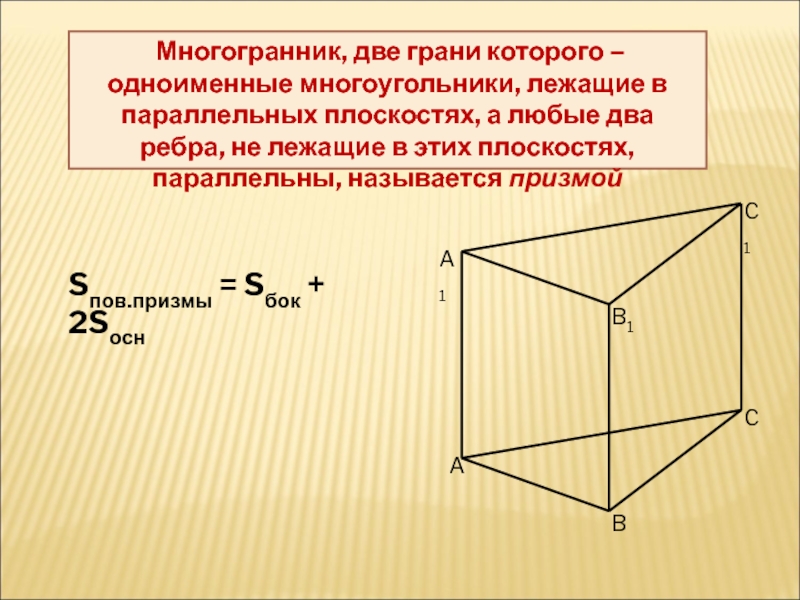
Слайд 4 Многогранник, две грани которого – одноименные многоугольники, лежащие в параллельных
Sпов.призмы = Sбок + 2Sосн
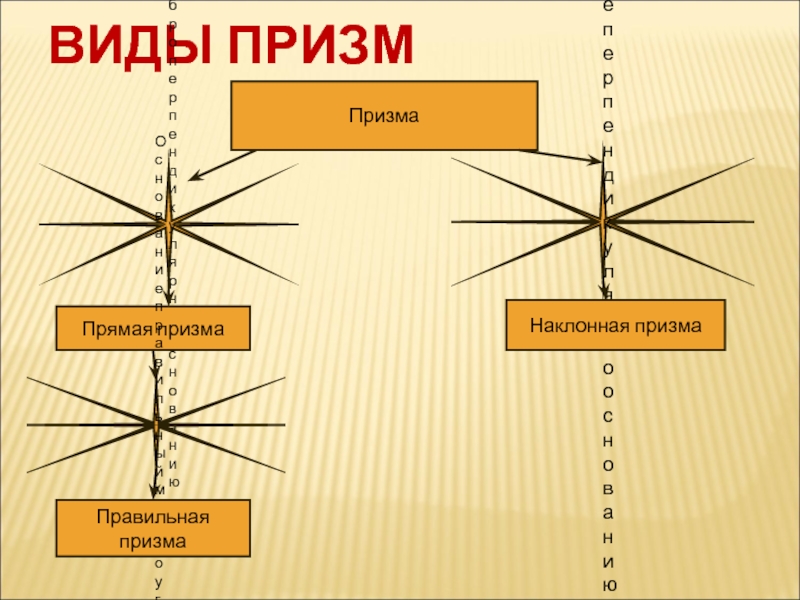
Слайд 5ВИДЫ ПРИЗМ
Призма
Ребро перпендикулярно основанию
Ребро не перпендикулярно основанию
Прямая призма
Наклонная призма
Основание правильный многоугольник
Правильная
Слайд 6ПРИЗМА, ОСНОВАНИЕ КОТОРОЙ – ПАРАЛЛЕЛОГРАММ, НАЗЫВАЕТСЯ ПАРАЛЛЕЛЕПИПЕДОМ.
Sпов.парал. = Sбок. + 2Sосн.
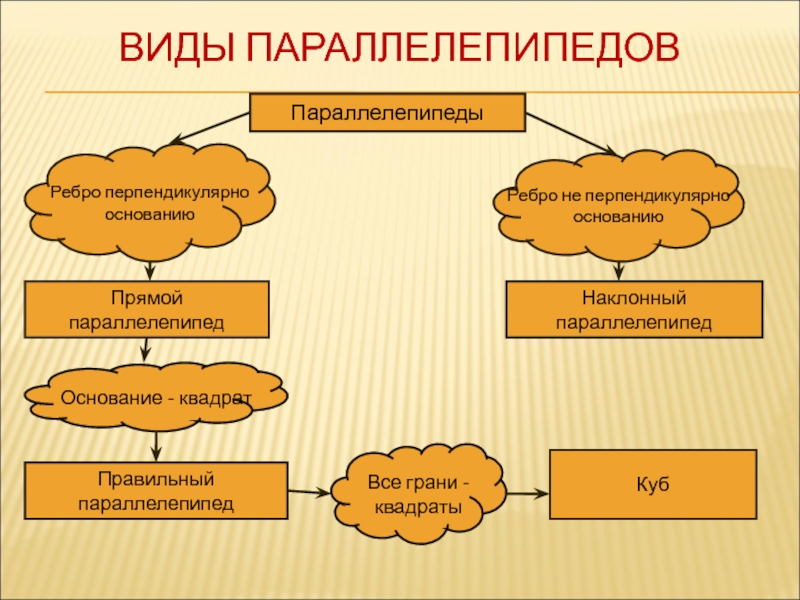
Слайд 7ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВ
Параллелепипеды
Ребро перпендикулярно основанию
Ребро не перпендикулярно основанию
Прямой параллелепипед
Наклонный параллелепипед
Основание - квадрат
Правильный
Все грани -квадраты
Куб
Слайд 8,
C
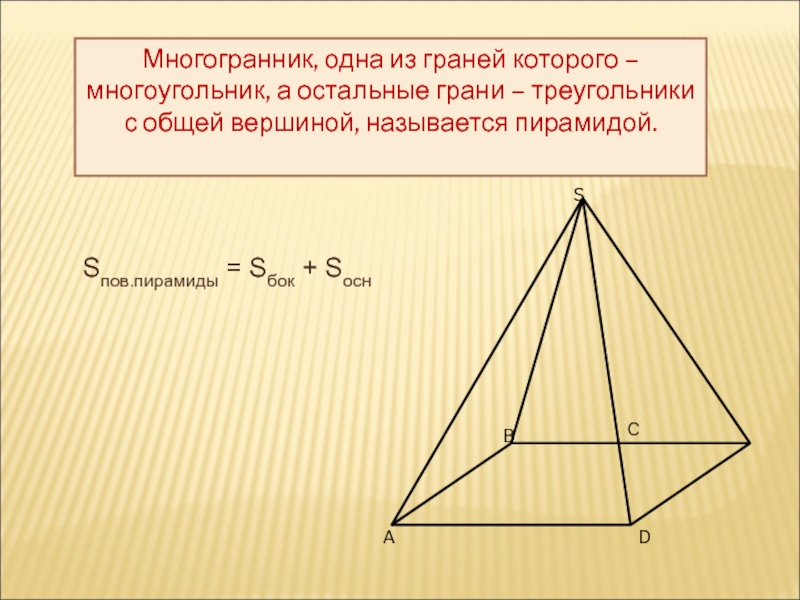
Многогранник, одна из граней которого – многоугольник, а остальные грани –
Sпов.пирамиды = Sбок + Sосн
Слайд 9ВИДЫ ПИРАМИД
Пирамида
Основание - правильный многоугольник
Основание не является правильным многоугольником
Высота восстановлена из
Правильная пирамида
Высота восстановлена не из центра основания
Неправильная пирамида
Слайд 10ЗАДАНИЯ ДЛЯ ЗАЧЕТА
Вариант А1
1. Верно ли, что основания любой призмы лежат
2. Может ли высота пирамиды быть больше ее бокового ребра?
3. Определите количество сторон многоугольника, лежащего в основании призмы, если она имеет семь граней.
4. Верно ли , что параллелепипед является четырехугольной призмой?
5. Верно ли, что правильная треугольная пирамида является правильным тетраэдром?
6. Верно ли, что если призма – правильная, то все ребра ее основания равны?
Вариант А2
1. Верно ли, что боковые ребра любой
призмы равны?
2. Может ли высота пирамиды совпадать с ее боковым ребром?
3. Определите количество сторон многоугольника, лежащего в основании пирамиды, если она имеет девять граней.
4. Верно ли, что все грани четырехугольной призмы являются параллелограммами?
5.Верно ли, что правильный тетраэдр является правильной треугольной пирамидой?
6. Верно ли, что если ребра основания прямой призмы равны, то она является правильной?
Слайд 11Вариант А1
7. Верно ли, что все грани прямой призмы – прямоугольники?
8.
9. Дайте определение правильной пирамиды.
10. Запишите формулу площади полной поверхности правильной призмы.
Вариант А2
7. Верно ли, что боковые грани наклонной призмы – параллелограммы?
8. Дайте определение правильной призмы.
9. Дайте определение апофемы правильной пирамиды.
10. Запишите формулу площади полной поверхности правильной пирамиды.
Слайд 13ИСПОЛЬЗОВАННЫЕ МАТЕРИАЛЫ:
1. «Геометрия» для 10-12 классов вечерней /сменной/ школы и самообразования,
2. «Устная геометрия» , 10-11 класс, А.П.Ершова, В.В. Голобородько, М. «Илекса», 2005г.
3. Интернет-ресурсы:
http://nips.riss-telecom.ru/poli/.