- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Верифікація моделі. (Тема 6) презентация
Содержание
- 1. Верифікація моделі. (Тема 6)
- 2. Зміст Показники якості моделі 2. Перевірка
- 3. Постановка задачі Формування вихідної інформації Аналіз
- 4. 1. Показники якості моделі Верифікація моделі—статистична
- 5. Для перевірки коректності побудови моделі визначають:
- 6. Стандартна похибка рівняння (точкова оцінка емпіричної дисперсії
- 7. Поправка на число ступенів свободи дає незміщену оцінку дисперсії залишків:
- 8. У поняття "тіснота зв'язку" (щільність) вкладається оцінка
- 9. Коефіцієнт детермінації показує, якою мірою варіація залежної
- 10. Інші формули: де
- 11. квадрат емпіричного коефіцієнта кореляції між двома
- 12. Коефіцієнт кореляції, або індекс кореляції, показує, наскільки
- 13. Іноді для спрощення розрахунків тісноту кореляційного зв'язку
- 14. Якщо зв'язок між результативним і вхідним показниками
- 15. 2. Перевірка значущості та довірчі інтервали.
- 16. Зауваження. У задачах регресійного аналізу важливе значення
- 17. Стосовно кожного статистичного результату висувається так звана
- 18. За заданим рівнем значущості множина допустимих значень
- 19. При перевірці гіпотез може бути допущена помилка,
- 20. R2 R2 0
- 21. Висувається нульова гіпотеза Н0 : R2 =
- 22. Альтернативною до неї є Н1: значення хоча
- 23. Для перевірки цих гіпотез застосовують F- критерій
- 24. Якщо Fтабл < Fексп нульова
- 25. У випадку парної регресії цей критерій розраховується за формулою:
- 26. Коефіцієнт кореляції, як вибіркова характеристика, перевіряється на
- 27. tексп порівнюється з табличним значенням t- розподілу
- 28. Можна визначити стандартні похибки оцінок параметрів моделі
- 29. cjj –відповідний діагональний елемент матриці похибок С
- 30. Статистичну значущість кожного параметра моделі можна перевірити
- 31. Довірчі інтервали для кожного параметра aj обчислюються
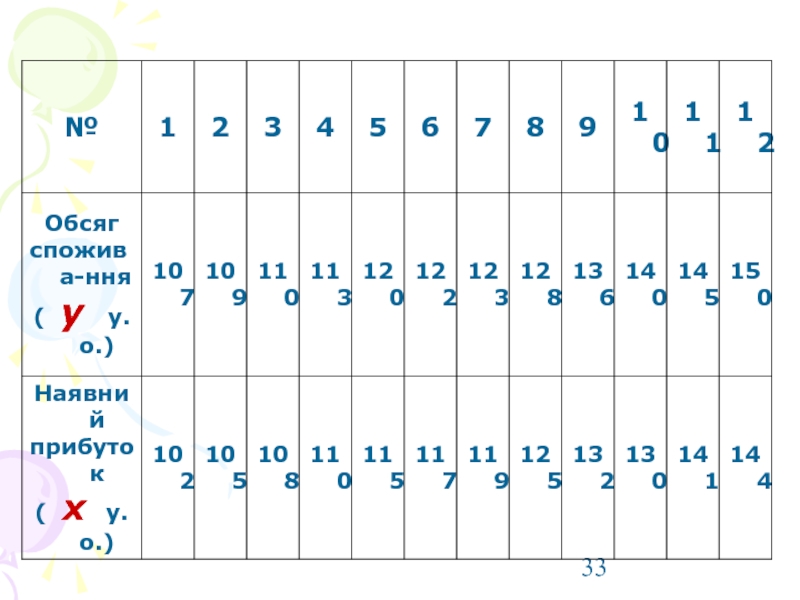
- 32. Завдання: Зробити аналіз залежності обсягу споживання y
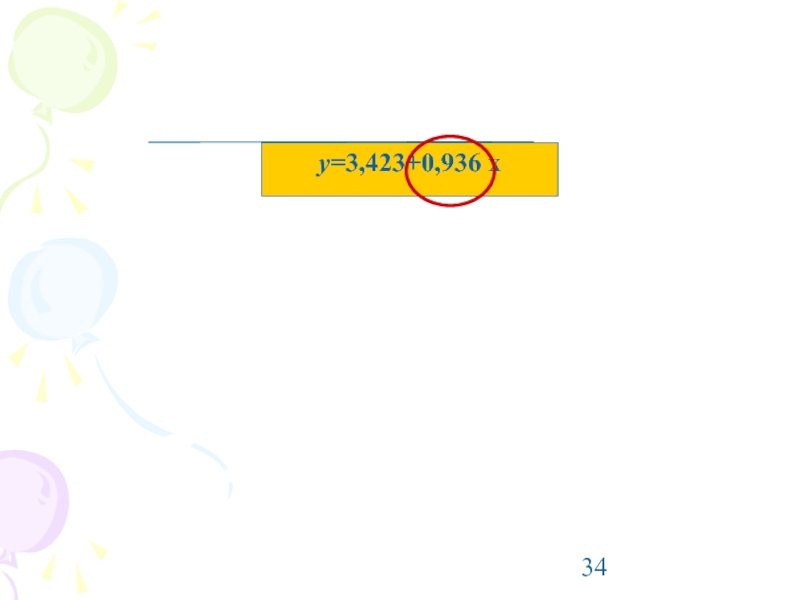
- 34. y=3,423+0,936 х
- 35. коефіцієнт кореляції R=0,9916067.
Слайд 1Тема 3
Верифікація моделі
Лектор: к.е.н., доцент кафедри економетрії та статистики ДЕМЧИШИН М.Я.
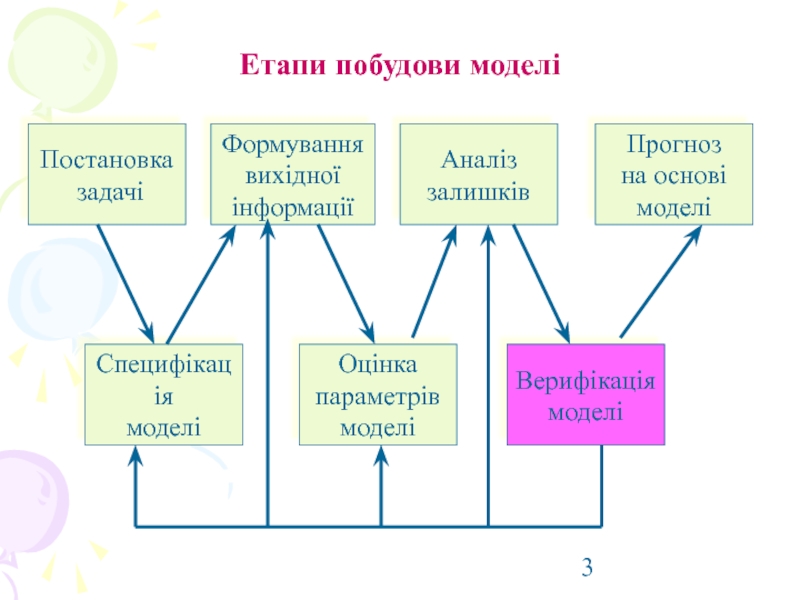
Слайд 3Постановка
задачі
Формування
вихідної
інформації
Аналіз
залишків
Прогноз
на основі
моделі
Специфікація
моделі
Оцінка
параметрів
моделі
Верифікація
моделі
Етапи побудови моделі
Слайд 41. Показники якості моделі
Верифікація моделі—статистична перевірка на адекватність моделі, тобто наскільки
Слайд 5Для перевірки коректності побудови моделі визначають:
• стандартну похибку рівняння;
• коефіцієнт детермінації;
• коефіцієнт
• стандартну похибку параметрів.
Слайд 6Стандартна похибка рівняння (точкова оцінка емпіричної дисперсії залишків)- характеризує абсолютну величину
Слайд 8 У поняття "тіснота зв'язку" (щільність) вкладається оцінка впливу незалежної змінної на
Під терміном "значимість зв'язку" (істотність, або значущість) розуміють оцінку відхилення вибіркових змінних від своїх значень у генеральній сукупності спостережень за допомогою статистичних критеріїв.
Слайд 9Коефіцієнт детермінації показує, якою мірою варіація залежної змінної (результативного показника) у
де
Слайд 10Інші формули:
де - розрахункові значення регресанда;
-загальна середня фактичних
даних результативного показника;
-фактичні індивідуальні значення результативного показника.
Слайд 11
квадрат емпіричного коефіцієнта кореляції між двома рядами спостережень (теоретичними значеннями регресанта
Слайд 12Коефіцієнт кореляції, або індекс кореляції, показує, наскільки значним є вплив змінної
і розраховується так:
Слайд 13Іноді для спрощення розрахунків тісноту кореляційного зв'язку характеризують коефіцієнтом кореляції, який
Слайд 14Якщо зв'язок між результативним і вхідним показниками лінійний, то використовується лінійний
Слайд 16Зауваження. У задачах регресійного аналізу важливе значення має припущення про нормальний
Певні перетворення нормально розподілених величин забезпечують їх розподіл за законом Стьюдента чи за законом Фішера: на підставі першого з них визначаються довірчі інтервали, а другий дає змогу оцінювати відношення двох випадкових величин.
Слайд 17 Стосовно кожного статистичного результату висувається так звана нульова гіпотеза (про рівність
Слайд 18За заданим рівнем значущості множина допустимих значень розбивається на дві неперетинні
Слайд 19 При перевірці гіпотез може бути допущена помилка, наприклад може бути відхилена
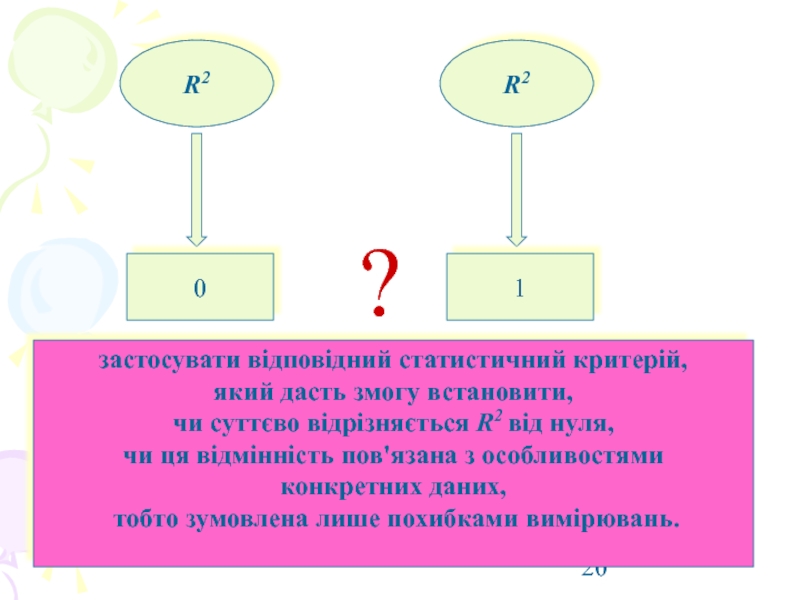
Слайд 20R2
R2
0
1
?
застосувати відповідний статистичний критерій,
який дасть змогу встановити,
чи
чи ця відмінність пов'язана з особливостями
конкретних даних,
тобто зумовлена лише похибками вимірювань.
Слайд 21Висувається нульова гіпотеза Н0 : R2 = О.
Це означає, що
У такому разі всі коефіцієнти при незалежних змінних мають дорівнювати нулю.
При цьому нульову гіпотезу можна подати у вигляді
Н0 :а1 =а2 =... = аn = 0.
Слайд 22Альтернативною до неї є Н1: значення хоча б одного параметра моделі
Слайд 23Для перевірки цих гіпотез застосовують F- критерій Фішера з n-m-1
яке порівнюють з табличним значенням розподілу Фішера при заданому рівні значущості α.
(Як правило, α = 0,05 або α = 0,01).
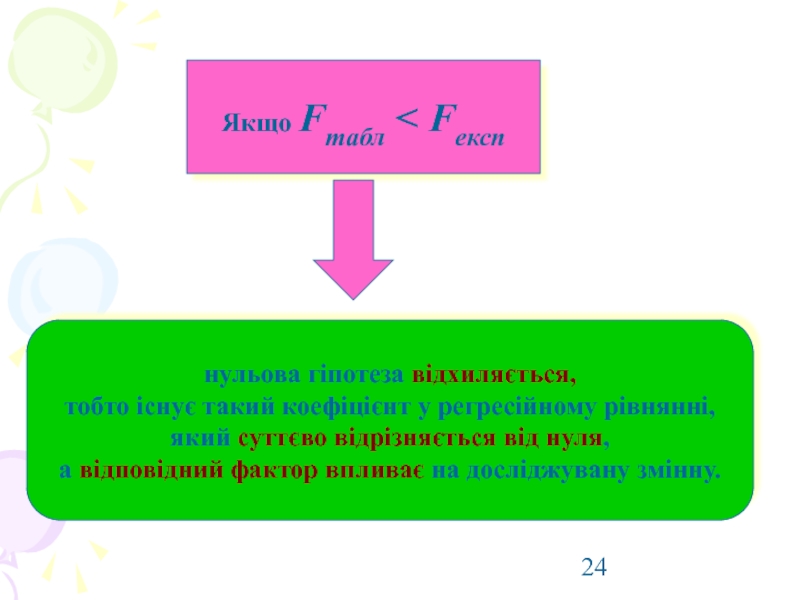
Слайд 24Якщо Fтабл < Fексп
нульова гіпотеза відхиляється,
тобто існує такий коефіцієнт
який суттєво відрізняється від нуля,
а відповідний фактор впливає на досліджувану змінну.
Слайд 26Коефіцієнт кореляції, як вибіркова характеристика, перевіряється на значущість за допомогою
t-критерію
Фактичне значення t статистики обчислюється за формулою
Слайд 27tексп порівнюється з табличним значенням t- розподілу з п – т
Якщо
можна зробити висновок, що коефіцієнт кореляції достовірний (значущий), а зв'язок між залежною змінною та всіма незалежними факторами суттєвий.
Слайд 28Можна визначити стандартні похибки оцінок параметрів моделі з урахуванням дисперсії залишків:
де
Слайд 29cjj –відповідний діагональний елемент матриці похибок С (матриця, обернена до матриці
Слайд 30Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При
Слайд 31Довірчі інтервали для кожного параметра aj обчислюються на основі його стандартної
Табличне значення t табл. , як і раніше, має n-m-1 ступенів свободи і рівень значущості α/2