- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устойчивость точки покоя. (Лекция 4) презентация
Содержание
- 1. Устойчивость точки покоя. (Лекция 4)
- 2. Математические определения устойчивости
- 4. Точки покоя системы
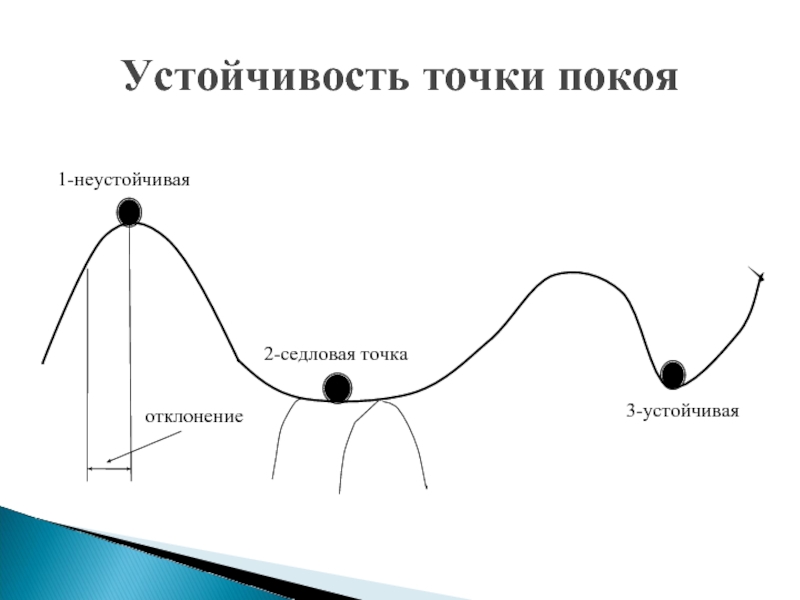
- 5. Устойчивость точки покоя
- 6. Пример расчета
- 9. Преобразование Лапласа
- 10. Свойства преобразования Лапласа
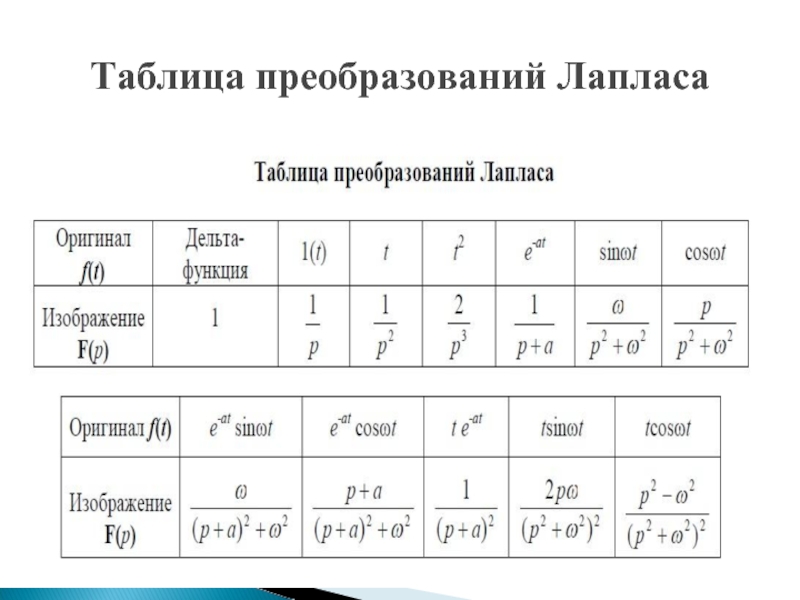
- 13. Таблица преобразований Лапласа
- 14. Восстановление оригиналов по изображениям
- 16. Примеры расчетов
- 17. Примеры расчетов
- 18. Использование преобразование Лапласа
- 19. Модель вход-выход an y(n)(t) + an-1 y(n-1)
- 20. Модель вход-выход
- 21. Передаточная функция системы
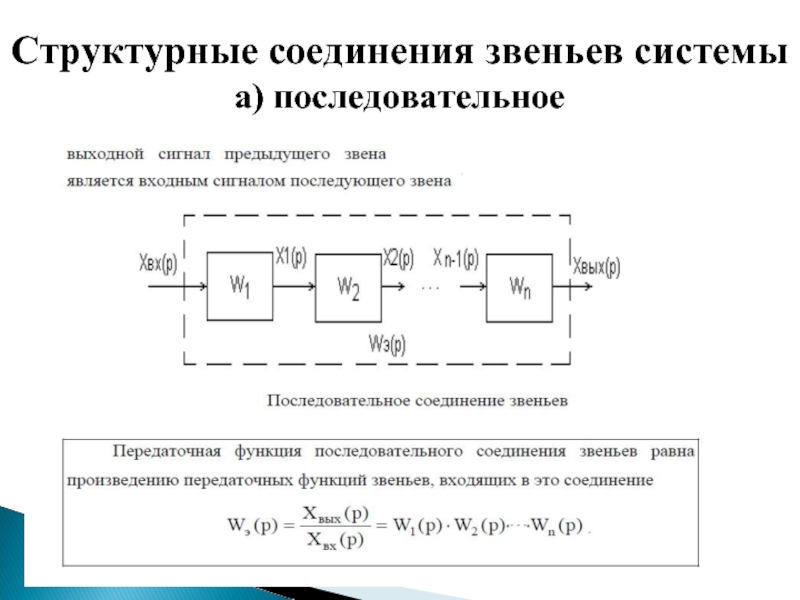
- 22. Структурные соединения звеньев системы а) последовательное
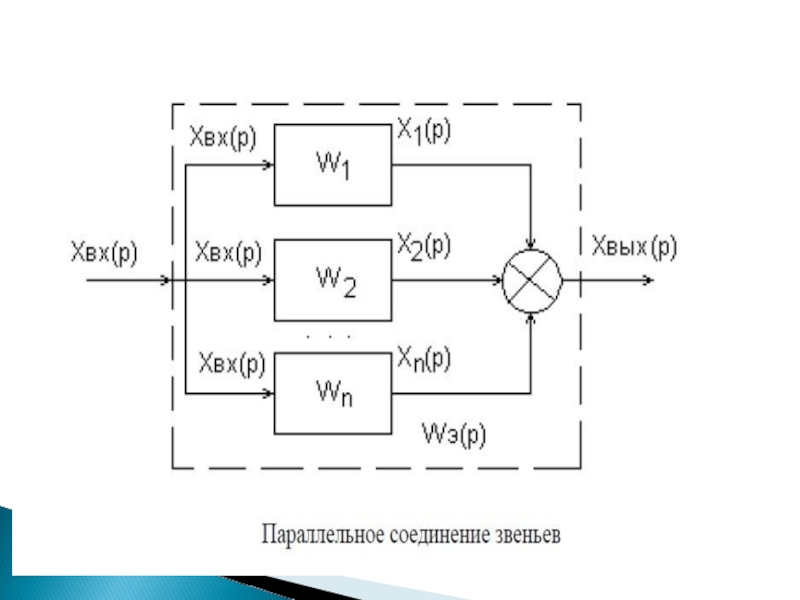
- 23. а) параллельное соединение
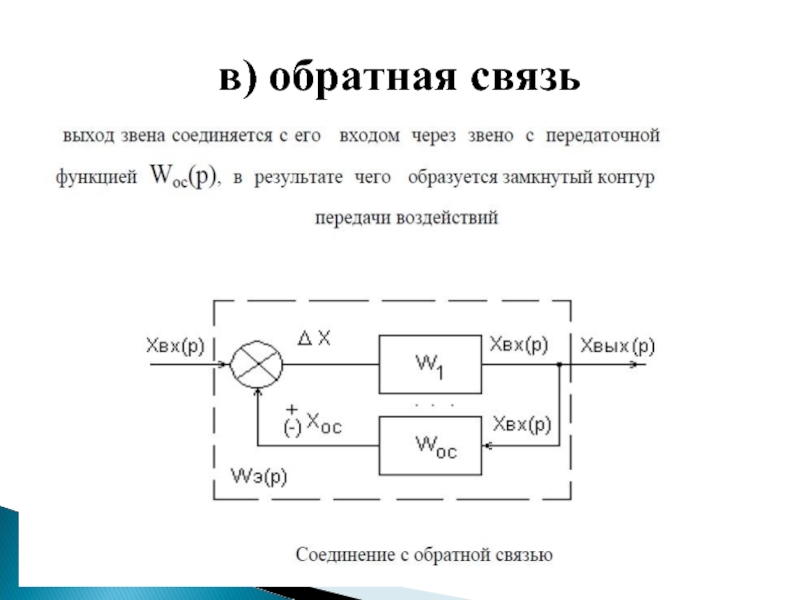
- 25. в) обратная связь
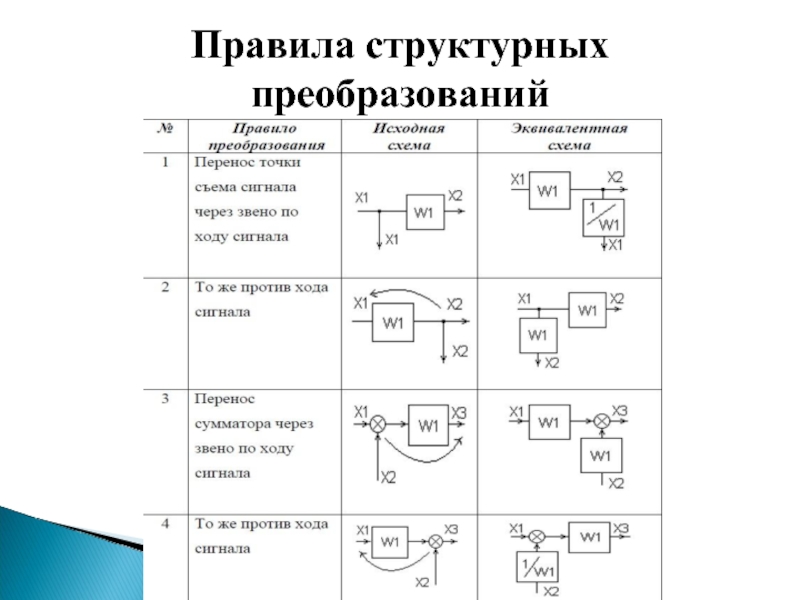
- 27. Правила структурных преобразований
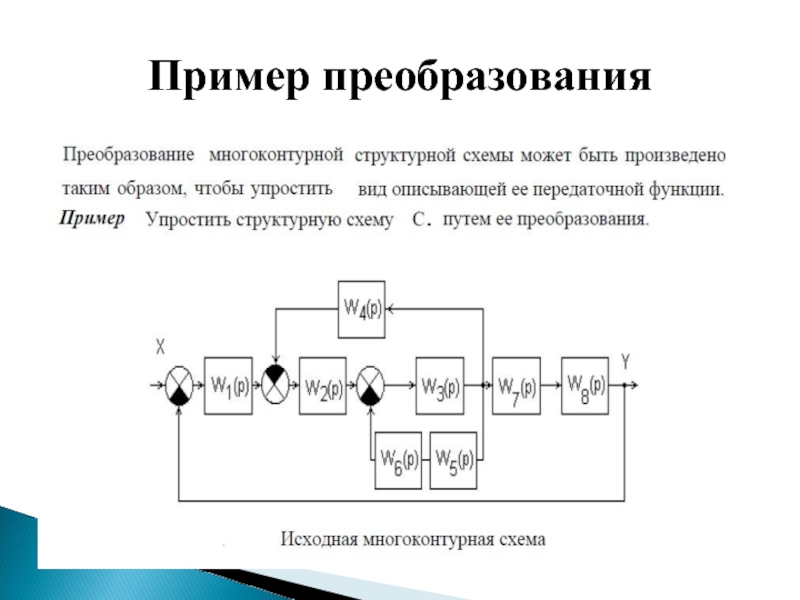
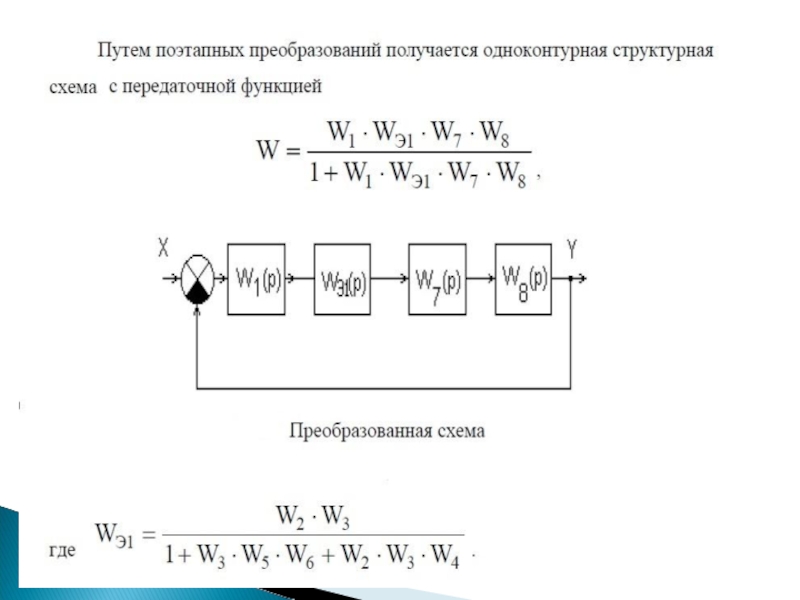
- 28. Пример преобразования
- 30. Переходная функция системы
- 31. Импульсная переходная функция
- 32. Функция Хэвисайда и δ-функция
- 33. Исследование систем
- 34. Схема и типовые воздействия в САУ
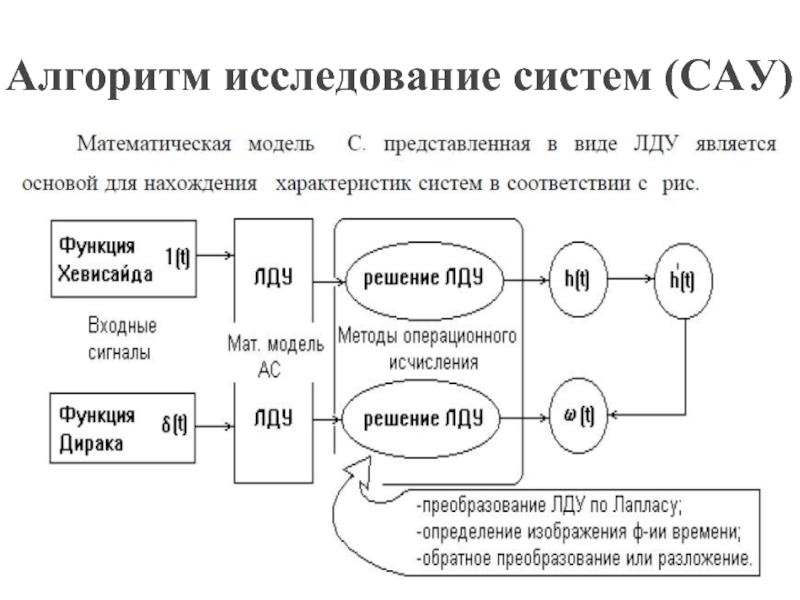
- 35. Алгоритм исследование систем (САУ)
- 36. Типы основных звеньев
- 37. Частотные характеристики систем (САУ)
- 38. Представление частотных ПФ
- 39. Частотные характеристики отклика систем (САУ)
- 40. Характеристики звеньев: усилительное безинерционное звено
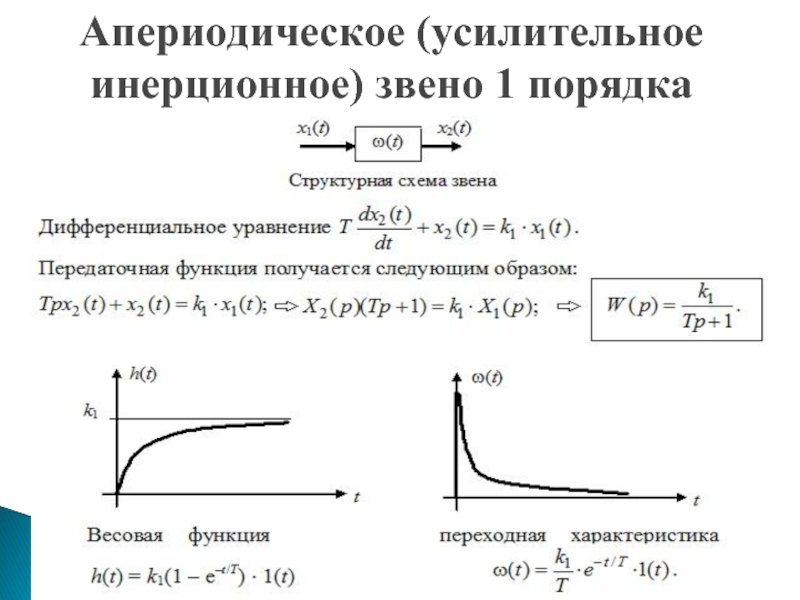
- 41. Апериодическое (усилительное инерционное) звено 1 порядка
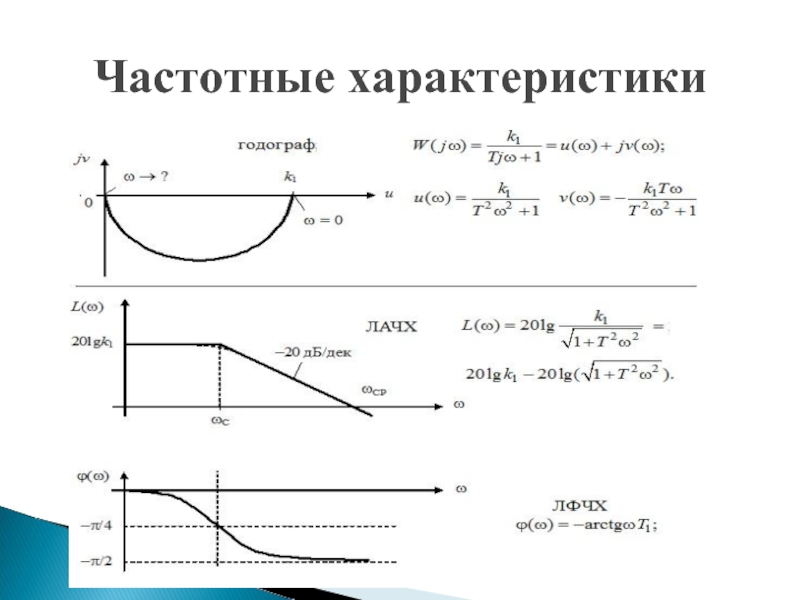
- 42. Частотные характеристики
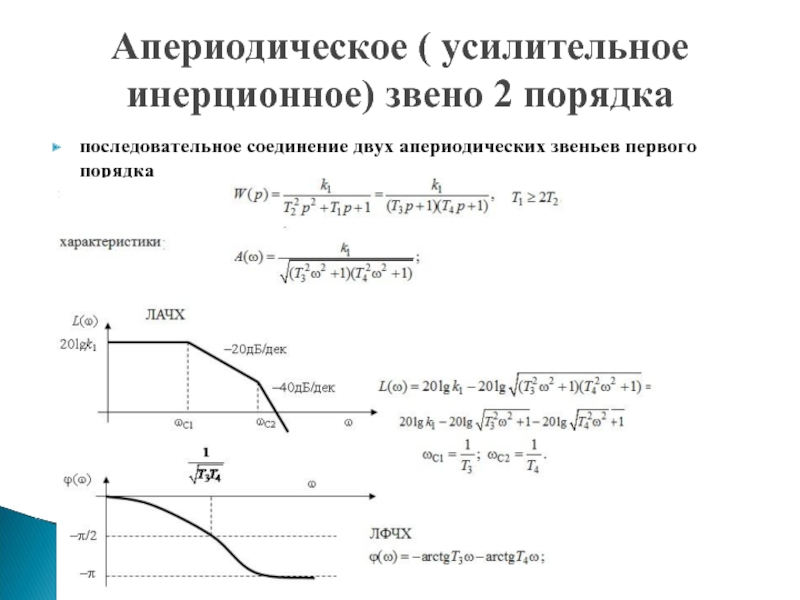
- 43. последовательное соединение двух апериодических звеньев первого порядка Апериодическое ( усилительное инерционное) звено 2 порядка
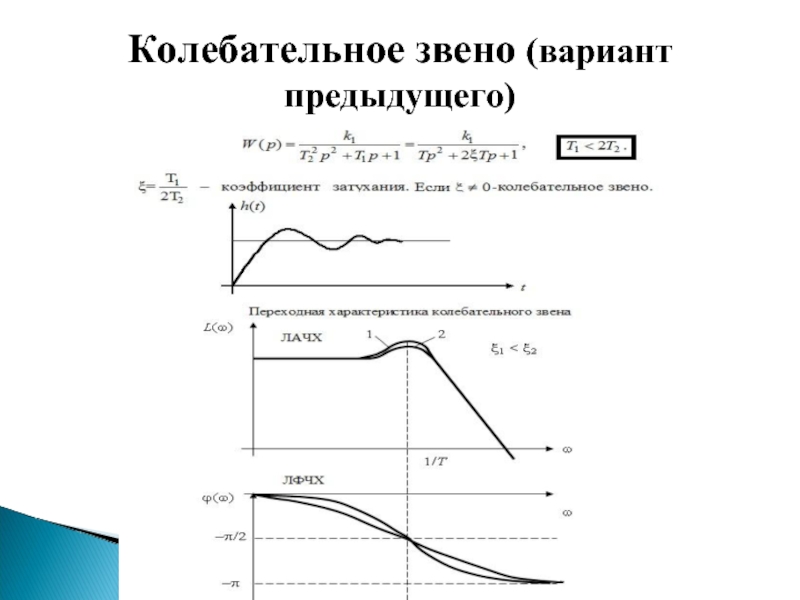
- 44. Колебательное звено (вариант предыдущего)
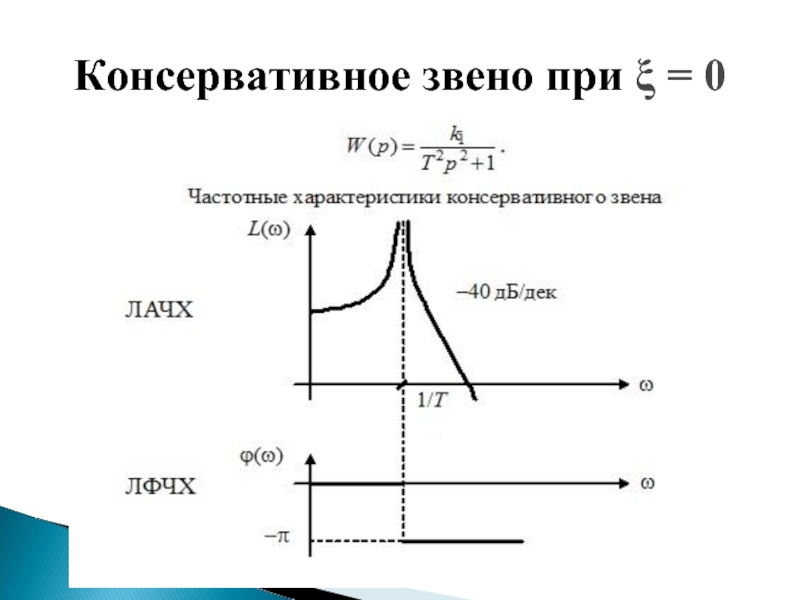
- 45. Консервативное звено при ξ = 0
- 46. Интегрирующее звено ∞
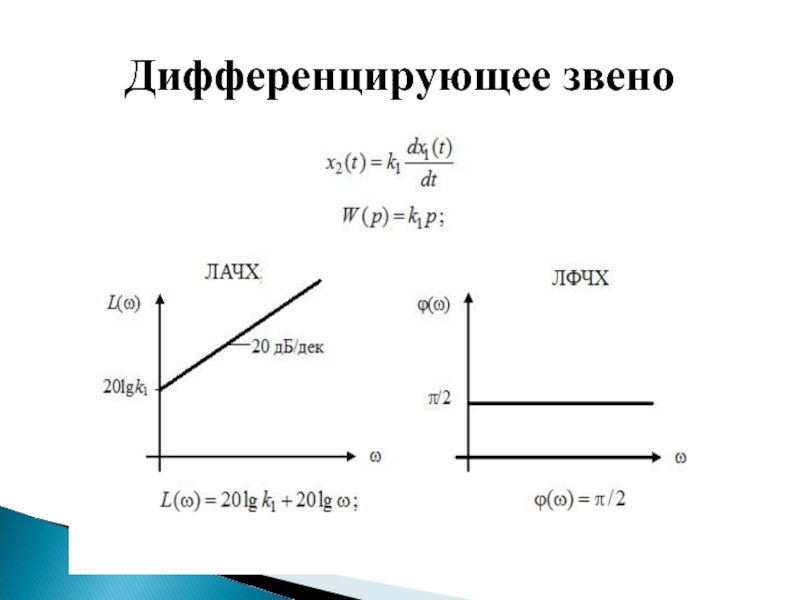
- 47. Дифференцирующее звено
- 48. Примеры использования звеньев на практике
- 49. Решение дифференциального уравнения Использование программных пакетов при расчете систем управления
- 50. LaplaceTransform[t*Sin[t],t,s] Ответ: (2 s)/(1+s^2)2
- 51. Использование преобразования Лапласа для построения передаточной функции
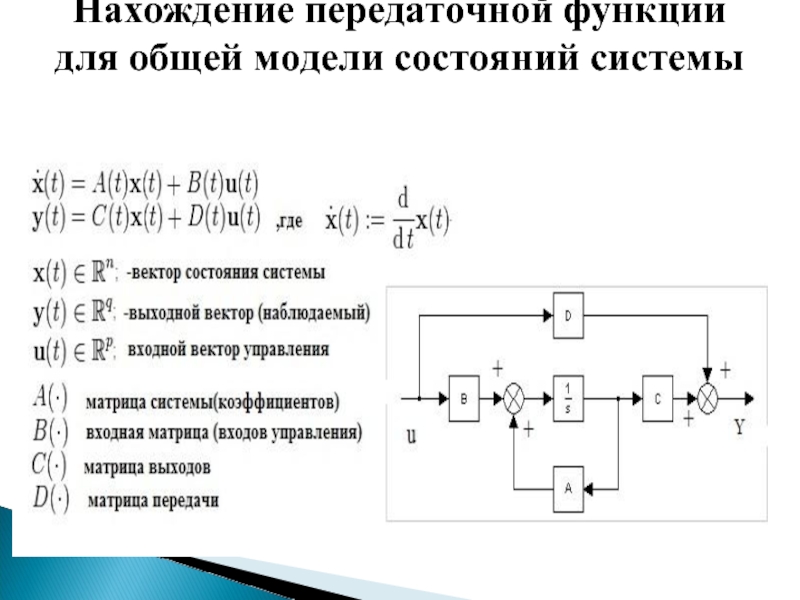
- 52. Нахождение передаточной функции для общей модели состояний системы
- 53. Одно уравнение x''[t]+A x'[t]+B x[t]=u[t] второго порядка
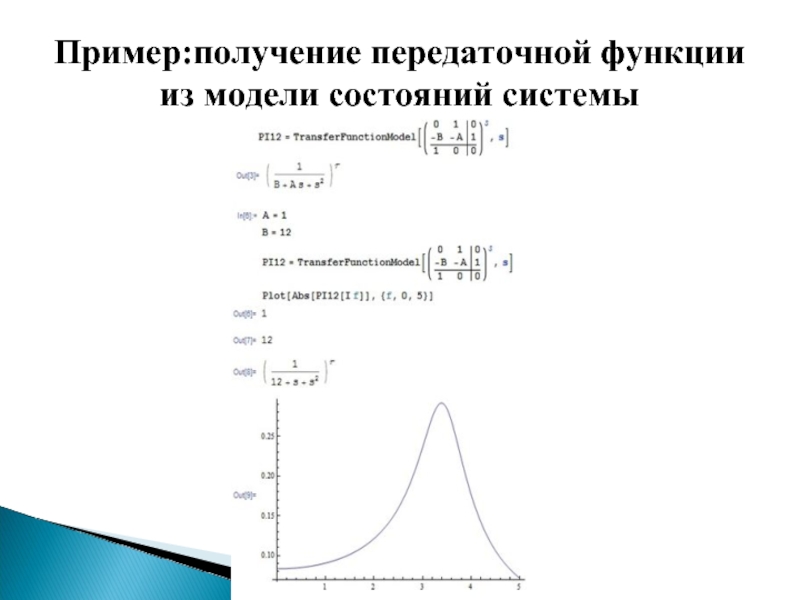
- 54. Пример:получение передаточной функции из модели состояний системы
- 55. Входное воздействие l(t)-UnitStep[t]
- 56. Входное воздействие δ(t)-DiracDelta[t]
- 57. Входное воздействие Sin[4 t]
- 58. один из способов судить об устойчивости замкнутой системы
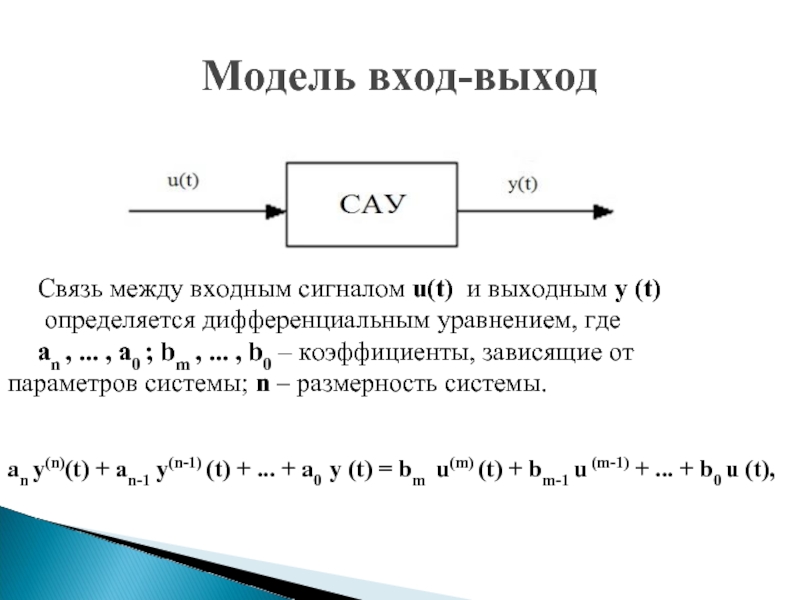
Слайд 19Модель вход-выход
an y(n)(t) + an-1 y(n-1) (t) + ... + a0
y (t) = bm u(m) (t) + bm-1 u (m-1) + ... + b0 u (t),
Связь между входным сигналом u(t) и выходным y (t)
определяется дифференциальным уравнением, где
an , ... , a0 ; bm , ... , b0 – коэффициенты, зависящие от параметров системы; n – размерность системы.
Слайд 43последовательное соединение двух апериодических звеньев первого порядка
Апериодическое ( усилительное инерционное) звено
2 порядка
Слайд 49Решение дифференциального уравнения
Использование программных пакетов при расчете систем управления
Слайд 50LaplaceTransform[t*Sin[t],t,s]
Ответ: (2 s)/(1+s^2)2
LaplaceTransform[DiracDelta[t],t,s]
Ответ : 1/s
LaplaceTransform[X''[t]-4*X'[t]+3*X[t],t,s]//TraditionalForm
Ответ
: s2 (Lt[X(t)](s))+3 (Lt[X(t)](s))-4 (s (Lt[X(t)](s))-X(0))-s X(0)-X¢(0)
Преобразование Лапласа
Слайд 53Одно уравнение x''[t]+A x'[t]+B x[t]=u[t] второго порядка эквивалентно системе из 2
уравнений первого порядка
x'[t]=z[t]
z'[t]=-A x'[t]- B x[t]+u[t]
Получение стандартной модели состояний системы в Математика 9
x'[t]=z[t]
z'[t]=-A x'[t]- B x[t]+u[t]
Получение стандартной модели состояний системы в Математика 9
Пример:получение стандартной модели из ДУ
Слайд 55
Входное воздействие l(t)-UnitStep[t] Выходная реакция-
(функция Хэвисайда) переходная функция
Нахождение переходной функции
Слайд 56
Входное воздействие δ(t)-DiracDelta[t] Выходная реакция-
импульсная функция
Нахождение импульсной переходной функции
Слайд 57
Входное воздействие Sin[4 t]
Выходная реакция-
гармонический отклик
гармонический отклик
Нахождение отклика системы на гармоническое воздействие
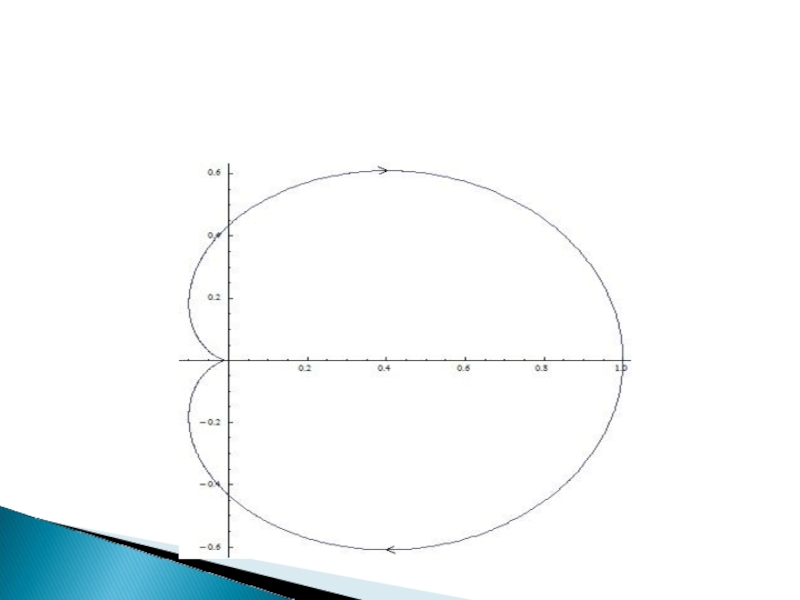
Слайд 58один из способов судить об устойчивости замкнутой системы управления по АФЧХ её разомкнутого состояния.
Если разомкнутая
система с передаточной функцией устойчива, замкнутая система является устойчивой, если АФЧХ разомкнутой системы не охватывает точку (−1; j0).
Устойчивость системы -Найквист
