- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Углы при параллельных прямых презентация
Содержание
- 1. Углы при параллельных прямых
- 2. Теорема, обратная данной. Теорема – это
- 3. Теорема, обратная данной. Данная теорема Обратная
- 4. Метод доказательства от противного. Алгоритм: Предполагаем
- 5. Теоремы об углах, образованных двумя параллельными прямыми
- 6. Теоремы об углах, образованных двумя параллельными прямыми
- 7. Теоремы об углах, образованных двумя параллельными прямыми
Слайд 1Теоремы об углах, образованных двумя параллельными прямыми и секущей.
Задачи для
Знать:
а) понятие теоремы, обратной данной;
б) алгоритм доказательства методом от противного;
в) теоремы об углах, образованных двумя параллельными прямыми и секущей.
2. Уметь применять эти знания при
решении задач.
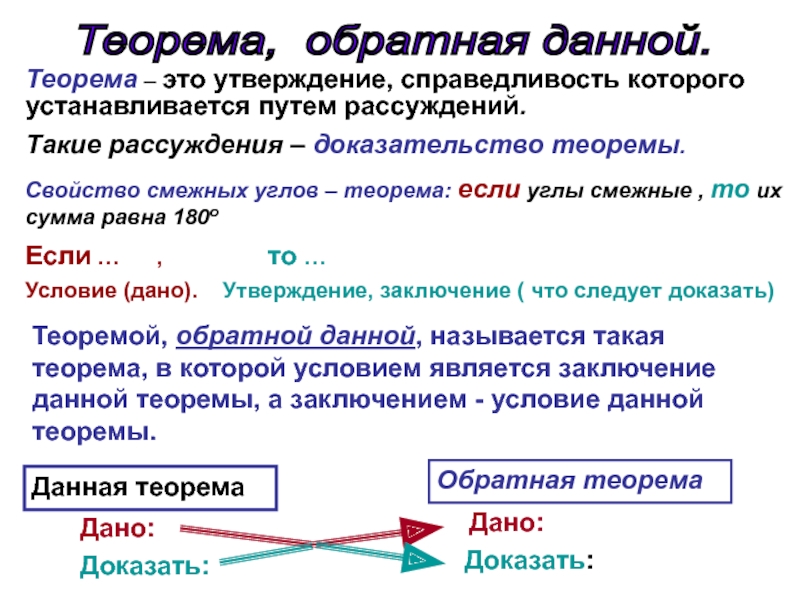
Слайд 2Теорема, обратная данной.
Теорема – это утверждение, справедливость которого устанавливается путем
Такие рассуждения – доказательство теоремы.
Свойство смежных углов – теорема: если углы смежные , то их сумма равна 180о
Если … , то …
Условие (дано). Утверждение, заключение ( что следует доказать)
Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением - условие данной теоремы.
Данная теорема
Обратная теорема
Дано:
Доказать:
Доказать:
Дано:
Слайд 3Теорема, обратная данной.
Данная теорема
Обратная теорема
Теорема. Если при пересечении двух прямых
Теорема. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
c
b
a
1
2
Дано: a; b; с – секущая; < 1 и < 2 – накрест лежащие; < 1 = < 2
Доказать: a b
c
b
a
1
2
Дано: a; b; с – секущая; < 1 и < 2 – накрест лежащие; a b
Доказать: < 1 = < 2
Слайд 4Метод доказательства от противного.
Алгоритм:
Предполагаем противоположное тому, что нужно доказать.
Выясняем, что
Находим противоречие с ранее изученными аксиомами, теоремами.
Делаем вывод: предположение неверно, а верно то, что нужно доказать.
Слайд 5Теоремы об углах, образованных двумя параллельными прямыми и секущей.
Теорема. Если
c
b
a
1
2
Дано: a; b; a b, с – секущая; < 1 и < 2 – накрест лежащие;
Доказать: < 1 = < 2
Доказательство
(методом от противного).
1) Предположим, что < 1 = < 2.
2) Тогда существует < 3 = < 2
< 3 и < 2 – накрест лежащие
m b, но по условию а b
3) m b; а b ; M a; M m. Противоречие с аксиомой параллельных прямых.
4) Вывод. Предположение неверно, а верно то, что надо доказать.
Значит, < 1 = < 2
m
3
M
Слайд 6Теоремы об углах, образованных двумя параллельными прямыми и секущей.
Теорема. Если
c
b
a
1
2
Дано: a; b; с – секущая; < 1 и < 2 – соответственные; a b
Доказать: < 1 = < 2
3
Доказательство.
< 1 = < 3 ( по теореме о накрест лежащих углах)
< 2 = < 3 ( вертикальные);
< 1 = < 2
Теорема. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180о.
b
a
1
2
3
c
Дано: a; b; с – секущая; < 1 и < 2 – односторонние; a b
Доказать: < 1 + < 2 = 180о
Доказательство.
< 1 = < 3 ( по теореме о накрест лежащих углах)
< 2 + < 3 = 180о (по свойству смежных углов);
< 1 + < 2 = 180о
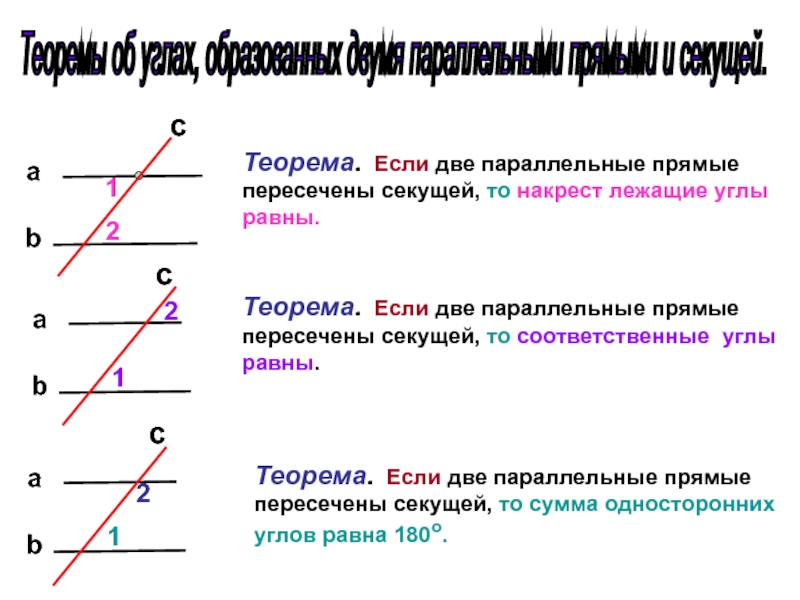
Слайд 7Теоремы об углах, образованных двумя параллельными прямыми и секущей.
c
b
a
1
2
Теорема. Если
c
b
a
1
2
b
a
1
2
c
Теорема. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180о.
Теорема. Если две параллельные прямые пересечены секущей, то соответственные углы равны.