: Феоктистова Юлия.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цилиндр, конус, шар презентация
Содержание
- 1. Цилиндр, конус, шар
- 2. Тело, ограниченное цилиндрической поверхностью и двумя кругами,
- 3. Площадь боковой поверхности цилиндра равна произведению длинны
- 4. Тело, ограниченное конической поверхностью и кругом, называется
- 5. Площадь боковой поверхности конуса равна произведению половины
- 6. Конус, который рассекли плоскостью, параллельной основанию, и убрали верхнюю часть, называется усечённым конусом. 6
- 7. Площадь боковой поверхности усечённого конуса равна произведению
- 8. Сферой называется поверхность, состоящая из всех точек
- 9. В прямоугольной системе координат уравнение сферы радиусом
- 10. Плоскость, имеющая со сферой только одну общую
- 11. Многогранник называется описанным около сферы, если сфера
Тело, ограниченное цилиндрической поверхностью и двумя кругами, называется
цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра. Круги называются основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими.
Прямая оо – ось цилиндра. Длинна образующей
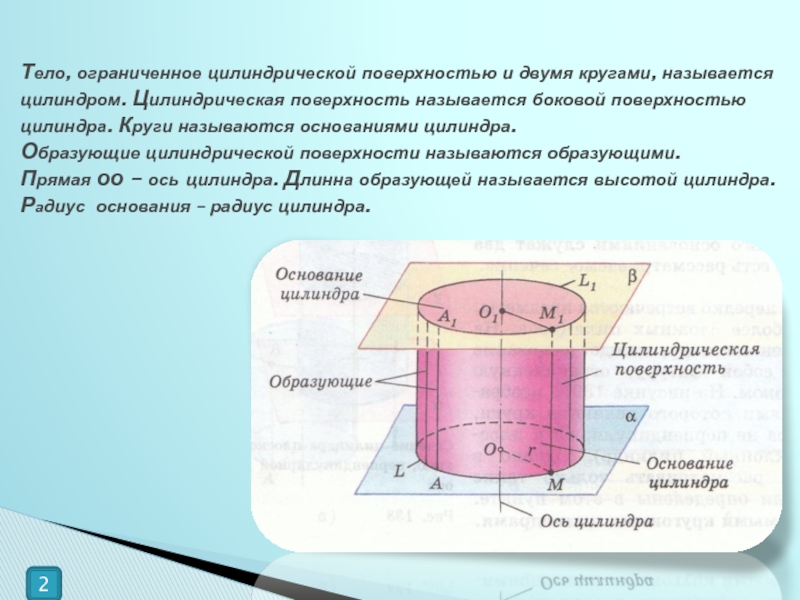
Слайд 2Тело, ограниченное цилиндрической поверхностью и двумя кругами, называется цилиндром. Цилиндрическая поверхность называется
боковой поверхностью цилиндра. Круги называются основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими.
Прямая оо – ось цилиндра. Длинна образующей называется высотой цилиндра.
Радиус основания – радиус цилиндра.
2
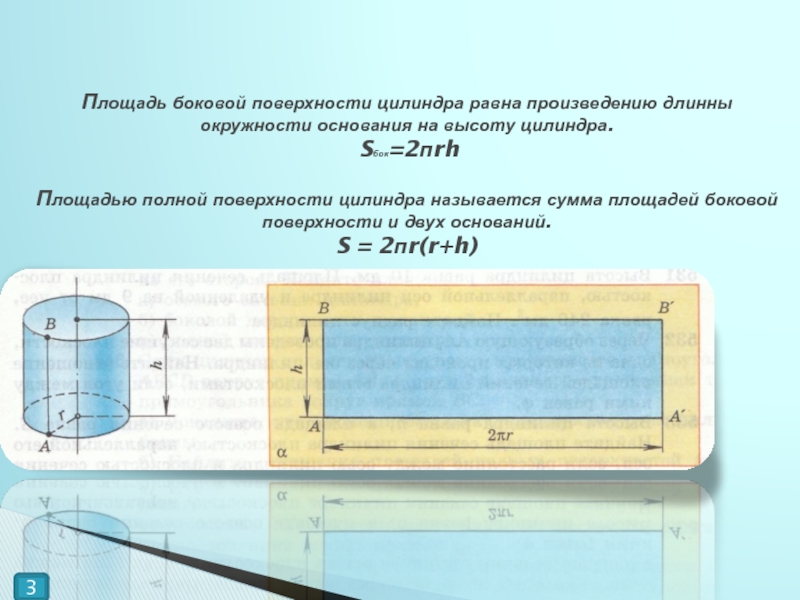
Слайд 3Площадь боковой поверхности цилиндра равна произведению длинны окружности основания на высоту
цилиндра.
Sбок=2пrh
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
S = 2пr(r+h)
3
Слайд 4Тело, ограниченное конической поверхностью и кругом, называется конусом. Коническая поверхность называется боковой
поверхностью. Круг – основание конуса. Р – вершина конуса. Образующие конической поверхности – образующие конуса. прямая ор – ось конуса. отрезок ор – высота конуса.
4
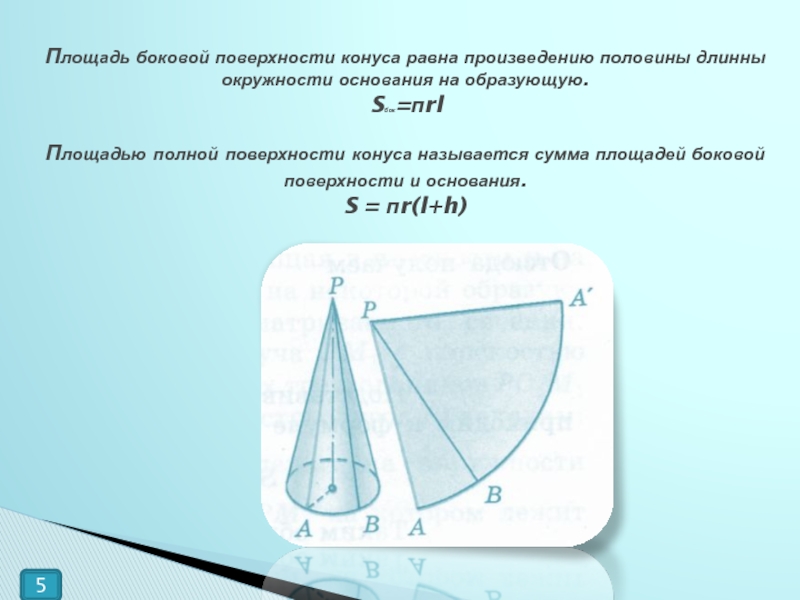
Слайд 5Площадь боковой поверхности конуса равна произведению половины длинны окружности основания на
образующую.
Sбок=пrl
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.
S = пr(l+h)
5
Слайд 6Конус, который рассекли плоскостью, параллельной основанию, и убрали верхнюю часть, называется
усечённым конусом.
6
Слайд 7Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований
на образующую.
Sбок=п(r1+r2)l
Площадью полной поверхности усечённого конуса называется сумма площадей боковой поверхности и оснований.
7
Слайд 8Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном
расстоянии от данной точки. О – центр сферы.
R – радиус сферы. тело, ограниченное сферой – шар.
8
Слайд 9В прямоугольной системе координат уравнение сферы радиусом r с центром с
имеет вид (x-x0)2 + (y-y0)2 + (z-z0)2 = r2
9
Слайд 10Плоскость, имеющая со сферой только одну общую точку , называется касательной
к сфере, а их общая точка – точкой касания.
Теорема 1.
радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема 2.
если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
10
Слайд 11Многогранник называется описанным около сферы, если сфера касается всех его граней. За
площадь сферы примем предел последовательности площадей поверхностей
описанных около сферы многогранников при стремлении к нулю наибольшего
размера каждой грани.
11
