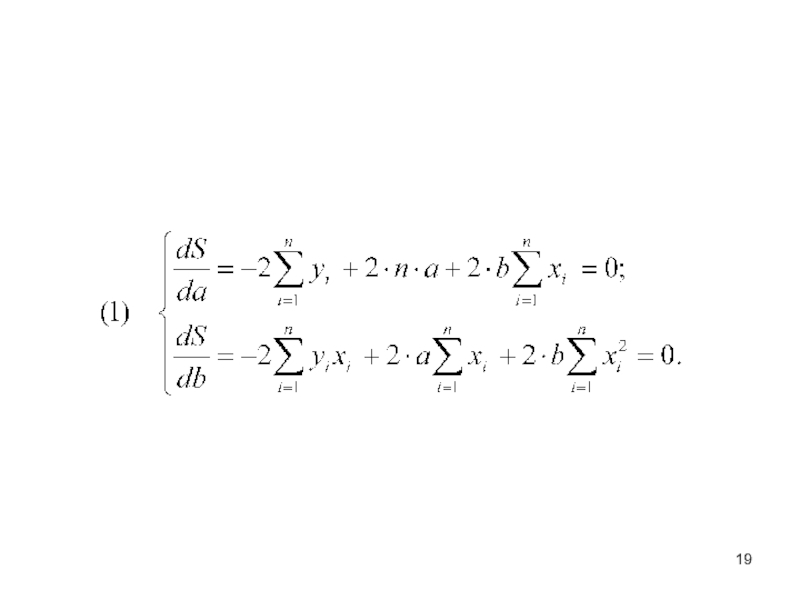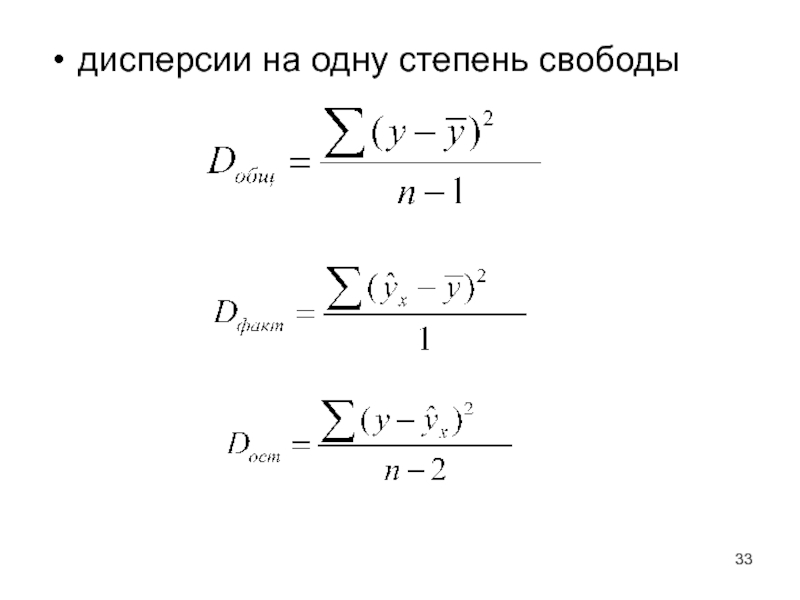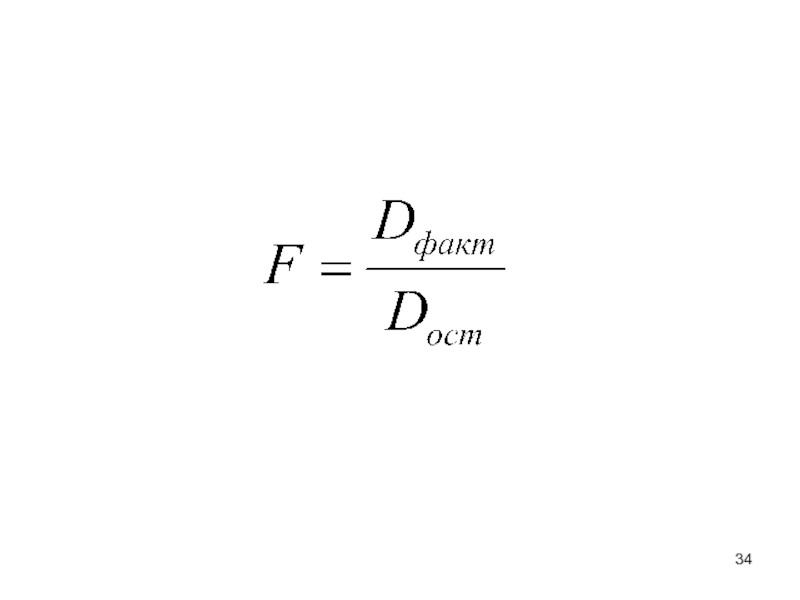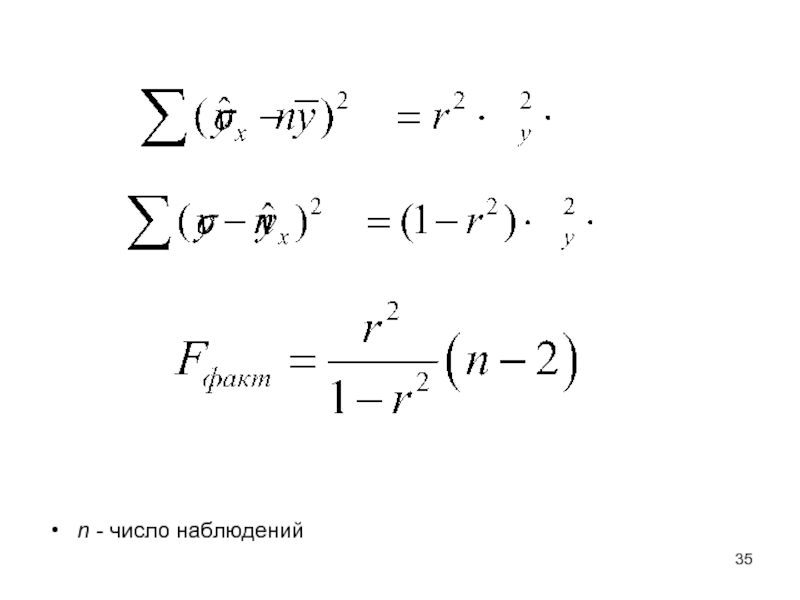доцент кафедры математики и моделирования (ауд.1602)
Литература:
Елисеева И.И. Эконометрика: учебник. - М.: Финансы и статистика, 2002.
Елисеева И.И. С.В. Курышева, Н.М. Гордеенко и др. Практикум по эконометрике: учеб. пособие. - М.: Финансы и статистика, 2001.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2002.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: учебник. – М.: Дело, 2000.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Центральные проблемы эконометрики презентация
Содержание
- 1. Центральные проблемы эконометрики
- 2. Опр. эконометрика — это наука,
- 4. Эконометрическое исследование включает решение следующих проблем:
- 5. этапы эконометрического исследования:
- 6. проблема точности связана
- 7. Регрессия в эконометрических исследованиях.
- 8. Простая регрессия представляет собой регрессию между двумя
- 9. Множественная регрессия представляет собой регрессию результативного признака
- 10. ПРИМЕР. Так, если зависимость спроса
- 11. В парной регрессии выбор вида математической функции
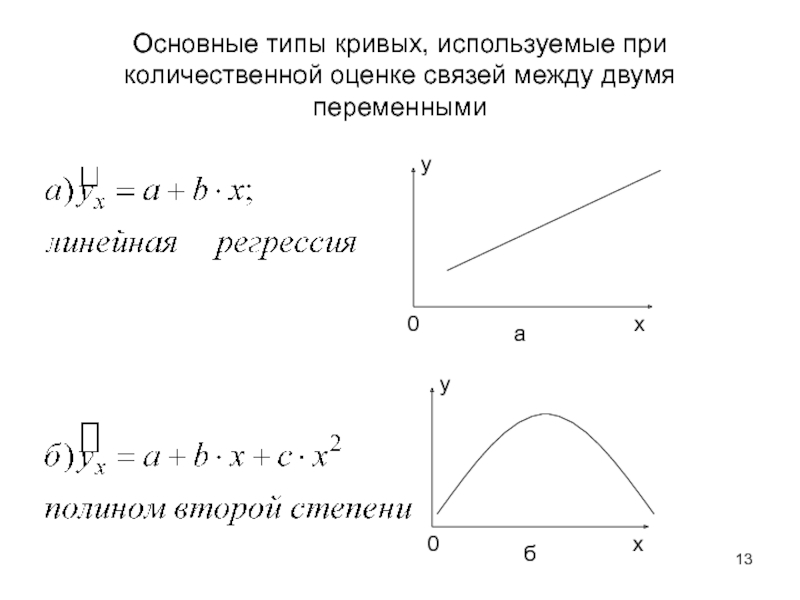
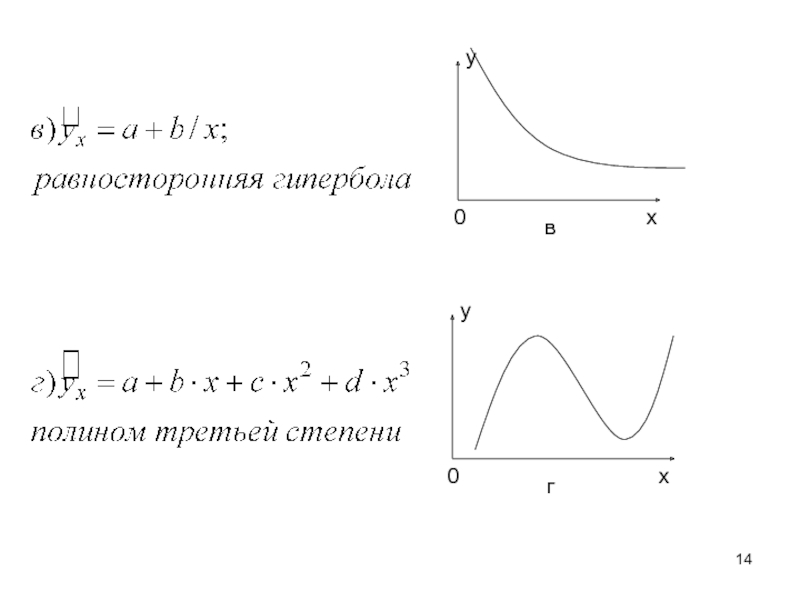
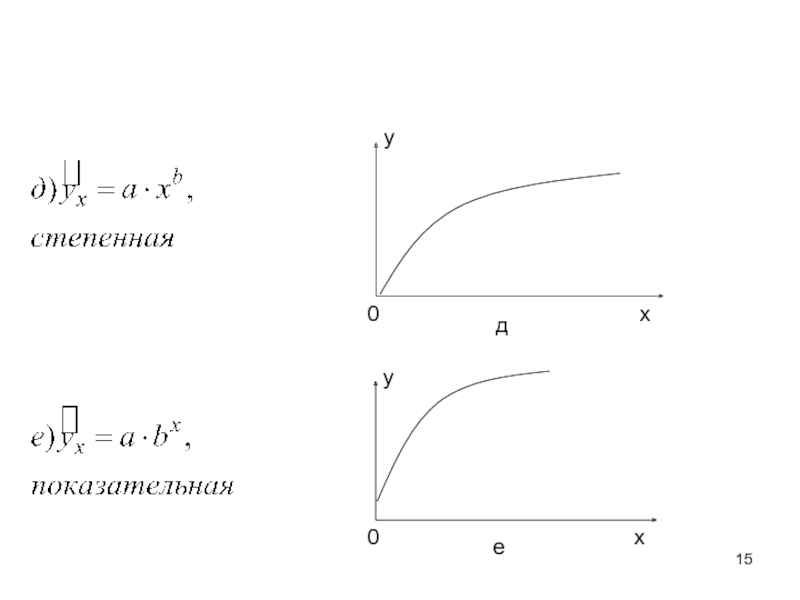
- 13. Основные типы кривых, используемые при количественной оценке связей между двумя переменными
- 16. Классический подход к оцениванию
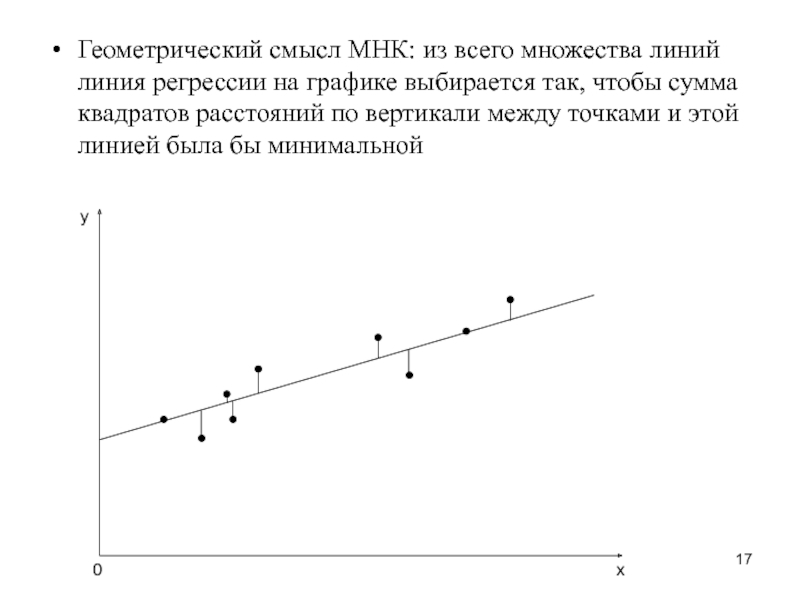
- 17. Геометрический смысл МНК: из всего множества линий
- 18. Обозначим
- 20. для оценки параметров а и b получим следующую систему нормальных уравнений
- 21. Формулы расчета параметров a и b:
- 22. Линейный коэффициент корреляции должен находится в границах:
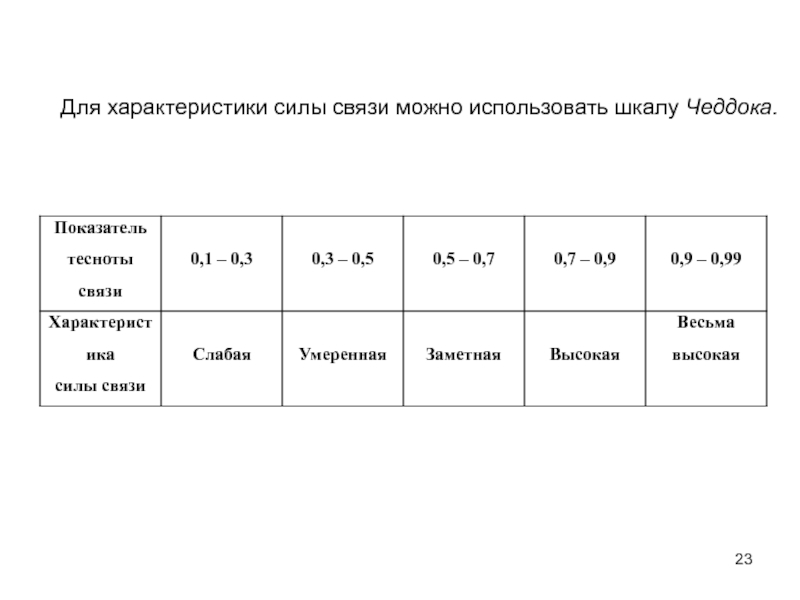
- 23. Для характеристики силы связи можно использовать шкалу Чеддока.
- 24. Коэффициент детерминации характеризует
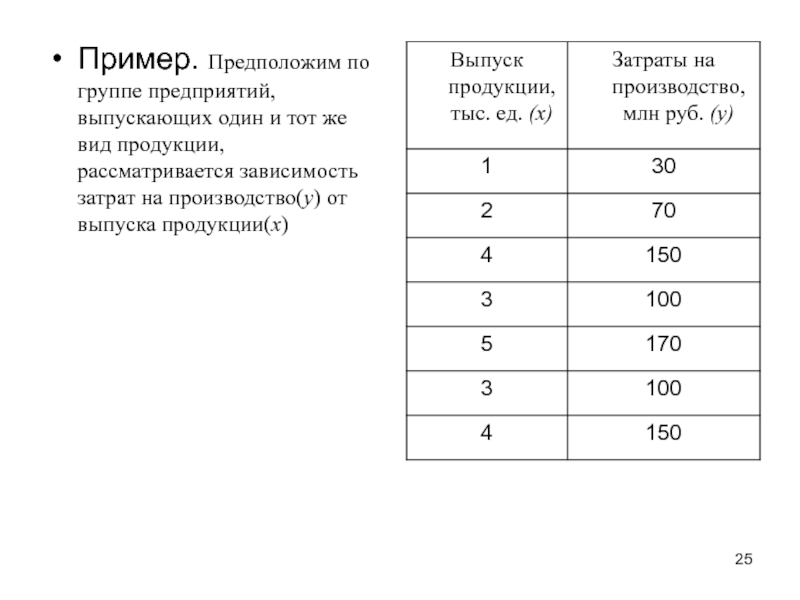
- 25. Пример. Предположим по группе предприятий, выпускающих один
- 26. Система нормальных уравнений будет иметь вид
- 27. Вывод: чем больше
- 28. Оценка существенности уравнения линейной регрессии.
- 29. F критерий Фишера - оценивает качество
- 30. Расчету F-критерия предшествует анализ дисперсии. Центральное место
- 31. Любая сумма квадратов отклонений связана с числом
- 32. Число степеней свободы остаточной суммы квадратов при
- 33. дисперсии на одну степень свободы
- 36. Значение F-критерия признается достоверным, если
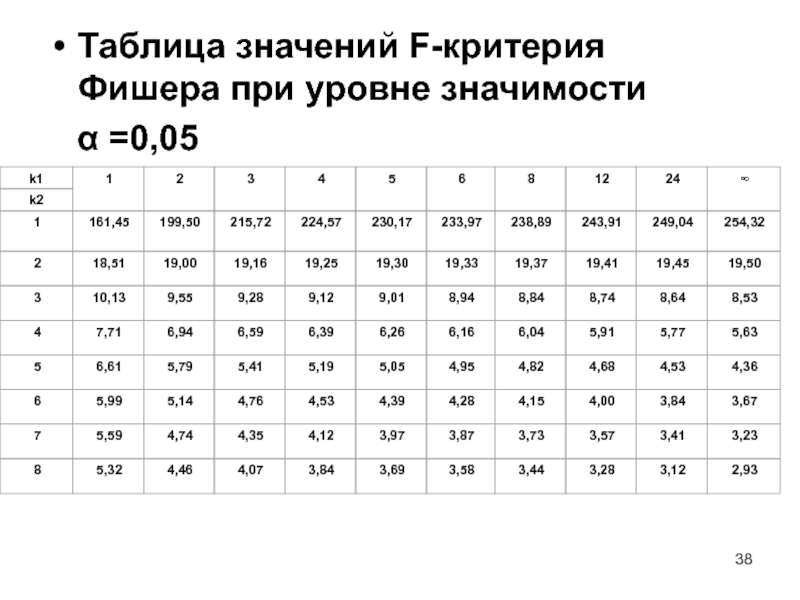
- 38. Таблица значений F-критерия Фишера при уровне значимости
- 39. ПРИМЕР Дисперсионный анализ результатов регрессии
Опр. эконометрика — это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.
Слайд 2
Опр. эконометрика — это наука, которая дает количественное выражение взаимосвязей экономических
явлений и процессов.
Слайд 4Эконометрическое исследование включает решение следующих проблем:
• качественный анализ связей экономических переменных
— выделение зависимых (у) и независимых переменных (х);
• подбор данных;
• спецификация формы связи между у и х,
• оценка параметров модели;
• введение фиктивных переменных;
• выявление тренда, циклической и случайной компонент; и др.
• подбор данных;
• спецификация формы связи между у и х,
• оценка параметров модели;
• введение фиктивных переменных;
• выявление тренда, циклической и случайной компонент; и др.
Слайд 6 проблема точности связана с:
определением понятия экономической величины;
разработкой правил и методов измерений
выявлением условий сравнимости экономических величин (показателей);
разработкой принципов конструирования измерителей и измерений;
основанием выбора типа шкал при конструировании измерителя;
выявлением условий сравнимости экономических величин (показателей);
разработкой принципов конструирования измерителей и измерений;
основанием выбора типа шкал при конструировании измерителя;
Слайд 8Простая регрессия представляет собой регрессию между двумя переменными — у и
х, т. е. модель вида:
где:
у – зависимая переменная (результативный признак);
х – независимая, или объясняющая, переменная (признак-фактор).
Слайд 9Множественная регрессия представляет собой регрессию результативного признака с двумя и большим
числом факторов, т. е. модель вида:
Слайд 11В парной регрессии выбор вида математической функции
может быть осуществлен тремя
методами:
• графическим;
• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
• экспериментальным.
• графическим;
• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
• экспериментальным.
Слайд 16 Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших
квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака (уi ) от расчетных (теоретических) минимальна:
Слайд 17Геометрический смысл МНК: из всего множества линий линия регрессии на графике
выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной
Слайд 21Формулы расчета параметров a и b:
b - коэффициент регрессии. Его
величина показывает среднее изменение результата с изменением фактора на одну единицу.
Слайд 22Линейный коэффициент корреляции должен находится в границах:
Линейный коэффициент корреляции является
показателем
тесноты связи:
тесноты связи:
Слайд 24
Коэффициент детерминации характеризует долю дисперсии результативного признака :
Величина 1- r 2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
Слайд 25Пример. Предположим по группе предприятий, выпускающих один и тот же вид
продукции, рассматривается зависимость затрат на производство(у) от выпуска продукции(х)
Слайд 26Система нормальных уравнений будет иметь вид
а = -5,798, b= 36,8443,
r 2
= 0,982.
уравнение регрессии:
уравнение регрессии:
Слайд 27
Вывод:
чем больше доля объясненной вариации, тем соответственно меньше
роль прочих факторов, и линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака.
Слайд 29
F критерий Фишера - оценивает качество уравнения регрессии - состоит в
проверке гипотезы Н0 (о том, что коэффициент регрессии равен нулю, т.е. b = 0, т.е. фактор х не оказывает влияния на результат у ).
Слайд 30Расчету F-критерия предшествует анализ дисперсии.
Центральное место в нем занимает разложение общей
суммы квадратов отклонений на две части «объясненную» и «необъясненную» .
Общая факторная остаточная
(регрессионная) (необъясненная)
Общая факторная остаточная
(регрессионная) (необъясненная)
Слайд 31Любая сумма квадратов отклонений связана с числом степеней свободы – df
(degrees of freedom), т.е. с числом свободы независимого варьирования признака.
Слайд 32Число степеней свободы остаточной суммы квадратов при линейной парной регрессии составляет
n - 2 ,
общей суммы квадратов – n -1 ,
для факторной суммы квадратов – 1,
Имеем равенство:
n – 1 = 1+ (n – 2).
общей суммы квадратов – n -1 ,
для факторной суммы квадратов – 1,
Имеем равенство:
n – 1 = 1+ (n – 2).
Слайд 36
Значение F-критерия признается достоверным, если оно больше табличного. В этом случае
гипотеза H0 отклоняется.
