Дисциплина Математика 2
Лекция 10
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрическая система функций. Ряды Фурье. Разложение функций в ряд Фурье презентация
Содержание
- 1. Тригонометрическая система функций. Ряды Фурье. Разложение функций в ряд Фурье
- 2. План лекции 1. Ряды Фурье: основные понятия.
- 3. Если функция y=f(x) интегрируема на отрезке [-П,П]
- 4. Доказательство: Для определения коэффициентов разложения будем
- 6. Для определения коэффициентов an и bn последовательно
- 8. Для функции f(x), интегрируемой на отрезке
- 9. Для определения сходимости ряда Фурье вводится понятие
- 10. Если ряд Фурье сходится к функции f(x)
- 11. Теорема Пусть функция y=f(x) непрерывна
- 12. Ряд Фурье функции f(x) сходится на всей
- 13. В каждой точке разрыва функции х /
- 14. На концах отрезка [-П,П] сумма ряда равна 3
- 15. Для любой точки х, не принадлежащей отрезку
- 16. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ
- 17. Пусть функция f(x) определена и является нечетной на отрезке [-П,П]: Найдем коэффициенты разложения:
- 18. В первом интеграле делаем замену:
- 19. Тогда
- 21. Таким образом, нечетная на отрезке [-П,П] функция
- 22. Пусть функция f(x) определена и является четной на отрезке [-П,П]: Найдем коэффициенты разложения:
- 23. В первом интеграле делаем замену:
- 24. Тогда
- 26. Таким образом, четная на отрезке [-П,П] функция
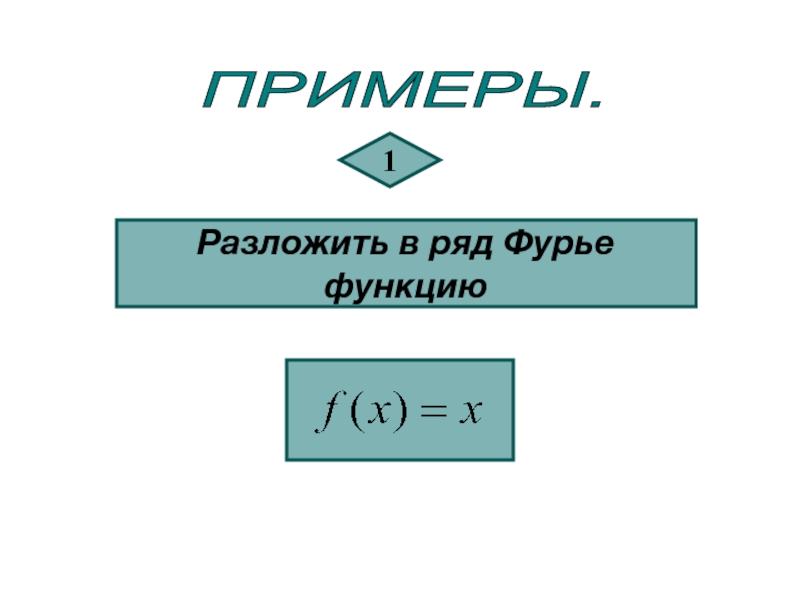
- 27. ПРИМЕРЫ. 1 Разложить в ряд Фурье функцию
- 28. РЕШЕНИЕ. Данная функция удовлетворяет всем условиям
- 29. Интеграл берем по частям:
- 30. Тогда ряд Фурье для данной функции будет иметь вид:
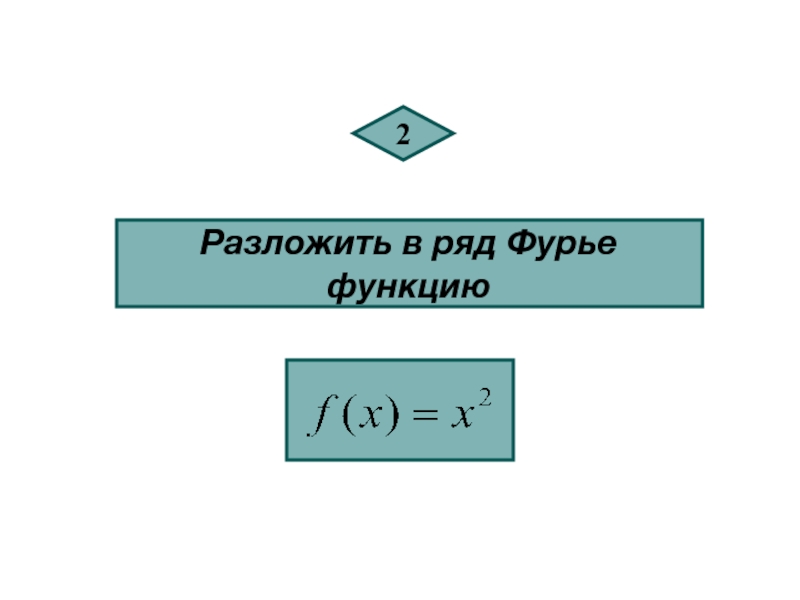
- 31. 2 Разложить в ряд Фурье функцию
- 32. РЕШЕНИЕ. Данная функция удовлетворяет всем условиям
- 33. При n=1, 2, 3…: Интеграл берем по частям:
- 34. Оставшийся интеграл снова берем по частям:
- 35. Тогда ряд Фурье для данной функции будет иметь вид:
- 36. Задания на СРС Преобразование Фурье Разложите в
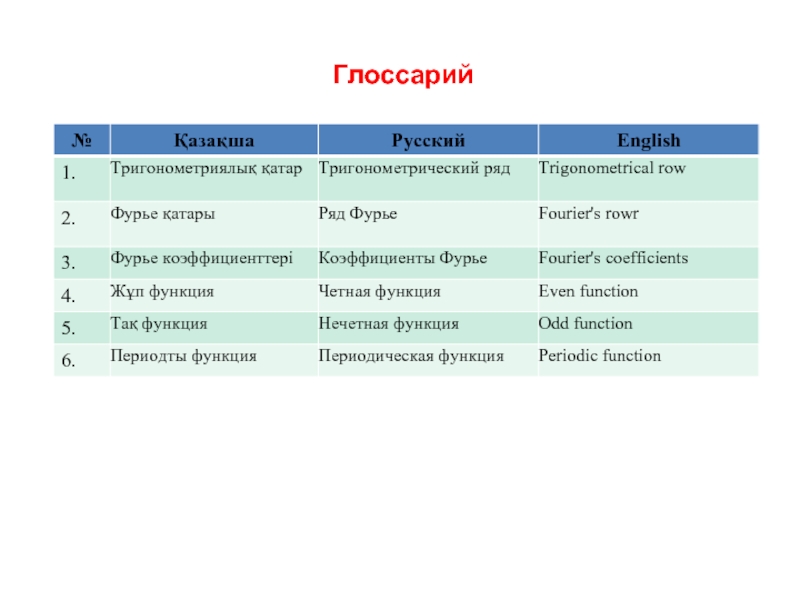
- 37. Глоссарий
- 38. Литература Основная: 1.Пискунов Н.С. Дифференциальное и
Слайд 1Лектор Буганова С.Н.
Тригонометрическая система функций. Ряды Фурье. Разложение функций в ряд
Слайд 2План лекции
1. Ряды Фурье: основные понятия.
2. Ряды Фурье для четных и
3. Примеры.
Слайд 3Если функция y=f(x) интегрируема на отрезке [-П,П] и разлагается в тригонометрический
который можно интегрировать почленно при умножении его на ограниченную функцию, то это разложение единственно.
1
РЯД ФУРЬЕ
Для тригонометрического ряда, как и для степенного ряда, можно установить условия разложения функций.
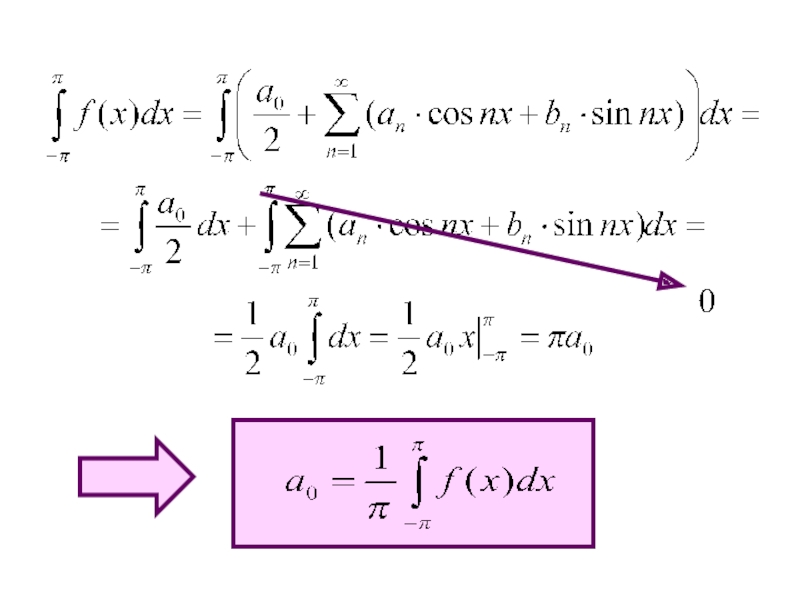
Слайд 4Доказательство:
Для определения коэффициентов разложения будем использовать ортогональность системы тригонометрических функций.
Проинтегрируем
Все интегралы, кроме интеграла от первого слагаемого, обращаются в нуль.
Слайд 6Для определения коэффициентов an и bn последовательно умножим обе части (1)
Все интегралы в правой части, кроме содержащих квадраты этих функций, равны нулю.
Полученные формулы будут определять единственным образом коэффициенты разложения функции в ряд.
Слайд 8Для функции f(x), интегрируемой на отрезке
[-П,П] числа a0, an, bn
коэффициентами ряда Фурье, а ряд (1) с
этими коэффициентами называется
рядом Фурье функции f(x).
Слайд 9Для определения сходимости ряда Фурье вводится понятие периодического продолжения функции, заданной
[-Т,Т].
Функция F(x), определенная на всей числовой
оси и периодическая с периодом Т, является
периодическим продолжением функции f(x),
если F(x)=f(x) на отрезке [-П,П].
Слайд 10Если ряд Фурье сходится к функции f(x) на
отрезке [-П,П], то
числовой прямой к ее периодическому
продолжению.
Слайд 11Теорема
Пусть функция y=f(x) непрерывна вместе со своей производной на отрезке
Тогда
Слайд 12Ряд Фурье функции f(x) сходится на всей
числовой прямой, и в
непрерывности f(x) в интервале (-П,П]
сумма ряда равна значению f(x)
в этой точке.
1
Слайд 13В каждой точке разрыва функции х /
сумма ряда равна полусумме
односторонних пределов f(x) в этой точке:
2
Слайд 15Для любой точки х, не принадлежащей
отрезку [-П,П] утверждения 1-3
справедливы для периодического
продолжения F(x) функции f(x).
4
Слайд 16 РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
Для четных и
Слайд 17Пусть функция f(x) определена и является нечетной на отрезке [-П,П]:
Найдем коэффициенты
Слайд 21Таким образом, нечетная на отрезке
[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим
Слайд 22Пусть функция f(x) определена и является четной на отрезке [-П,П]:
Найдем коэффициенты
Слайд 26Таким образом, четная на отрезке
[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим
Слайд 28РЕШЕНИЕ.
Данная функция удовлетворяет всем условиям теоремы о разложении функции в
Она является нечетной на отрезке [-П,П], поэтому
Слайд 32РЕШЕНИЕ.
Данная функция удовлетворяет всем условиям теоремы о разложении функции в
Она является четной на отрезке [-П,П], поэтому
При n=0:
Слайд 36Задания на СРС
Преобразование Фурье Разложите в ряд элементарные функции [ 1,3].
Решение
Задания на СРСП
1. Интегралы (преобразования) Фурье
[1, 3].
Слайд 38Литература
Основная:
1.Пискунов Н.С. Дифференциальное и интегральное исчисления. М. 2006.
2. Сборник индивидуальных заданий
Учеб. пособие в 4 частях / Под общей редакцией А.П. Рябушко. - Мн.: Выш. шк., 2011, часть 3.
Дополнительная:
3. Власова Е.А. Ряды: учебник для вузов /Под ред. Зарубина В.С., Крищенко А.П.. – 3-е изд. –М.:МГТУ им. Н.Э.Баумана, 2006. – 616 с.


![Если функция y=f(x) интегрируема на отрезке [-П,П] и разлагается в тригонометрический рядкоторый можно интегрировать почленно](/img/tmb/1/80073/660b95b71438a8ac0354708195201c00-800x.jpg)
![Доказательство: Для определения коэффициентов разложения будем использовать ортогональность системы тригонометрических функций.Проинтегрируем (1) на отрезке [-П,П].](/img/tmb/1/80073/607a63c1a7018be913f4bd2dff68fafb-800x.jpg)

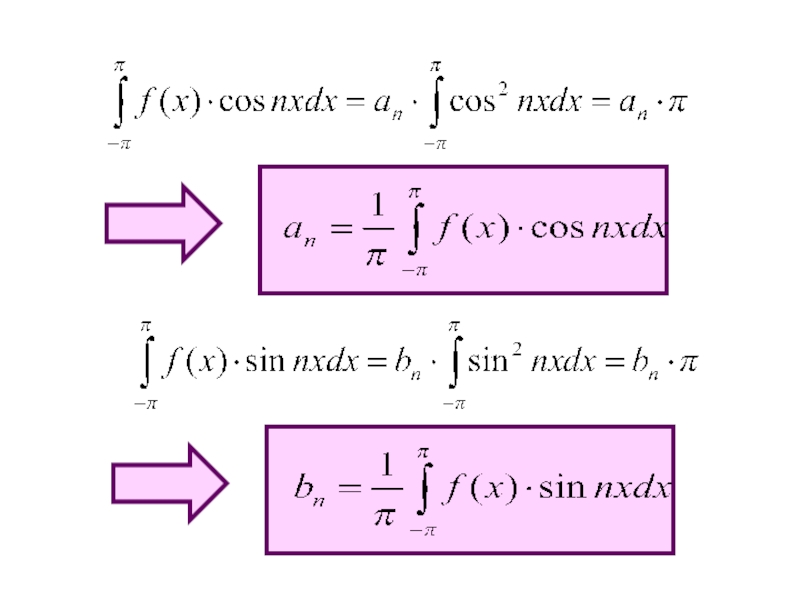
![Для функции f(x), интегрируемой на отрезке [-П,П] числа a0, an, bn называются коэффициентами ряда Фурье,](/img/tmb/1/80073/0d355f60a1eb4b0d3d00cf7675d64e19-800x.jpg)
![Для определения сходимости ряда Фурье вводится понятие периодического продолжения функции, заданной на отрезке [-Т,Т].Функция F(x),](/img/tmb/1/80073/e3754752224e3cc00ea0487bdb4a366b-800x.jpg)
![Если ряд Фурье сходится к функции f(x) на отрезке [-П,П], то он сходится на всей](/img/tmb/1/80073/9672a1370de210334c4fbc8717753a46-800x.jpg)
![Теорема Пусть функция y=f(x) непрерывна вместе со своей производной на отрезке [-П,П], или они имеют](/img/tmb/1/80073/0cdeed55114b40858c7dbcf30df4cf13-800x.jpg)


![На концах отрезка [-П,П]сумма ряда равна3](/img/tmb/1/80073/740aed3d057d434ec8affee6280d4773-800x.jpg)
![Для любой точки х, не принадлежащейотрезку [-П,П] утверждения 1-3справедливы для периодического продолжения F(x) функции f(x).4](/img/tmb/1/80073/f91c97e4ed293c5b920bea11cf332498-800x.jpg)

![Пусть функция f(x) определена и является нечетной на отрезке [-П,П]:Найдем коэффициенты разложения:](/img/tmb/1/80073/85ebacc5c9a54e37b0ec46a03f71a6bb-800x.jpg)

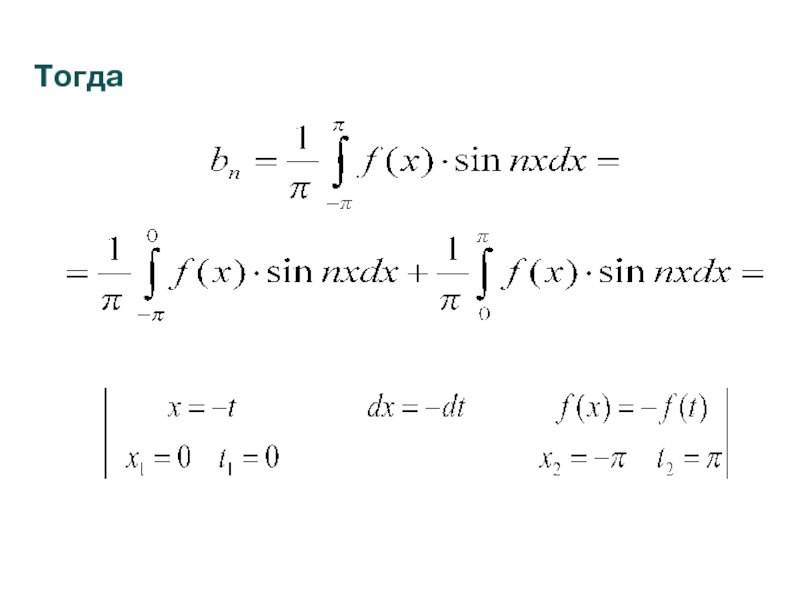
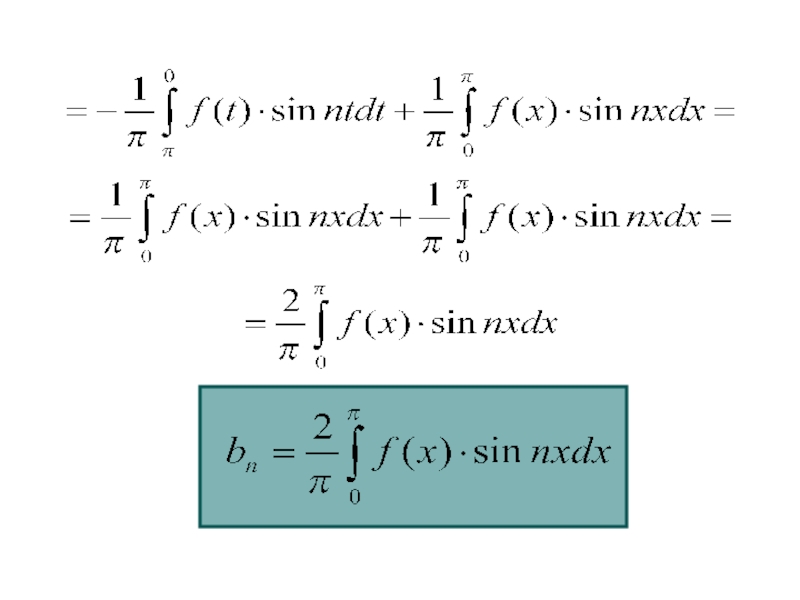
![Таким образом, нечетная на отрезке[-П,П] функция f(x) будетразлагаться в ряд Фурьеследующим образом:](/img/tmb/1/80073/42e3cc29ed4e0f4136e16348f945038b-800x.jpg)
![Пусть функция f(x) определена и является четной на отрезке [-П,П]:Найдем коэффициенты разложения:](/img/tmb/1/80073/b8e57f321f53379637f7845b0a663925-800x.jpg)

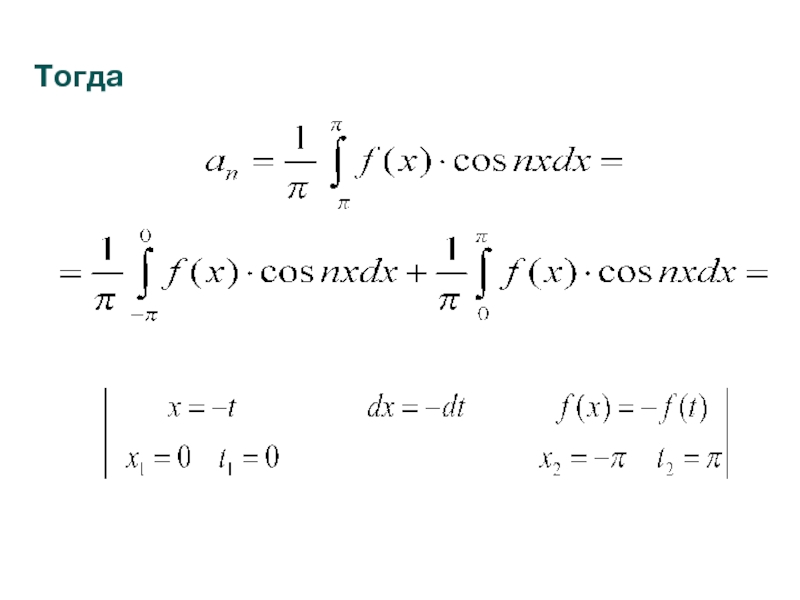
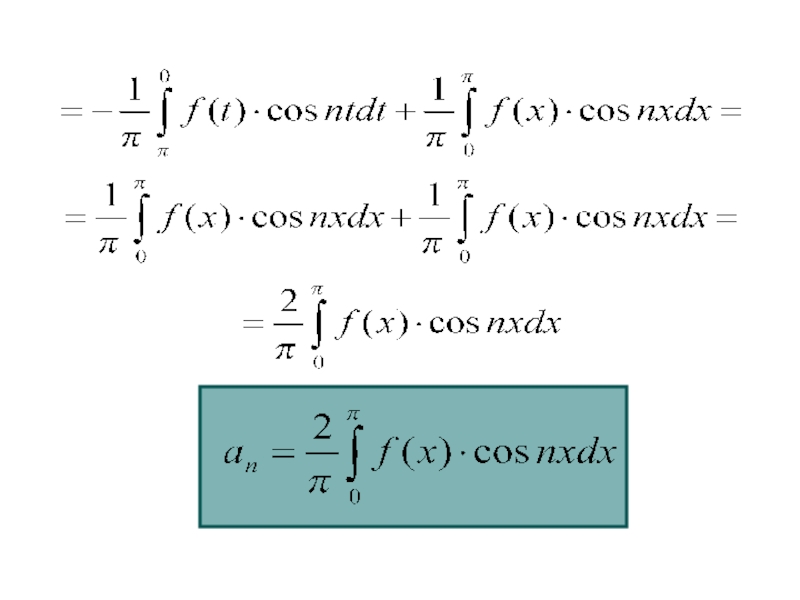
![Таким образом, четная на отрезке[-П,П] функция f(x) будетразлагаться в ряд Фурьеследующим образом:](/img/tmb/1/80073/54d944275c8b9eae4fadc6c6c7760dd3-800x.jpg)







![Задания на СРСПреобразование Фурье Разложите в ряд элементарные функции [ 1,3].Решение задач по теме [](/img/tmb/1/80073/94cf45490720b1511121a846de44fdc8-800x.jpg)