- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники. Основные признаки и свойства треугольников презентация
Содержание
- 1. Треугольники. Основные признаки и свойства треугольников
- 2. Цель работы: обобщить и систематизировать знания по
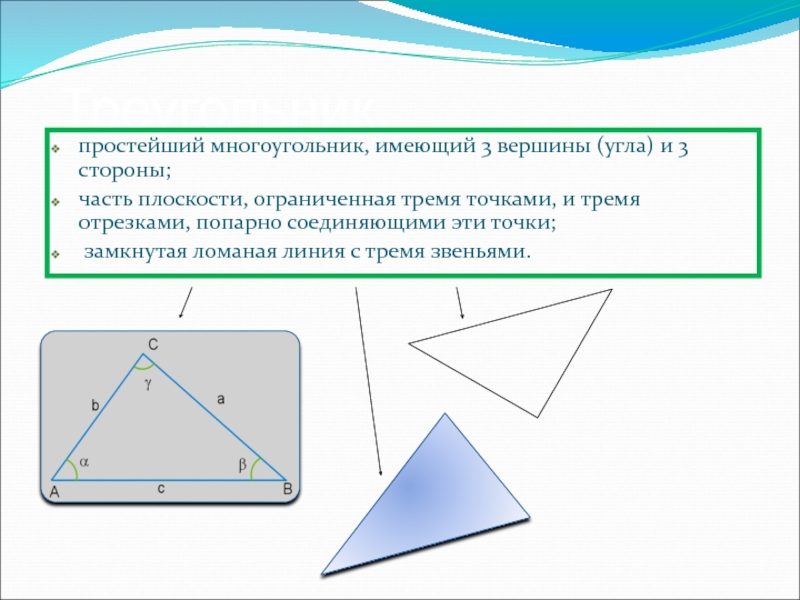
- 3. Треугольник простейший многоугольник, имеющий 3 вершины (угла)
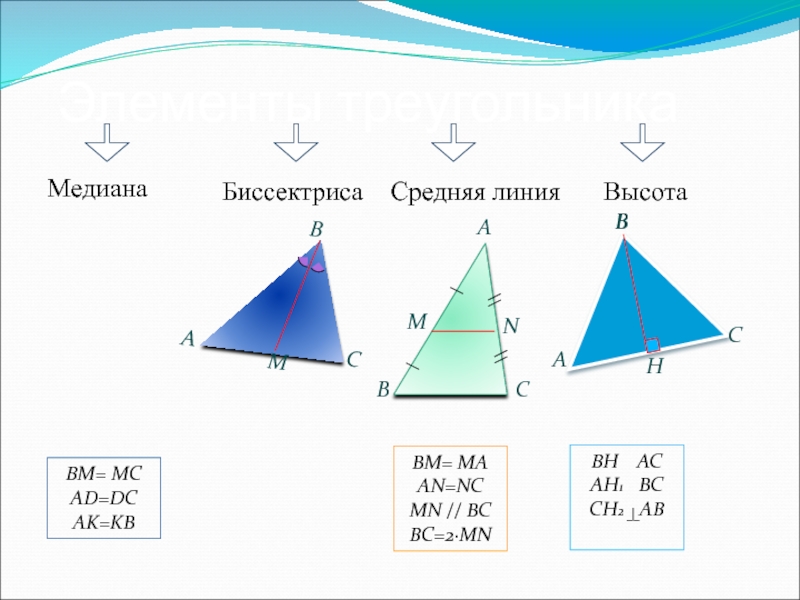
- 4. Элементы треугольника
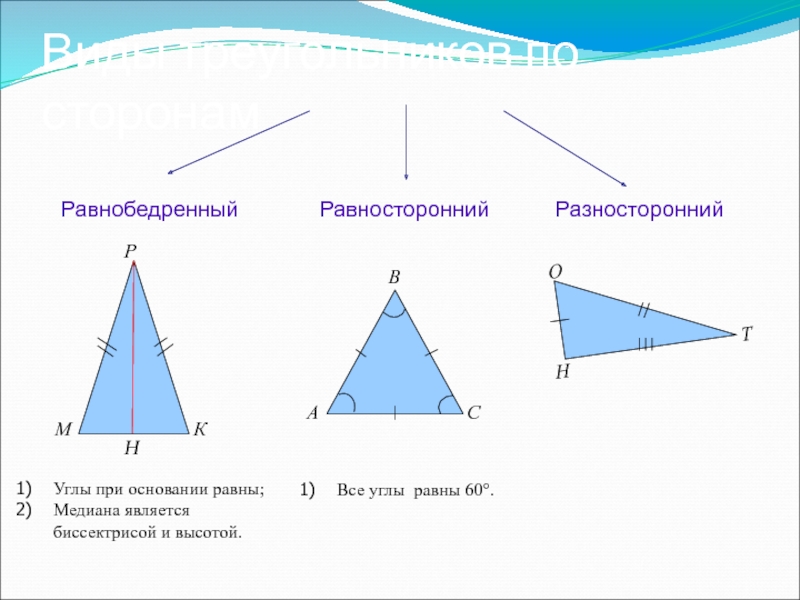
- 5. Виды треугольников по сторонам Равносторонний Равнобедренный Разносторонний
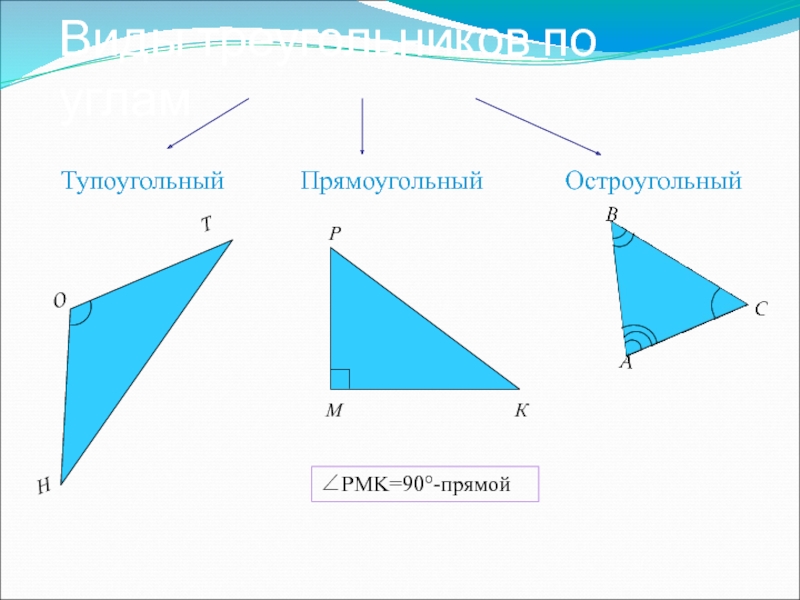
- 6. Виды треугольников по углам Прямоугольный Тупоугольный Н О Т Остроугольный ∠PMK=90°-прямой
- 7. Равенство треугольников Признаки равенства треугольников: 2.
- 8. Подобие треугольников Признаки подобия треугольников: 1.
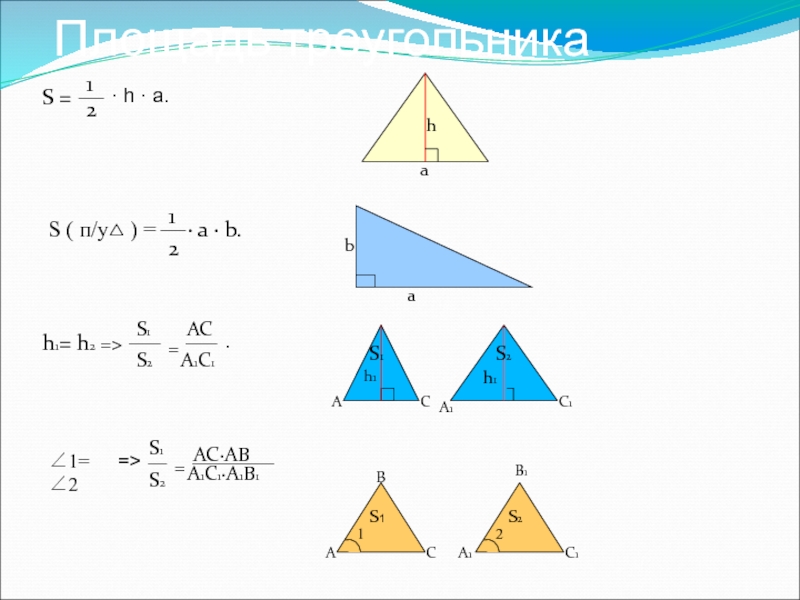
- 9. Площадь треугольника 2 1 S = · h · a.
- 10. Задача Вот
- 11. Расстояние от
- 12. Дано: ВК- биссектриса, СМ||ВК Доказательство: Так как
- 13. Свойства медиан Теорема: Если a, b, с-
- 14.
- 16. Задача
Слайд 2 Цель работы: обобщить и систематизировать знания по теме «Треугольники».
Рассмотреть виды треугольников.
Доказать основные признаки и свойства треугольников.
Показать использование знаний по теме при решении задач.
Слайд 3Треугольник
простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны;
часть плоскости,
замкнутая ломаная линия с тремя звеньями.
Слайд 4Элементы треугольника
Медиана
Высота
Биссектриса
Средняя линия
BM= MC
AD=DC
AK=KB
BM= MA
AN=NC
MN // BC
BC=2·MN
BH AC
AH1
CH2 AB
P
D
K
H2
H1
N
P
∠ABM= ∠MBC ∠BCP= ∠PCA
∠CAN= ∠NAB
Слайд 5Виды треугольников по сторонам
Равносторонний
Равнобедренный
Разносторонний
Углы при основании равны;
Медиана является биссектрисой и высотой.
Все
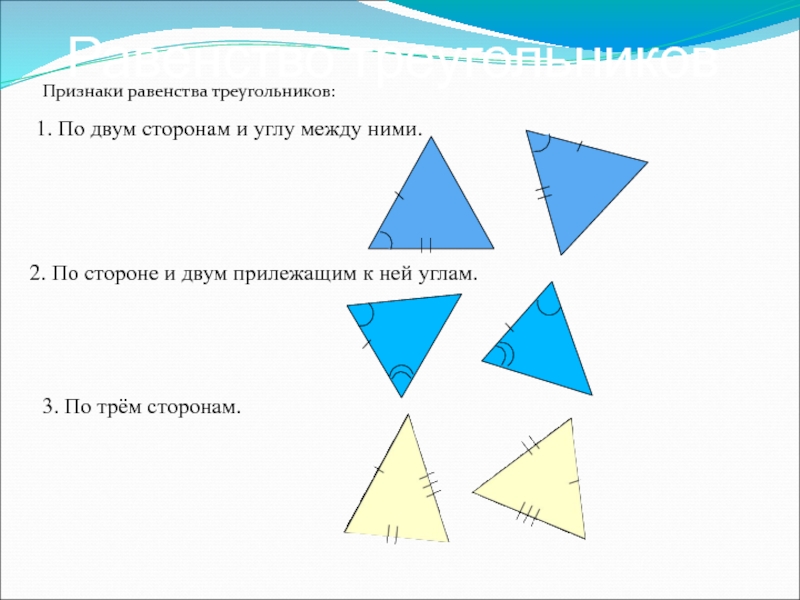
Слайд 7Равенство треугольников
Признаки равенства треугольников:
2. По стороне и двум прилежащим к ней
3. По трём сторонам.
1. По двум сторонам и углу между ними.
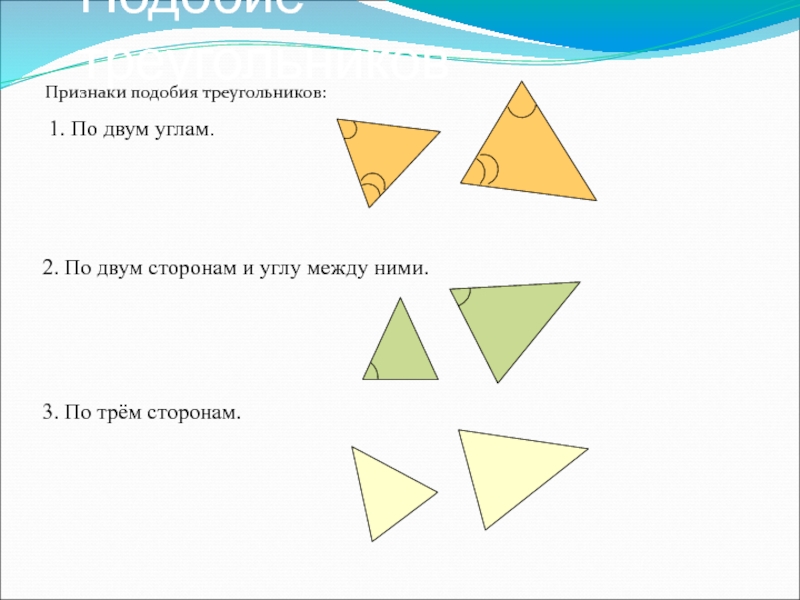
Слайд 8Подобие треугольников
Признаки подобия треугольников:
1. По двум углам.
2. По двум сторонам и
3. По трём сторонам.
Слайд 10 Задача
Вот задача индийского математика 12в. Бхаскары
На
Решение:
По теореме Пифагора находим СD:
CD = 3 + 4 = 9 + 16 =25 => CD= 5.
Высота тополя равна: CB+CA. Т.к. CD=CB =>
AB=AC+CD= 3 + 5 = 8.
Ответ: высота тополя 8 футов.
2
2
2
Слайд 11 Расстояние от инцентра треугольника до его
Теорема 1: Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные соответствующим боковым сторонам.
Следствие: Пусть AL-биссектриса ∠А в ΔАВС. Тогда отрезки CL и LB находятся по формулам: , .