- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Третя ознака рівності трикутників презентация
Содержание
- 1. Третя ознака рівності трикутників
- 2. Означення Трикутник – замкнена ламана з трьох
- 3. Медіана трикутника – відрізок, що сполучає
- 4. Бісектриса трикутника це відрізок бісектриси кута трикутника
- 5. Висота трикутника це перпендикуляр, опущений з вершини
- 6. Сума кутів трикутника Сума кутів трикутника дорівнює
- 7. Зовнішній кут трикутника кут, утворений стороною трикутника
- 8. Рівність геометричних фігур Якщо фігури можна сумістити
- 9. Перша ознака рівності трикутників Якщо дві сторони
- 10. Друга ознака рівності трикутників Якщо сторона і
- 11. Рівнобедрений трикутник ΔАВС – рівнобедрений; АВ
- 12. Властивість рівнобедреного трикутника Теорема 12. У рівнобедреного
- 13. Ознака рівнобедреного трикутника Теорема 13. Якщо в
- 14. Третя ознака рівності трикутників Теорема 14. Якщо
- 15. Запропонуй доведення, коли … Вершина А належить
- 16. Побудова трикутника за трьома сторонами
- 17. Висновки Трикутник однозначно визначається: двома сторонами і
- 18. Застосуй отримані знання У трикутниках АВС і
- 19. Застосуй отримані знання Чи правильно, що два
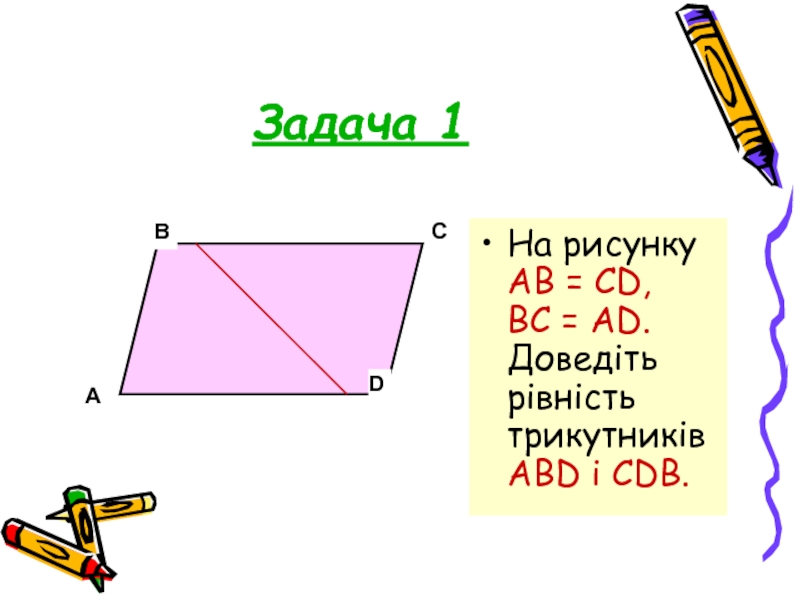
- 20. Задача 1 На рисунку АВ = CD,
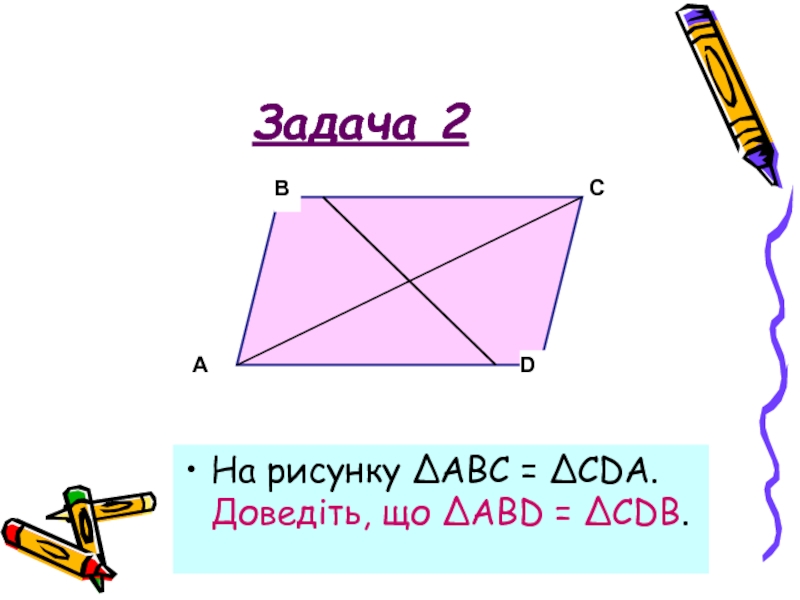
- 21. Задача 2 На рисунку ΔАВС = ΔCDA. Доведіть, що ΔABD = ΔCDB.
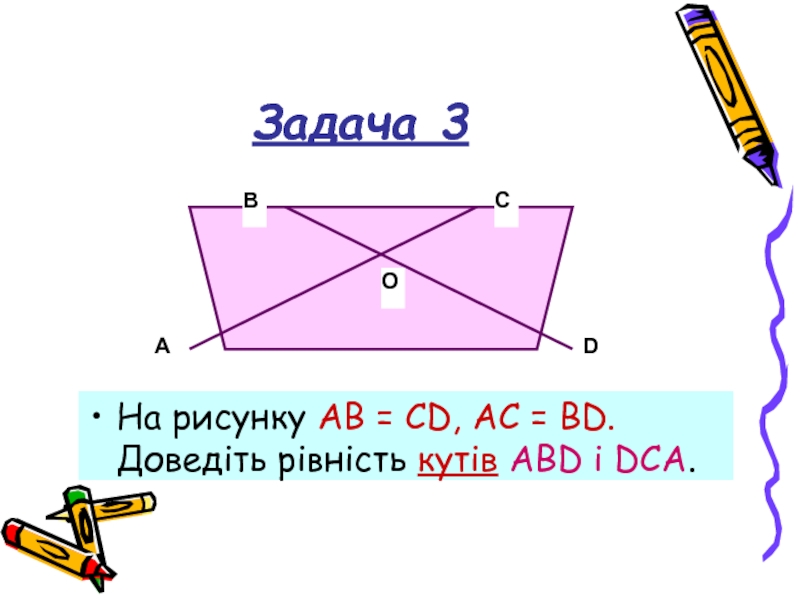
- 22. Задача 3 На рисунку АВ = CD,
- 23. Обґрунтуйте Δ АВС = Δ MNK; Δ
- 24. Висновки
Означення Трикутник – замкнена ламана з трьох ланок. Запис: ΔАВС Точки А, В, С – вершини Відрізки АВ, ВС, СА – сторони Р = АВ + ВС + СА. ∠А, ∠В,
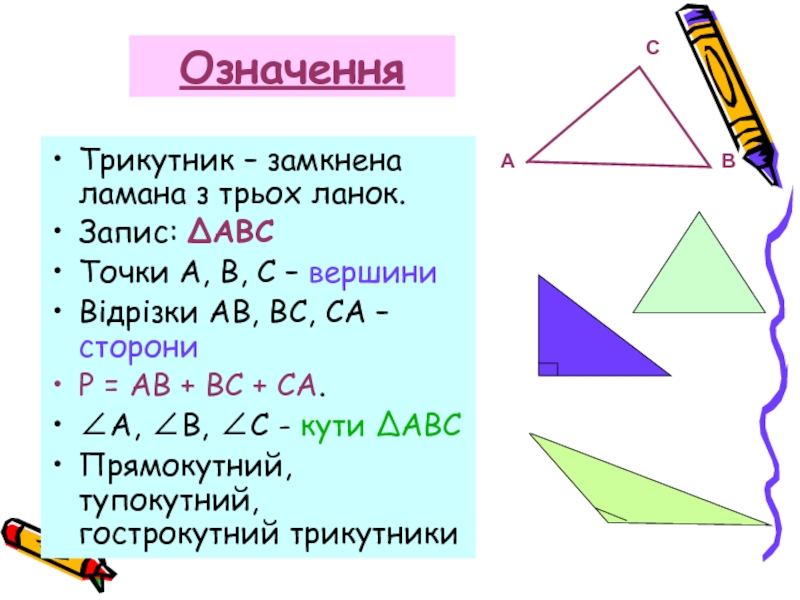
Слайд 2Означення
Трикутник – замкнена ламана з трьох ланок.
Запис: ΔАВС
Точки А, В, С
– вершини
Відрізки АВ, ВС, СА – сторони
Р = АВ + ВС + СА.
∠А, ∠В, ∠С - кути ΔАВС
Прямокутний, тупокутний, гострокутний трикутники
Відрізки АВ, ВС, СА – сторони
Р = АВ + ВС + СА.
∠А, ∠В, ∠С - кути ΔАВС
Прямокутний, тупокутний, гострокутний трикутники
С
В
А
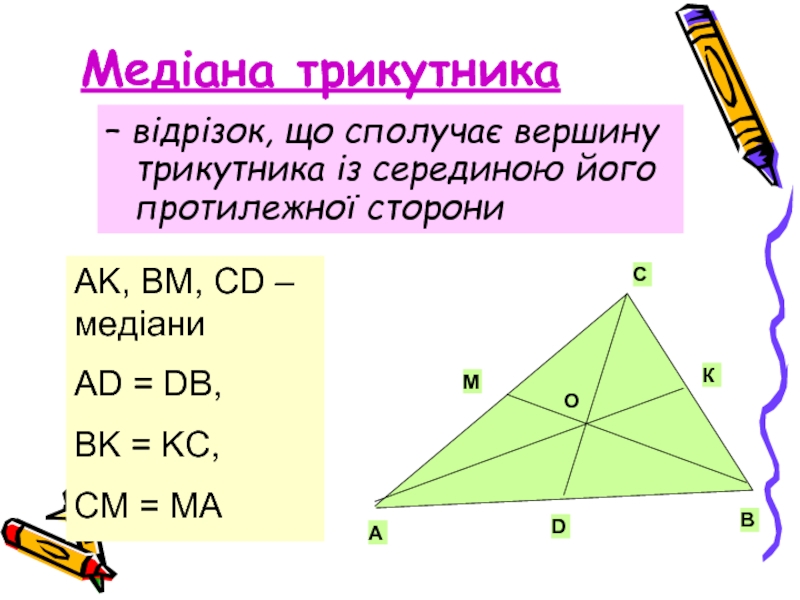
Слайд 3Медіана трикутника
– відрізок, що сполучає вершину трикутника із серединою його
протилежної сторони
AK, BM, CD –медіани
AD = DB,
BK = KC,
CM = MA
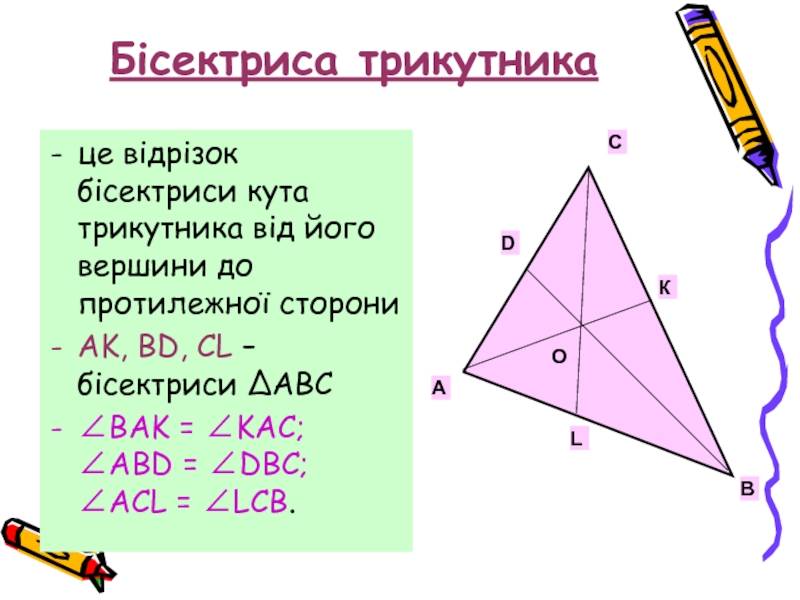
Слайд 4Бісектриса трикутника
це відрізок бісектриси кута трикутника від його вершини до протилежної
сторони
AK, BD, CL –бісектриси ΔABC
∠BAK = ∠KAC; ∠ABD = ∠DBC; ∠ACL = ∠LCB.
AK, BD, CL –бісектриси ΔABC
∠BAK = ∠KAC; ∠ABD = ∠DBC; ∠ACL = ∠LCB.
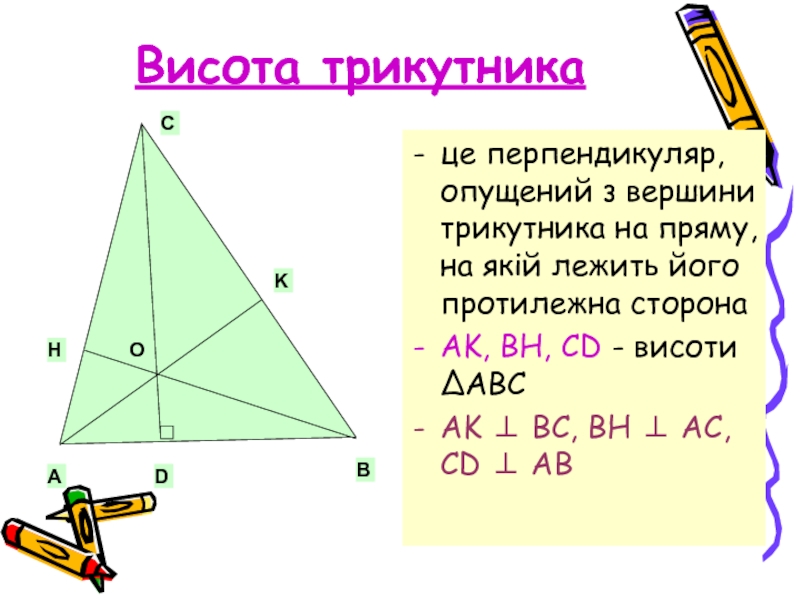
Слайд 5Висота трикутника
це перпендикуляр, опущений з вершини трикутника на пряму, на якій
лежить його протилежна сторона
AK, BH, CD - висоти ΔABC
AK ⊥ BC, BH ⊥ AC, CD ⊥ AB
AK, BH, CD - висоти ΔABC
AK ⊥ BC, BH ⊥ AC, CD ⊥ AB
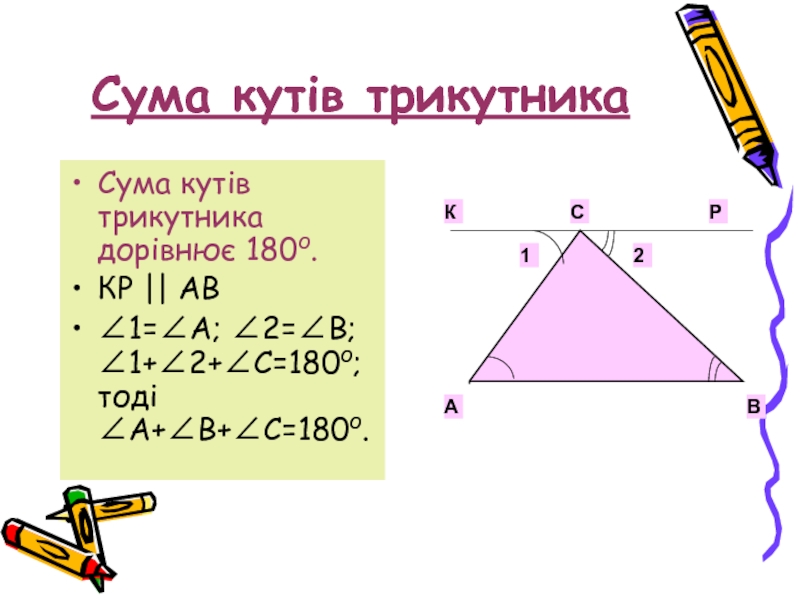
Слайд 6Сума кутів трикутника
Сума кутів трикутника дорівнює 180о.
КР || АВ
∠1=∠А; ∠2=∠В; ∠1+∠2+∠С=180о;
тоді
∠А+∠В+∠С=180о.
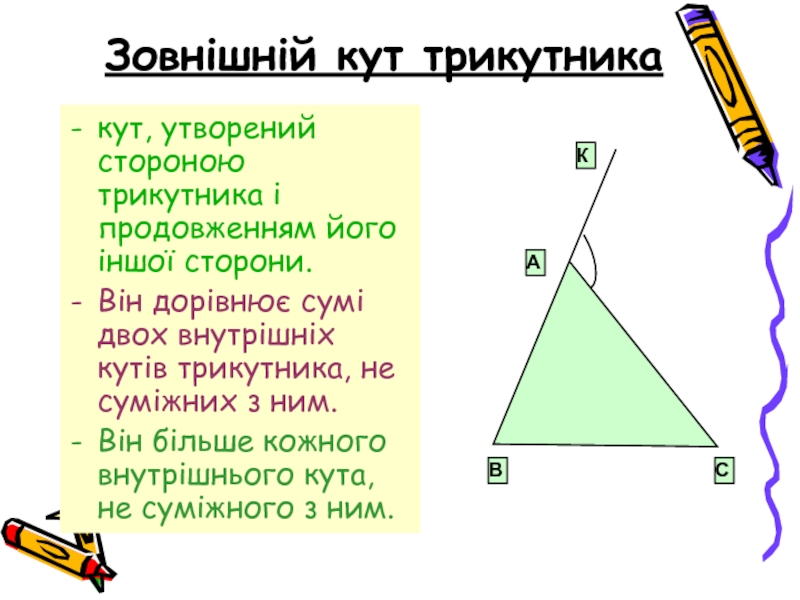
Слайд 7Зовнішній кут трикутника
кут, утворений стороною трикутника і продовженням його іншої сторони.
Він
дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним.
Він більше кожного внутрішнього кута, не суміжного з ним.
Він більше кожного внутрішнього кута, не суміжного з ним.
Слайд 8Рівність геометричних фігур
Якщо фігури можна сумістити рухом, то вони рівні
Якщо кожна
з двох фігур дорівнює третій, то перша і друга фігури рівні.
ΔABC = ΔКРТ, тоді розуміють, що ∠А = ∠К, ∠В = ∠Р, ∠С = ∠Т, АВ = КР, АС = КТ, ВС = РТ.
ΔABC = ΔКРТ, тоді розуміють, що ∠А = ∠К, ∠В = ∠Р, ∠С = ∠Т, АВ = КР, АС = КТ, ВС = РТ.
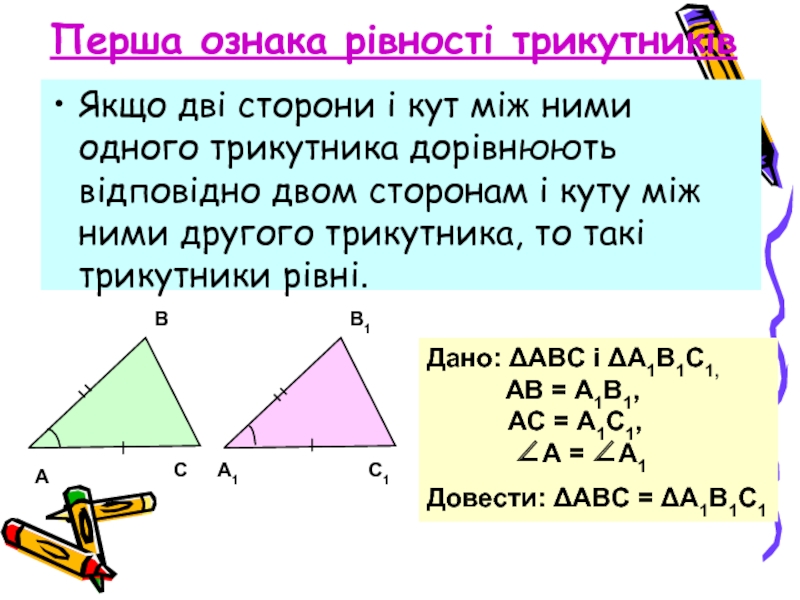
Слайд 9Перша ознака рівності трикутників
Якщо дві сторони і кут між ними одного
трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.
Дано: ΔАВС і ΔА1В1С1,
АВ = А1В1,
АС = А1С1,
∠А = ∠А1
Довести: ΔАВС = ΔА1В1С1
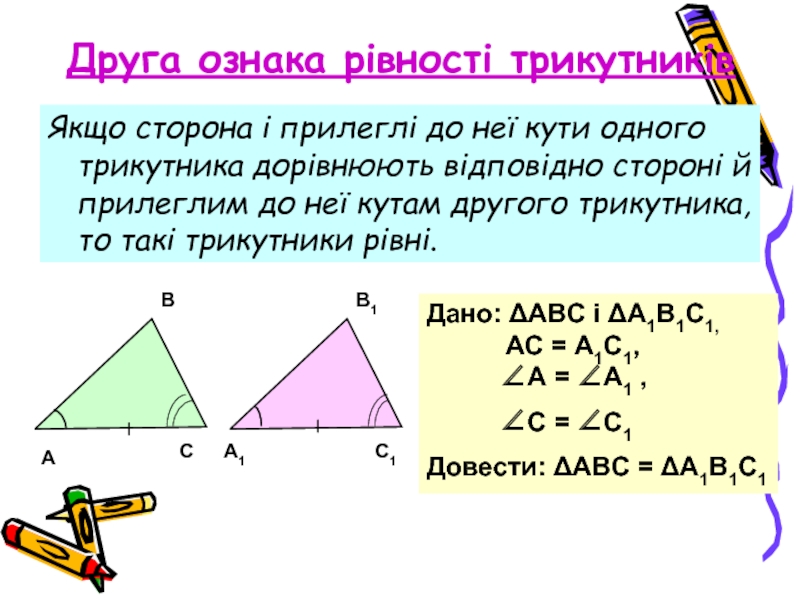
Слайд 10Друга ознака рівності трикутників
Якщо сторона і прилеглі до неї кути одного
трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
Дано: ΔАВС і ΔА1В1С1,
АС = А1С1,
∠А = ∠А1 ,
∠C = ∠C1
Довести: ΔАВС = ΔА1В1С1
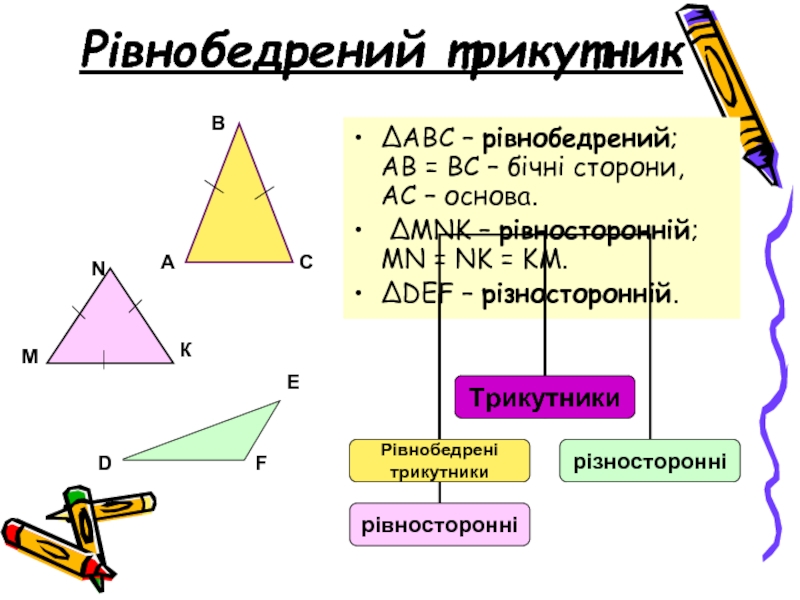
Слайд 11Рівнобедрений трикутник
ΔАВС – рівнобедрений;
АВ = ВС – бічні сторони,
АС
– основа.
ΔMNK – рівносторонній; MN = NK = KM.
ΔDEF – різносторонній.
ΔMNK – рівносторонній; MN = NK = KM.
ΔDEF – різносторонній.
Слайд 12Властивість рівнобедреного трикутника
Теорема 12. У рівнобедреного трикутника кути при основі рівні,
а бісектриса, проведена до основи, є медіаною і висотою.
ΔАВС – рівнобедрений, ВС – основа.
АL –бісектриса, тому ∠ВАL=∠CAL; ΔBAL=ΔCAL (AB=AC, AL – спільна сторона, ∠ВАL=∠LAC);
Отже, ∠В=∠С, тобто кути при основі ΔАВС рівні;
BL=CL, тобто AL – медіана ΔАВС;
∠ALB=∠ALC=90o, тобто AL – висота ΔАВС.
Слайд 13Ознака рівнобедреного трикутника
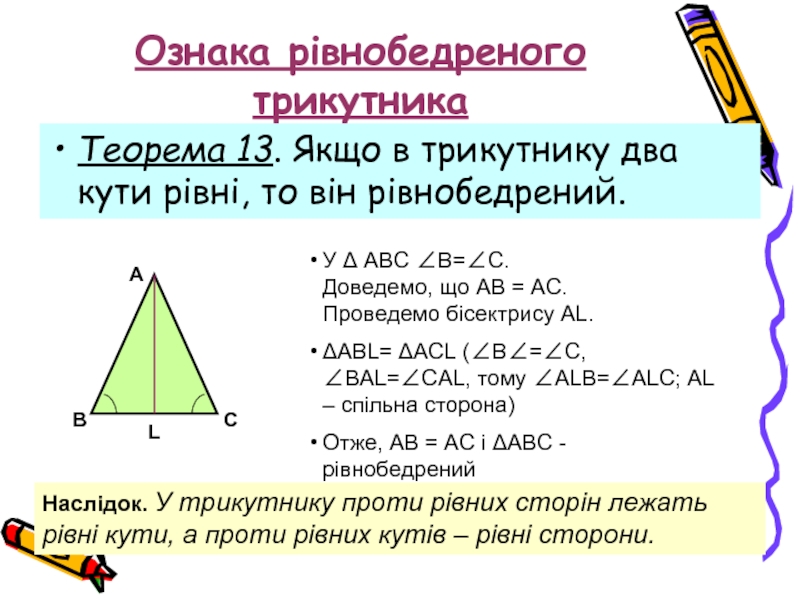
Теорема 13. Якщо в трикутнику два кути рівні, то
він рівнобедрений.
У Δ АВС ∠В=∠С.
Доведемо, що АВ = АС.
Проведемо бісектрису AL.
ΔАВL= ΔACL (∠B∠=∠C, ∠BAL=∠CAL, тому ∠ALB=∠ALC; AL – спільна сторона)
Отже, АВ = АС і ΔАВС - рівнобедрений
Наслідок. У трикутнику проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.
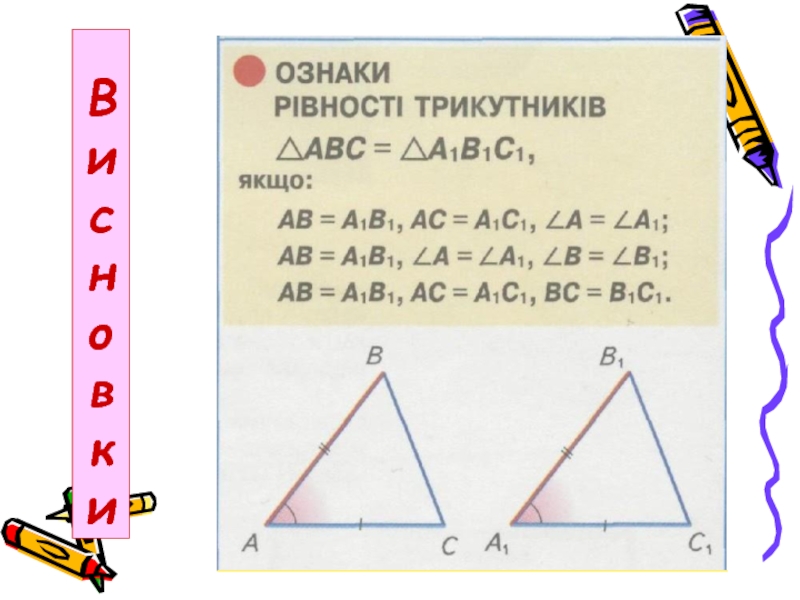
Слайд 14Третя ознака рівності трикутників
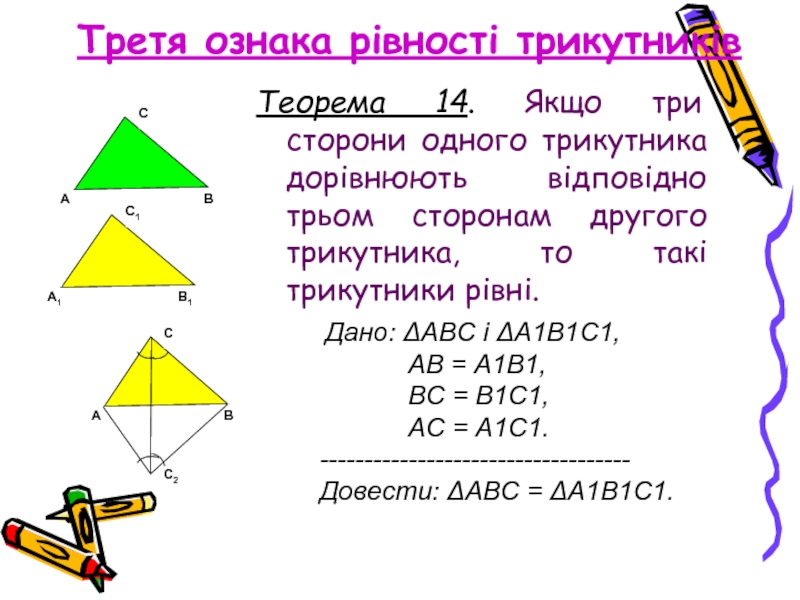
Теорема 14. Якщо три сторони одного трикутника дорівнюють
відповідно трьом сторонам другого трикутника, то такі трикутники рівні.
Дано: ΔАВС і ΔА1В1С1,
АВ = А1В1,
ВС = В1С1,
АС = А1С1.
----------------------------------- Довести: ΔАВС = ΔА1В1С1.
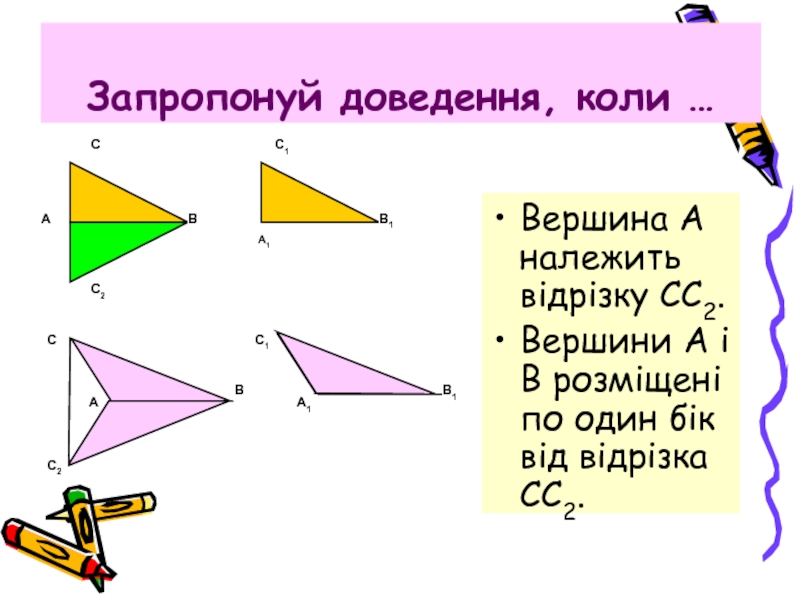
Слайд 15Запропонуй доведення, коли …
Вершина А належить відрізку СС2.
Вершини А і
В розміщені по один бік від відрізка СС2.
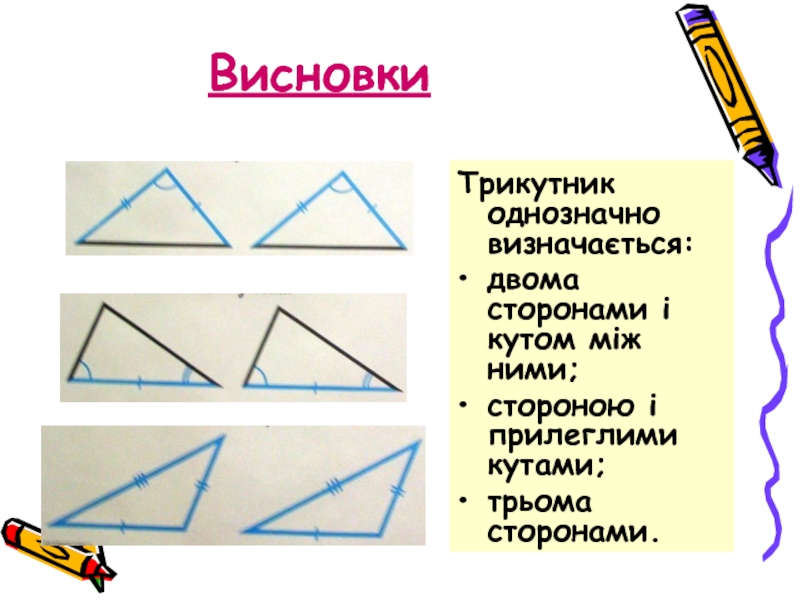
Слайд 17Висновки
Трикутник однозначно визначається:
двома сторонами і кутом між ними;
стороною і прилеглими кутами;
трьома
сторонами.
Слайд 18Застосуй отримані знання
У трикутниках АВС і А1В1С1 АС = А1С1,
ВС
= В1С1. Яку рівність необхідно додати до умови, щоб рівність даних трикутників можна було довести за третьою ознакою?
Три сторони одного трикутника дорівнюють трьом сторонам другого трикутника. Чи є рівними кути між відповідно рівними сторонами цих трикутників? Чому?
Три сторони одного трикутника дорівнюють трьом сторонам другого трикутника. Чи є рівними кути між відповідно рівними сторонами цих трикутників? Чому?
Слайд 19Застосуй отримані знання
Чи правильно, що два рівносторонні трикутники рівні, якщо вони
мають однакові периметри?
Чи правильно, що два довільні трикутники рівні, якщо вони мають однакові периметри?
Чи виконується обернене твердження?
Чи правильно, що два довільні трикутники рівні, якщо вони мають однакові периметри?
Чи виконується обернене твердження?
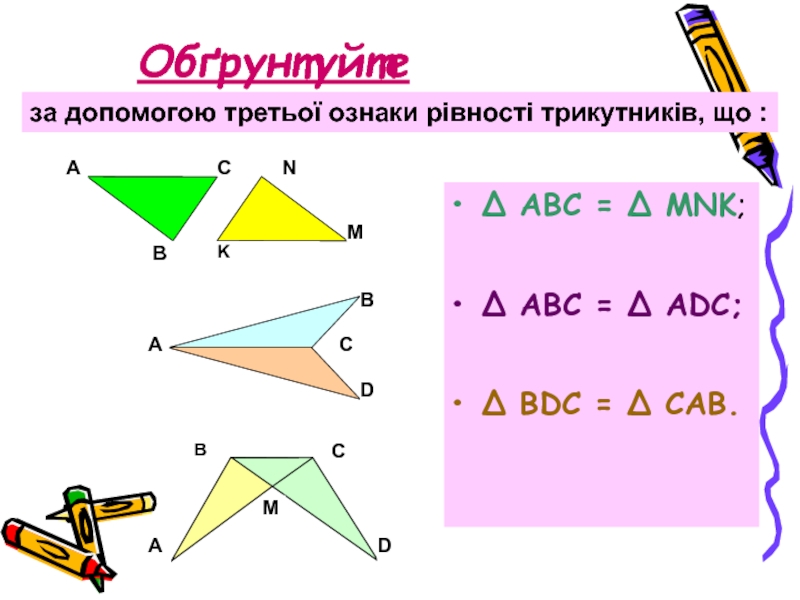
Слайд 23Обґрунтуйте
Δ АВС = Δ MNK;
Δ АВС = Δ ADC;
Δ BDC =
Δ CAB.
за допомогою третьої ознаки рівності трикутників, що :
