- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Транспортные задачи презентация
Содержание
- 1. Транспортные задачи
- 2. Постановка задачи Транспортная задача - одна из
- 3. Первый точный метод решения ТЗ разработан Л.
- 4. Матрица системы ограничений ТЗ настолько своеобразна, что
- 5. Общим для ТЗ является распределение ресурсов, находящихся
- 6. Задачи, относящиеся к транспортным: прикрепление потребителей
- 7. 2. Экономико-математическая модель транспортной задачи Дано: Множество
- 8. Математическая запись /18
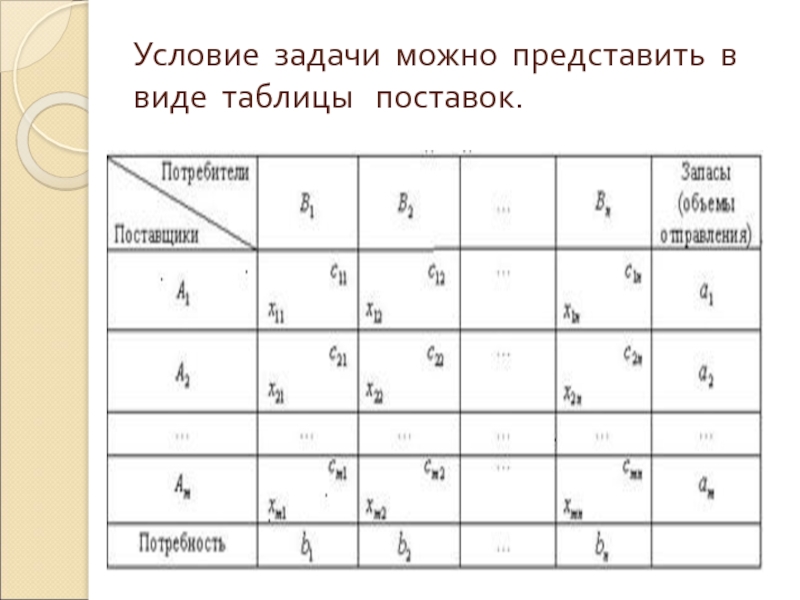
- 9. Условие задачи можно представить в виде таблицы поставок.
- 10. Транспортная задача называется закрытой, если суммарный объем
- 11. Открытую задачу необходимо привести к закрытой форме.
- 12. Варианты, связывающие фиктивные пункты с реальными,
- 13. Особенности ТЗ: распределению подлежат однородные ресурсы; условия
- 14. Транспортные задачи могут решаться симплекс-методом.
- 15. 3. Пример 4 предприятия для производства продукции
- 16. Тарифы перевозок известны и задаются матрицей
- 17. Требуется составить план перевозок, при котором общая
Слайд 1Транспортные задачи
План:
Постановка задачи
Экономико-математическая модель задачи
Пример составления ЭММ транспортной задачи.
Слайд 2Постановка задачи
Транспортная задача - одна из наиболее распространенных специальных задач линейного
программирования.
Первая строгая постановка транспортной задачи принадлежит Ф.Хичкоку (1941 г.) , поэтому в зарубежной литературе ее называют проблемой Хичкока.
Первая строгая постановка транспортной задачи принадлежит Ф.Хичкоку (1941 г.) , поэтому в зарубежной литературе ее называют проблемой Хичкока.
Слайд 3Первый точный метод решения ТЗ разработан Л. В. Канторовичем и М.
К. Гавуриным в1949 г.
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью.
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью.
Слайд 4Матрица системы ограничений ТЗ настолько своеобразна, что для ее решения разработаны
специальные методы.
Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Слайд 5Общим для ТЗ является распределение ресурсов, находящихся у m производителей
(поставщиков), по n потребителям этих ресурсов.
Критерии оптимальности:
Критерий стоимости (минимум затрат на реализацию плана перевозок);
Критерий времени (минимум времени) и др.
Критерии оптимальности:
Критерий стоимости (минимум затрат на реализацию плана перевозок);
Критерий времени (минимум времени) и др.
Слайд 6Задачи, относящиеся к транспортным:
прикрепление потребителей ресурса к производителям;
привязка пунктов отправления к
пунктам назначения;
взаимная привязка грузопотоков прямого и обратного направлений;
отдельные задачи оптимальной загрузки промышленного оборудования;
оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.
взаимная привязка грузопотоков прямого и обратного направлений;
отдельные задачи оптимальной загрузки промышленного оборудования;
оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.
Слайд 72. Экономико-математическая модель транспортной задачи
Дано:
Множество I, включающее m пунктов отправления груза,
имеющегося в количествах ai (i=1…m)
Множество J, включающее n пунктов потребления, в каждом из которых имеется спрос на данный груз в количестве bj (j=1…n)
Затраты cij на перевозку единицы груза между пунктами i и j
Найти:
План перевозок X = (xij), согласно которому груз из пунктов отправления перевозится в пункты потребления с минимальными транспортными издержками, а спрос удовлетворяется полностью.
Множество J, включающее n пунктов потребления, в каждом из которых имеется спрос на данный груз в количестве bj (j=1…n)
Затраты cij на перевозку единицы груза между пунктами i и j
Найти:
План перевозок X = (xij), согласно которому груз из пунктов отправления перевозится в пункты потребления с минимальными транспортными издержками, а спрос удовлетворяется полностью.
/18
Слайд 10Транспортная задача называется закрытой, если суммарный объем отправляемых грузов .равен суммарному
объему потребности в этих грузах по пунктам назначения, т.е.
В противном случае, ТЗ называется открытой.
В противном случае, ТЗ называется открытой.
Слайд 11Открытую задачу необходимо привести к закрытой форме.
В случае, если:
потребности
по пунктам потребления превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;
запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.
запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.
Слайд 12
Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки.
После введения
фиктивных пунктов задача решается как закрытая.
Слайд 13Особенности ТЗ:
распределению подлежат однородные ресурсы;
условия задачи описываются только уравнениями;
все переменные выражаются
в одинаковых единицах измерения;
во всех уравнениях коэффициенты при неизвестных равны единице;
каждая неизвестная встречается только в двух уравнениях системы ограничений.
во всех уравнениях коэффициенты при неизвестных равны единице;
каждая неизвестная встречается только в двух уравнениях системы ограничений.
Слайд 14
Транспортные задачи могут решаться симплекс-методом.
Однако перечисленные особенности позволяют для транспортных
задач применять более простые методы решения.
Слайд 153. Пример
4 предприятия для производства продукции используют некоторое сырьё. Спрос на
сырьё каждого из предприятий соответственно составляет: 120, 50, 190 и 110 у.ед.
Сырьё сосредоточено в трёх местах. Предложения поставщиков сырья равны: 160, 140 и 170 у.ед.
На каждое предприятие сырьё может завозиться от любого поставщика.
5
Сырьё сосредоточено в трёх местах. Предложения поставщиков сырья равны: 160, 140 и 170 у.ед.
На каждое предприятие сырьё может завозиться от любого поставщика.
5
Слайд 16
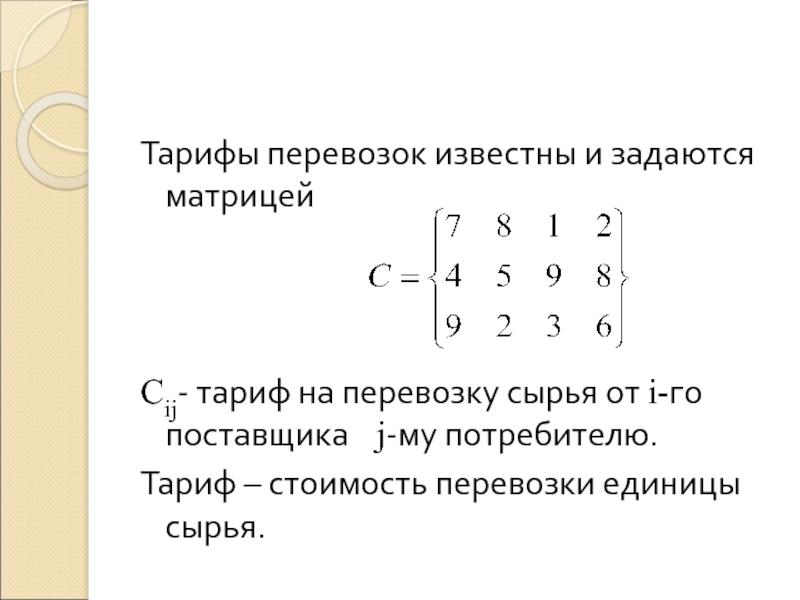
Тарифы перевозок известны и задаются матрицей
Сij- тариф на перевозку сырья от
i-го поставщика j-му потребителю.
Тариф – стоимость перевозки единицы сырья.
Тариф – стоимость перевозки единицы сырья.
Слайд 17Требуется составить план перевозок, при котором общая стоимость перевозок минимальна.
Построение ЭММ
задачи
Пусть хij- количество сырья, перевозимого от i-го поставщика
j-му потребителю.
Пусть хij- количество сырья, перевозимого от i-го поставщика
j-му потребителю.