- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Транспортная задача презентация
Содержание
- 1. Транспортная задача
- 2. Формулировка транспортной задачи Транспортная задача в
- 3. Неизвестными
- 4. Рассмотрим задачу с первым критерием (минимальная
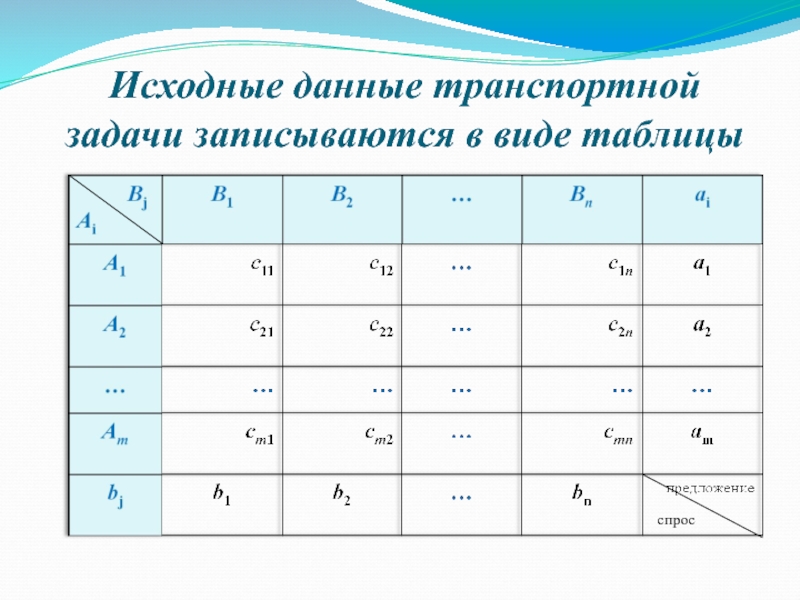
- 5. Исходные данные транспортной задачи записываются в виде таблицы спрос
- 6. Целевая функция имеет вид:
- 7. Система ограничений состоит из двух групп уравнений
- 8. Вторая группа из n уравнений
- 9. Формулировка транспортной задачи такова: Найти переменные задачи
- 10. Пример: Данные задачи представлены
- 11. Решение: Пусть xij - объемы перевозок груза
- 12. при ограничениях 1) (Условие
- 13. Опорный и оптимальный план транспортной задачи
- 14. Необходимое и достаточное условие разрешимости транспортной задачи
- 15. Искусственные потребители и поставщики Если спрос меньше
- 16. Используемая литература: Борзунова Т.Л., Барыкин М.П. ,
Слайд 1Презентация к курсу:
«Исследование операций»
Тема:
«Транспортная задача»
Выполнила:
студентка 5 курса,
факультета Математики, Информатики,
Группы И - 51
Ченцова Е.А.
Научный руководитель:
Астахова Н.А. к. п. н. , доцент
Слайд 2Формулировка
транспортной задачи
Транспортная задача в общем виде состоит в определении оптимального
В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки.
Слайд 3
Неизвестными транспортной задачи являются объёмы перевозок
В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, фабрики, склады, магазины и т.д. Под стоимостью перевозок понимают тарифы, расстояния, время, расход топлива и т.п.
Слайд 4 Рассмотрим задачу с первым критерием (минимальная стоимость перевозок всего груза),
Слайд 7Система ограничений состоит из двух групп уравнений
Первая группа из
i = 1, 2, …, m.
Слайд 8 Вторая группа из n уравнений выражает требование полностью удовлетворить
j = 1, 2,…, n
Кроме этого, переменные задачи должны быть неотрицательны:
i = 1, 2, …, m
j = 1, 2, …, n
Слайд 9Формулировка транспортной задачи такова:
Найти переменные задачи
удовлетворяющие системе ограничений ,
i =
j = 1, 2, …, n
а также условию неотрицательности переменных
и обеспечивающие минимум целевой функции
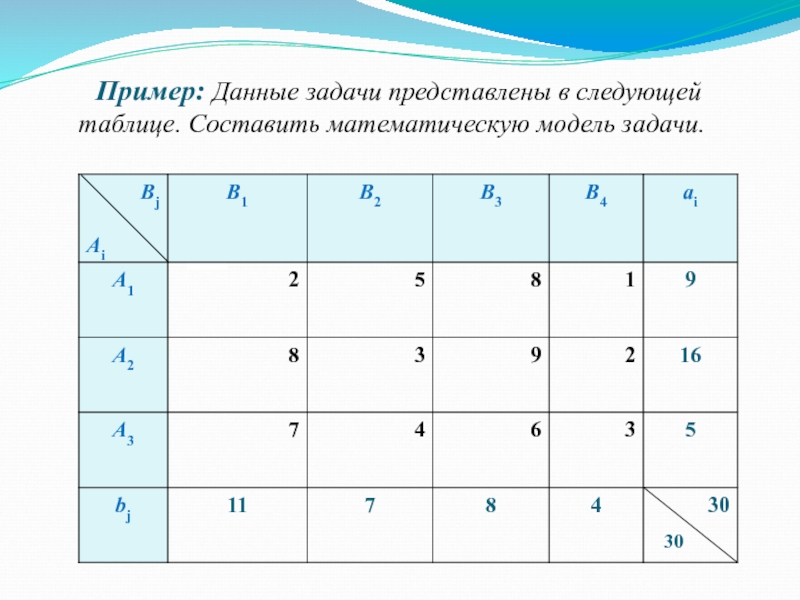
Слайд 10 Пример: Данные задачи представлены в следующей таблице. Составить
30
Слайд 11Решение: Пусть xij - объемы перевозок груза от i-го поставщика –
Целевая функция имеет вид :
Слайд 13Опорный и оптимальный план транспортной задачи
Всякое неотрицательное решение систем ограничений
Слайд 14Необходимое и достаточное условие разрешимости транспортной задачи
Если общее количество груза
Модель такой задачи называется закрытой,
в противном случае открытой.
Слайд 15Искусственные потребители и поставщики
Если спрос меньше предложения, то необходимо вводить искусственного
Если спрос больше предложения, то необходимо вводить искусственного поставщика Am+1
Слайд 16Используемая литература:
Борзунова Т.Л., Барыкин М.П. , Данилов Е.А. Соловьева О.Ю. -
Конюховский П.В. Математические методы исследования операций в экономике – СПб: Питер, 2000.