- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
The binomial model for option pricing презентация
Содержание
- 1. The binomial model for option pricing
- 2. Gurzuf, Crimea, June 2001 Contents European
- 3. Gurzuf, Crimea, June 2001 European Call Option
- 4. Gurzuf, Crimea, June 2001 Geometric Brownian Motion S(y), 0≤y
- 5. Gurzuf, Crimea, June 2001 Black-Scholes Formula The
- 6. Gurzuf, Crimea, June 2001 The Multi Period
- 7. Gurzuf, Crimea, June 2001 The Multi Period
- 8. Gurzuf, Crimea, June 2001 The Multi Period
- 9. Gurzuf, Crimea, June 2001 The Multi Period Binomial Model
- 10. Gurzuf, Crimea, June 2001 The Multi Period
- 11. Gurzuf, Crimea, June 2001 The Multi Period
- 12. Gurzuf, Crimea, June 2001 The Multi Period
- 13. Gurzuf, Crimea, June 2001 Geometric Brownian Motion
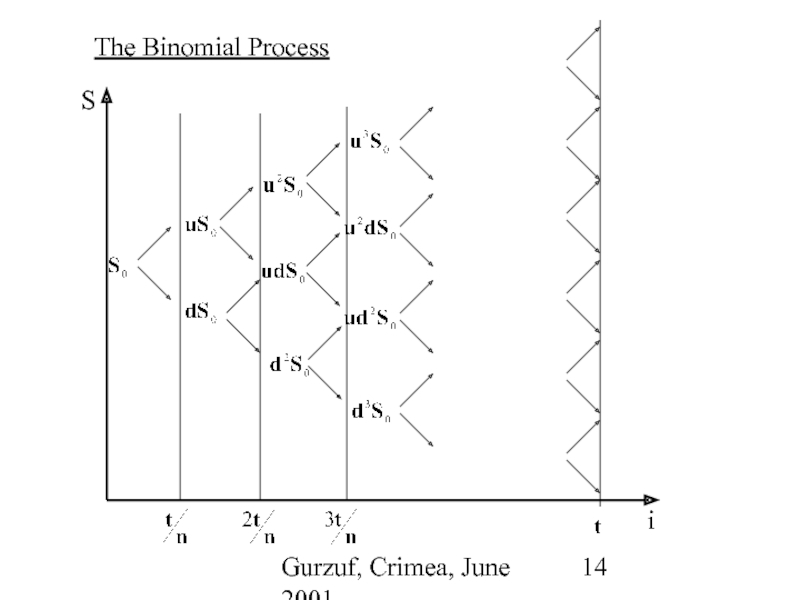
- 14. Gurzuf, Crimea, June 2001 The Binomial Process
- 15. Gurzuf, Crimea, June 2001 GBM as a
- 16. Gurzuf, Crimea, June 2001 GBM as a
- 17. Gurzuf, Crimea, June 2001 GBM as a
- 18. Gurzuf, Crimea, June 2001 GBM as a
- 19. Gurzuf, Crimea, June 2001 GBM as a limit By Central Limit Theorem
- 20. Gurzuf, Crimea, June 2001 GBM as a
- 21. Gurzuf, Crimea, June 2001 B-S Formula as
- 22. Gurzuf, Crimea, June 2001 B-S formula as
- 23. Gurzuf, Crimea, June 2001 B-S formula as
- 24. Gurzuf, Crimea, June 2001 B-S formula as a limit
- 25. Gurzuf, Crimea, June 2001 B-S formula as a limit Φ(·) is the N(0,1) distribution function
- 26. Gurzuf, Crimea, June 2001 B-S formula as a limit
- 27. Gurzuf, Crimea, June 2001 B-S formula as a limit where
Gurzuf, Crimea, June 2001 Contents European Call Option Geometric Brownian Motion Black-Scholes Formula Multi period Binomial Model GBM as a limit Black-Scholes Formula as a limit
Слайд 1Gurzuf, Crimea, June 2001
Option Pricing:
The Multi Period Binomial Model
Henrik Jönsson
Mälardalen University
Sweden
Слайд 2Gurzuf, Crimea, June 2001
Contents
European Call Option
Geometric Brownian Motion
Black-Scholes Formula
Multi period
Binomial Model
GBM as a limit
Black-Scholes Formula as a limit
GBM as a limit
Black-Scholes Formula as a limit
Слайд 3Gurzuf, Crimea, June 2001
European Call Option
C - Option Price
K - Strike
price
T - Expiration day
Exercise only at T
Payoff function, e.g.
T - Expiration day
Exercise only at T
Payoff function, e.g.
Слайд 4Gurzuf, Crimea, June 2001
Geometric Brownian Motion
S(y), 0≤y
geometric Brownian motion if
independent of all prices up to time y
independent of all prices up to time y
Слайд 5Gurzuf, Crimea, June 2001
Black-Scholes Formula
The price at time zero of a
European call
option (non-dividend-paying stock):
where
option (non-dividend-paying stock):
where
Слайд 6Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
i
S
i=1,2,…
Note:
u and
d the same for all moments i
d < 1+r < u, where r is the risk-free interest rate
d < 1+r < u, where r is the risk-free interest rate
Слайд 7Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
Let
Let (X1, X2,…,
Xn) be the vector describing the outcome after n steps.
Find the set of probabilities P{X1=x1, X2 =x2,…, Xn =xn}, xi=0,1, i=1,…,n, such that there is no arbitrage opportunity.
Find the set of probabilities P{X1=x1, X2 =x2,…, Xn =xn}, xi=0,1, i=1,…,n, such that there is no arbitrage opportunity.
i=1,2,…
Слайд 8Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
Choose an arbitrary vector
(α1, α2, …, αn-1)
If A={X1= α1, X2= α2, …, Xn-1= αn-1} is true buy one unit of stock and sell it back at moment n
Probability that the stock is purchased qn-1=P{X1= α1, X2= α2, …, Xn-1= αn-1}
Probability that the stock goes up pn= P{Xn=1| X1= α1, …, Xn-1= αn-1}
If A={X1= α1, X2= α2, …, Xn-1= αn-1} is true buy one unit of stock and sell it back at moment n
Probability that the stock is purchased qn-1=P{X1= α1, X2= α2, …, Xn-1= αn-1}
Probability that the stock goes up pn= P{Xn=1| X1= α1, …, Xn-1= αn-1}
Слайд 10Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
Expected gain =
No
arbitrage opportunity implies
qn-1[pn(1+r)-1uSn-1+(1- pn) (1+r)-1dSn-1-Sn-1]
r = risk-free interest rate
Слайд 11Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
(α1, α2, …, αn-1)
arbitrary vector
No arbitrage opportunity
⇓
No arbitrage opportunity
⇓
X1,…, Xn independent with P{Xi=1}=p, i=1,…,n
Risk-free interest rate r the same for all moments i
Слайд 12Gurzuf, Crimea, June 2001
The Multi Period Binomial Model
Limitations:
Two outcomes only
The
same increase & decrease for all time periods
The same probabilities
The same probabilities
Qualities:
Simple mathematics
Arbitrage pricing
Easy to implement
Слайд 18Gurzuf, Crimea, June 2001
GBM as a limit
Expected value of W
Variance of
W
EY = np
VarY = np(1-p)
Слайд 20Gurzuf, Crimea, June 2001
GBM as a limit
The multi period Binomial model
becomes geometric Brownian motion when n → ∞, since
are independent
are independent
Слайд 21Gurzuf, Crimea, June 2001
B-S Formula as a limit
Let
, Y ~ Bin(n,p)
The value of the option after n periods =
where S(t)= uY dn-Y S(0)
The value of the option after n periods =
where S(t)= uY dn-Y S(0)
max[S(t)-K,0] = [S(t)-K]+
No arbitrage ⇒
Слайд 22Gurzuf, Crimea, June 2001
B-S formula as a limit
The unique non-arbitrage option
price
As n → ∞
As n → ∞
X~N(0,1)
