- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей (ТВ) презентация
Содержание
- 1. Теория вероятностей (ТВ)
- 2. В современном мире автоматизации производства теория вероятности(Т.В)
- 3. Под случайным событием понимается всякое явление, о
- 4. Основные понятия и термины ТВ Наблюдения,
- 5. Основные понятия и термины ТВ Результат испытания
- 6. Основные понятия и термины ТВ Каждое событие обладает объективной возможностью наступления
- 8. Примеры: 1) При подбрасывании монеты появление цифры
- 9. Основные понятия и термины ТВ В
- 10. Основные понятия и термины ТВ Например,
- 11. Основные понятия и термины ТВ Событие
- 14. Виды событий в ТВ В зависимости
- 15. Виды случайных событий 1. Простое -
- 16. 2. Сложное (составное) событие - описывается несколькими
- 17. Виды сложных событий а) Логическая сумма (объединение)
- 18. Виды сложных событий Общепринятая запись суммы (объединения)
- 19. Сумма (объединение) трех событий:
- 20. б) Логическое произведение (пересечение) простых событий -
- 21. Виды сложных событий Например, событие
- 22. Общепринятая запись произведения (пересечения):
- 23. 3. Равновозможные события – имеют одинаковую объективную
- 24. События Виды случайных событий
- 25. События
- 26. 4. Единственно возможные события – такие, когда
- 27. Виды случайных событий 5. Независимые и зависимые
- 28. Виды случайных событий Система единственно возможных несовместных
- 29. Виды случайных событий 6. Противоположные события –
- 30. Виды случайных событий Так, противоположны события:
- 31. Конечное число несовместных равновозможных событий, образующих
- 32. Про опыт говорят, что он сводится
- 33. Например, в опыте выпадению герба
- 34. Численная мера объективной возможности появления
- 35. Классическое определение вероятности Оно не связано с
- 36. Классическое определение вероятности Тогда вероятность события может
- 37. Классическое определение вероятности Согласно формулы ( I
- 38. Классическое определение вероятности В формуле (I)
- 39. Классическое определение вероятности При
- 40. Классическое определение вероятности Обозначим
- 41. Классическое определение вероятности Недостаток: опыты редко сводятся
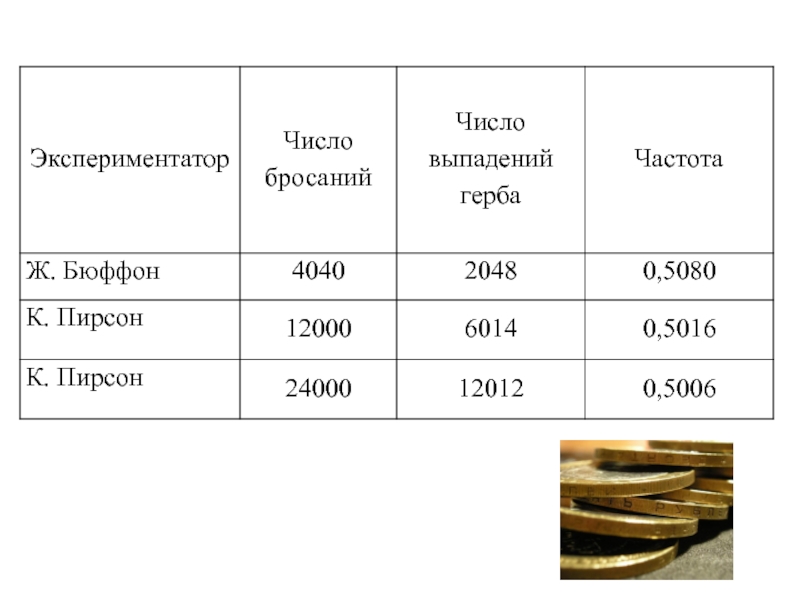
- 42. Статистическое определение вероятности Связано с проведением опытов
- 43. Статистическое определение вероятности Свойство устойчивости относительной частоты
- 44. На основании теоремы Бернулли : вероятность –
- 45. Практически статистическая вероятность может быть найдена
- 46. Недостаток - необходимость выполнения бесконечного числа опытов
- 47. Формулы ( I ) и ( II
- 48. Косвенные способы вычисления вероятностей Позволяют по известным
- 49. К ним относятся: - теоремы (аксиомы) ТВ;
- 50. Задачи по теме: «Вероятность. Понятие события и вероятности события»
- 51. 1. В урне 3 белых и 9
- 52. 2. Брошена игральная кость. Какова вероятность событий:
- 53. 3. Брошены 2 игральные кости. Какова вероятность
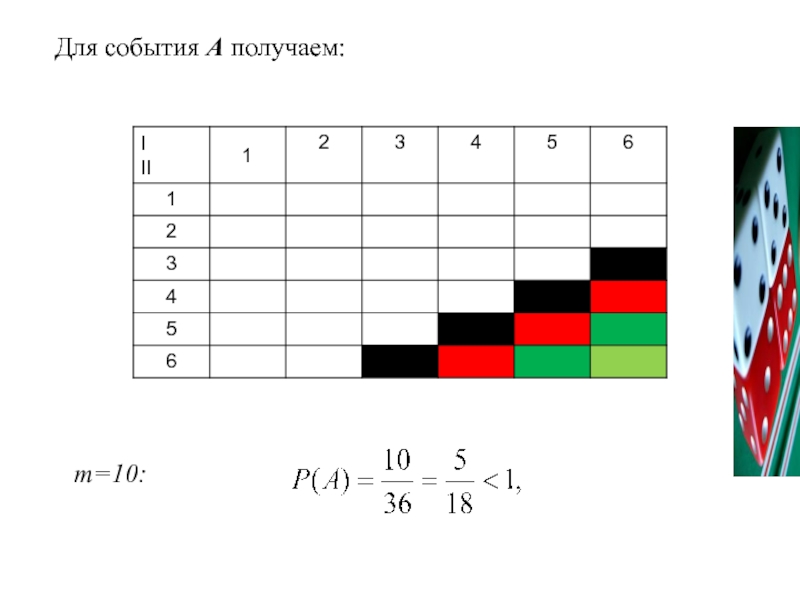
- 54. Для события А получаем: m=10:
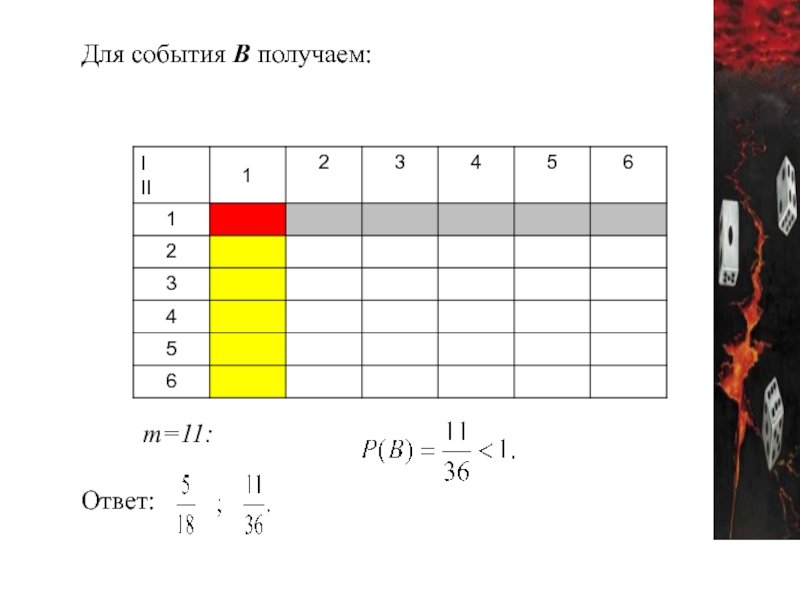
- 55. Для события В получаем: m=11: Ответ:
- 56. Основные теоремы ТВ Используются для вычисления вероятностей
- 57. Теорема сложения вероятностей Суммой событий называется
- 58. Теорема: Вероятность суммы двух или нескольких совместных
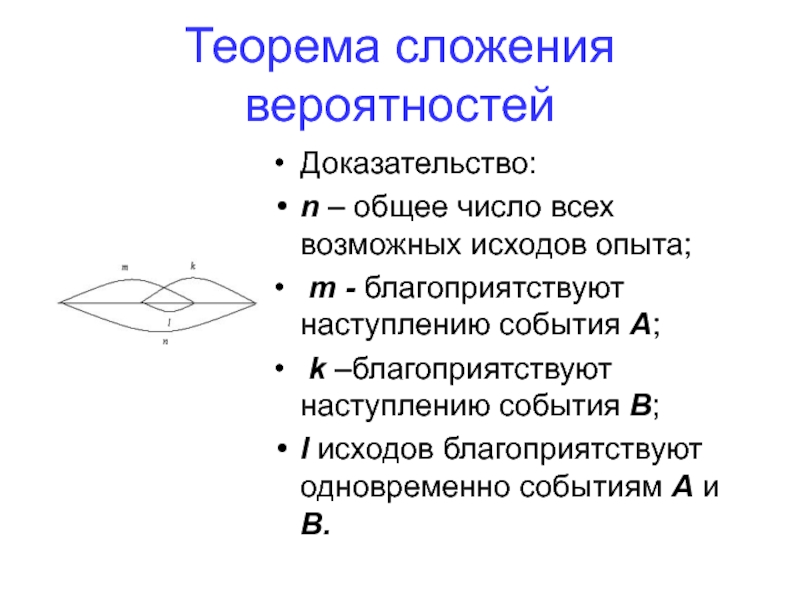
- 59. Теорема сложения вероятностей Доказательство: n – общее
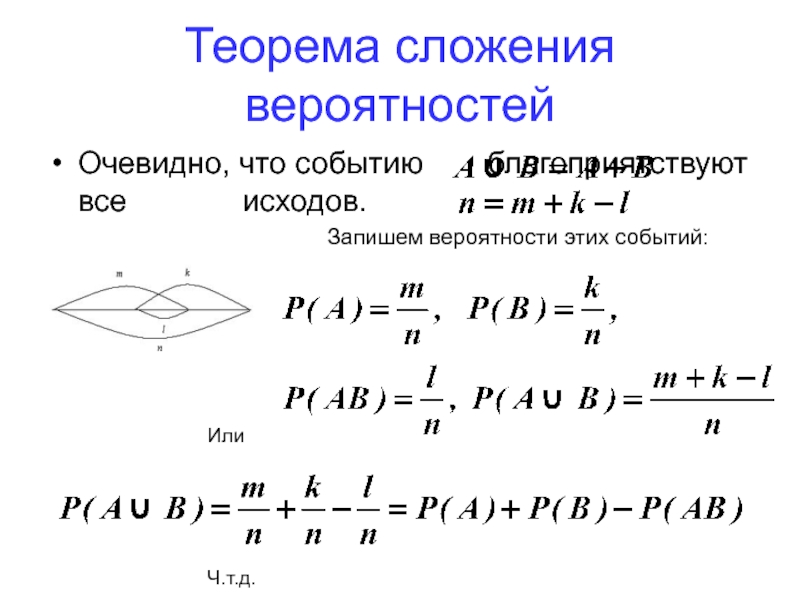
- 60. Очевидно, что событию благоприятствуют все
- 61. Теорема сложения вероятностей Для несовместных событий l
- 62. Задача 1. В лотерее 1000 билетов. На
- 63. Решение: Обозначим события:
- 64. Теорема сложения вероятностей
- 65. Введем обозначения для интересующих нас событий:
- 66. Вычислим вероятности этих событий по тереме сложения
- 67. Условие независимости событий Два события называются независимыми,
- 68. Вероятность события, вычисленная в предположении, что одно
- 69. События А и В независимы, если их
- 70. Условие независимости событий Аналитическая запись условия независимости событий: или
- 71. Условная вероятность события может быть получена по
- 72. Задача . Из колоды карт в 36
- 73. Решение. Вычислим “безусловные” вероятности событий:
- 74. Выводы: 1.
- 75. Задача . Зависимы или нет противоположные события?
- 76. Теорема умножения вероятностей Произведением двух или нескольких
- 77. Теорема. Вероятность произведения двух зависимых событий равна
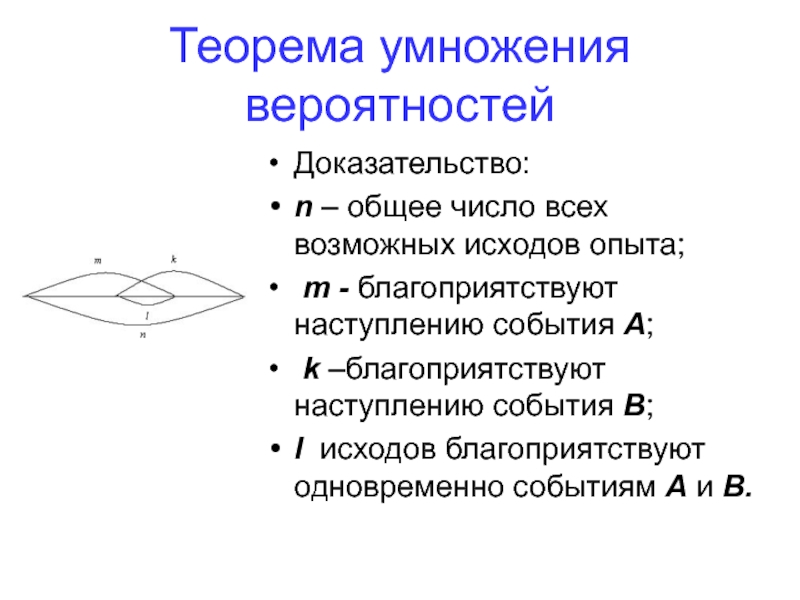
- 78. Теорема умножения вероятностей Доказательство: n – общее
- 79. Теорема умножения вероятностей Запишем вероятности этих событий:
- 80. Аналогично для трех и более событий: а)
- 81. Теорема умножения вероятностей Задача. На карточках написаны
- 82. Теорема умножения вероятностей Решение. Событие
- 83. Теорема умножения вероятностей (Т, Т, С ,
- 84. Является следствием обеих теорем – сложения и умножения вероятностей. Формула полной вероятности
- 85. Формула полной вероятности Пусть требуется определить вероятность
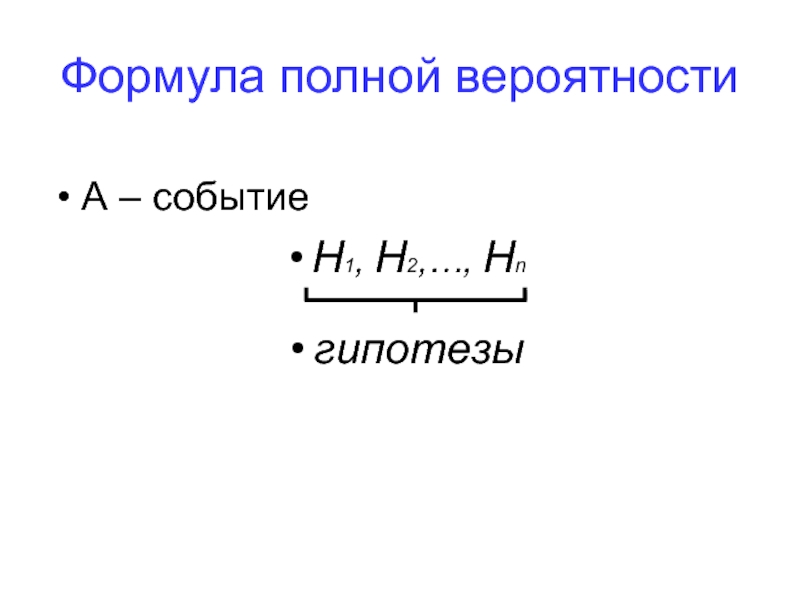
- 86. Формула полной вероятности А – событие H1, H2,…, Hn гипотезы
- 87. Формула полной вероятности Тогда вероятность события А
- 88. Формула полной вероятности Доказательство. Так как
- 89. Формула полной вероятности Так как гипотезы
- 90. Формула полной вероятности Применяя к событиям
- 91. Формула полной вероятности Задача. Имеются три одинаковые
- 92. Формула полной вероятности Решение. Событие Обозначим
- 93. Формула полной вероятности Найдем вероятность вынуть белый
- 94. Формула полной вероятности По формуле полной вероятности найдем
- 95. Формула Байеса (теорема гипотез) Является следствием теоремы умножения вероятностей и формулы полной вероятности.
- 96. Формула Байеса (теорема гипотез) Пусть имеется
- 97. Формула Байеса (теорема гипотез) Вопрос:
- 98. Формула Байеса (теорема гипотез) По теореме
- 99. Формула Байеса (теорема гипотез) Выражая P(A)
- 100. Формула Байеса (теорема гипотез) Задача. Два
- 101. Формула Байеса (теорема гипотез) Решение. p1
- 102. Формула Байеса (теорема гипотез) Условные вероятности
- 103. Формула Байеса (теорема гипотез) После опыта
- 104. Формула Байеса (теорема гипотез) Следовательно, вероятность
- 105. Испытания Бернулли. Формула Бернулли Испытания Бернулли –
Слайд 2В современном мире автоматизации производства теория вероятности(Т.В) необходима специалистам для решения
Слайд 3Под случайным событием понимается всякое явление, о котором имеет смысл говорить,
Слайд 4Основные понятия и термины ТВ
Наблюдения, опыты и измерения
Испытание - осуществление
Комплекс условий - совокупность условий, при которых выполняется каждое отдельное испытание
Слайд 5Основные понятия и термины ТВ
Результат испытания
называется событием
Событие - любой факт, который
События обозначают начальными заглавными буквами латинского алфавита:
А, В, С,… или А1, А2, А3, …
Слайд 8Примеры:
1) При подбрасывании монеты появление цифры исключает одновременное появление герба:
2) Есть
Слайд 9Основные понятия и термины ТВ
В любом опыте имеется определенное множество
Все возможные исходы опыта образуют пространство Ω элементарных событий (элеметарных исходов) этого опыта
Слайд 10Основные понятия и термины ТВ
Например,
- пространство элем. исходов опыта, связанного
- пространство элем. исходов опыта, связанного с подбрасыванием двух монет
Слайд 11Основные понятия и термины ТВ
Событие
- подпространство пространства
Событие
- подпространство пространства
Слайд 14Виды событий в ТВ
В зависимости от объективной возможности наступления:
1. Достоверное
2.
2. Случайное
или
Слайд 15Виды случайных событий
1. Простое - не может быть разложено на составляющие.
Например:
Событие
Событие - при бросании игральной кости;
Событие - при измерениях ( - случайная ошибка измерений)
Слайд 162. Сложное (составное) событие - описывается несколькими простыми событиями.
Например: событие
Виды случайных событий
Слайд 17Виды сложных событий
а) Логическая сумма (объединение) простых событий – сложное событие,
Например:
1)
2)
Слайд 18Виды сложных событий
Общепринятая запись суммы (объединения) двух событий:
что означает:
- символ логического сложения.
Слайд 20б) Логическое произведение (пересечение) простых событий - сложное событие, которое заключается
Виды сложных событий
Слайд 22Общепринятая запись произведения (пересечения):
что означает:
;
- символ логического умножения.
Виды сложных событий
Слайд 233. Равновозможные события – имеют одинаковую объективную возможность наступления при данном
Например, события:
Виды случайных событий (продолжение)
Слайд 25События
где - случ. ошибка измерений, - равновозможны при однократном измерении некоторой величины.
Виды случайных событий
Слайд 264. Единственно возможные события – такие, когда в результате испытания может
Так, в предыдущих примерах события Аi единственно возможны, равно как и события С и D
Система единственно возможных событий данного опыта образует пространство Ω элементарных событий этого опыта
Виды случайных событий
Слайд 27Виды случайных событий
5. Независимые и зависимые события – такие, у которых
Слайд 28Виды случайных событий
Система единственно возможных несовместных событий называется полной группой событий.
Так события
и при одном бросании монеты составляют полную группу событий,
равно как и события
при бросании игральной кости.
Слайд 29Виды случайных событий
6. Противоположные события – два простых или сложных события,
Событие, противоположное событию А обозначается
Слайд 31
Конечное число несовместных равновозможных событий, образующих полную группу, называются случаями, шансами,
Например, при бросании монеты возможны только два элементарных исхода: Г - “герб” и Ц - “цифра”, а при бросании игральной кости – шесть, а именно: 1, 2, 3, 4 , 5, 6.
Слайд 32
Про опыт говорят, что он сводится или не сводится к схеме
Элементарный исход называется благоприятствующим данному событию, если его осуществление влечет за собой наступление этого события.
Слайд 33Например, в опыте
выпадению герба благоприятствует один исход (Г);
В опыте
выпадению хотя бы одного герба благоприятствуют три исхода (ГГ,ГЦ,ЦГ)
Слайд 34
Численная мера объективной возможности появления события называется вероятностью события.
Вероятность –
Существует несколько определений вероятности, мы рассмотрим два из них: классическое и статистическое.
Слайд 35Классическое определение вероятности
Оно не связано с проведением опытов, т.е. вероятность события
Но при этом необходимо, чтобы возможные исходы опыта составляли схему случаев, т.е. были бы все равновозможны, несовместны, образовывали полную группу и их число должно быть конечным.
Слайд 36Классическое определение вероятности
Тогда вероятность события может быть получена по формуле
где N
M – число исходов опыта, благоприятствующих наступлению интересующего нас события.
Слайд 37Классическое определение вероятности
Согласно формулы ( I ),
При одном бросании монеты:
Р(Г)
При одном бросании игральной кости:
P(6) = 1/6;
Р{четная цифра} = 3/6 = 1/2.
Слайд 38Классическое определение вероятности
В формуле (I)
или
т.е.
Т.о. предельное числовое значение вероятности вообще есть единица.
Слайд 39Классическое определение вероятности
При
- вероятность достоверного события равна единице.
При имеем
- вероятность невозможного события равна нулю.
При имеем
- вероятность случайного события может изменяться в пределах от нуля до единицы, не достигая их.
Слайд 40Классическое определение вероятности
Обозначим
Тогда , т.к.
,
т.е. сумма вероятностей противоположных событий равна единице.
Слайд 41Классическое определение вероятности
Недостаток: опыты редко сводятся к схеме случаев и чаще
Поэтому формула ( I ) имеет ограниченное (но достаточно широкое ) применение.
Слайд 42Статистическое определение вероятности
Связано с проведением опытов и с понятием относительной частоты
,
где n – число испытаний;
k – число появлений события в этих испытаниях (абсолютная частота).
Слайд 43Статистическое определение вероятности
Свойство устойчивости относительной частоты в опытах отражено в теореме
где ε и δ - бесконечно малые числа.
Или
Слайд 44На основании теоремы Бернулли : вероятность – это предел, к которому
Статистическое определение вероятности
Слайд 45
Практически статистическая вероятность может быть найдена по приближенной формуле
Статистическое определение вероятности
Слайд 46Недостаток - необходимость выполнения бесконечного числа опытов или достаточно большого их
Статистическое определение вероятности
Слайд 47Формулы ( I ) и ( II ) выражают прямые способы
Они являются главными, но не основными.
Основными следует считать косвенные способы.
Слайд 48Косвенные способы вычисления вероятностей
Позволяют по известным вероятностям одних событий вычислять вероятности
Это сводит необходимый эксперимент к минимуму.
Вся ТВ есть система таких косвенных способов.
Слайд 49К ним относятся:
- теоремы (аксиомы) ТВ;
- формула полной вероятности;
- формула Байеса;
-
- формула использования вероятности противоположного события и др.
Косвенные способы вычисления вероятностей
Слайд 511. В урне 3 белых и 9 черных шаров. Из урны
Решение:
Количество всех возможных результатов n=3+9=12.
Опытов, в результате которых может быть вынут белый шар m=3.
Ответ: 0, 25
Слайд 522. Брошена игральная кость. Какова вероятность событий: А- выпало 1 очко;
Решение:
Количество всех возможных результатов n=6 (все грани).
а) Количество граней, на которых всего 1 очко m=1:
б) количество граней, на которых всего 2 очка m=1:
Ответ: и
Слайд 533. Брошены 2 игральные кости. Какова вероятность событий: А- выпадения в
Решение:
Получили, что возможно n=36 результатов испытаний
Слайд 56Основные теоремы ТВ
Используются для вычисления вероятностей сложных событий.
Их две –
Строго могут быть доказаны только для событий, сводящихся к схеме случаев.
Для других событий применяются как аксиомы, принципы, постулаты.
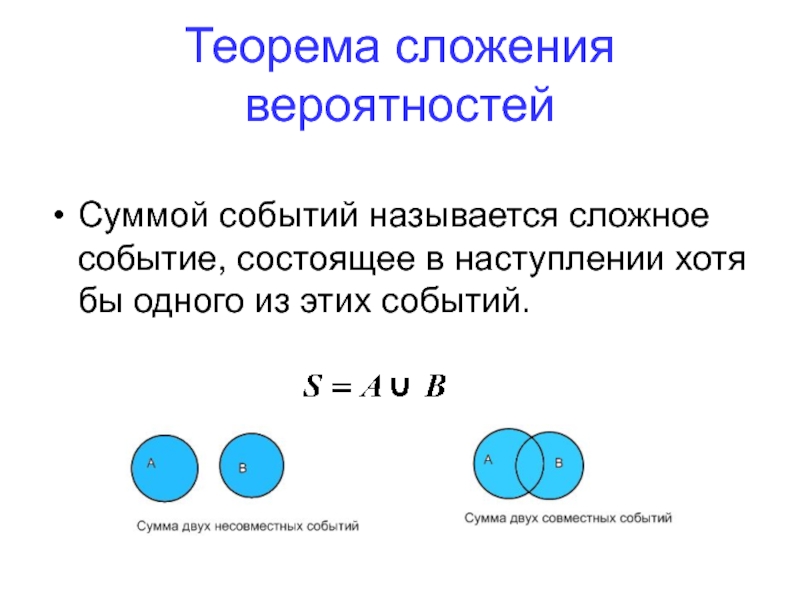
Слайд 57Теорема сложения вероятностей
Суммой событий называется сложное событие, состоящее в наступлении хотя
Слайд 58Теорема: Вероятность суммы двух или нескольких совместных событий равна сумме вероятностей
Теорема сложения вероятностей
Слайд 59Теорема сложения вероятностей
Доказательство:
n – общее число всех возможных исходов опыта;
k –благоприятствуют наступлению cобытия В;
l исходов благоприятствуют одновременно событиям А и В.
Слайд 60
Очевидно, что событию благоприятствуют все исходов.
Запишем вероятности этих событий:
Или
Ч.т.д.
Теорема сложения вероятностей
Слайд 61Теорема сложения вероятностей
Для несовместных событий l = 0.
В этом случае
т.е. вероятность
Следствие. Сумма вероятностей событий A1, A2,…,An , образующих полную группу, равна единице - как вероятность достоверного события:
Слайд 62Задача 1. В лотерее 1000 билетов. На один билет падает выигрыш
а) не менее 20 рублей;
б) любую сумму денег?
Теорема сложения вероятностей
Слайд 63Решение: Обозначим события:
Найдем вероятности этих простых событий по формуле :
Теорема сложения
Слайд 65Введем обозначения для интересующих нас событий:
- сумма 3-х несовместных событий;
- сумма
Теорема сложения вероятностей
Слайд 66Вычислим вероятности этих событий по тереме сложения вероятностей несовместных событий:
Теорема сложения
Слайд 67Условие независимости событий
Два события называются независимыми, если вероятность появления одного из
Слайд 68Вероятность события, вычисленная в предположении, что одно или несколько событий к
- условная вероятность события А относительно события B;
- условная вероятность события В относительно события A.
Условие независимости событий
Слайд 69События А и В независимы, если их условные вероятности равны “безусловным”,т.е.
Условие независимости событий
Слайд 71Условная вероятность события может быть получена по формуле
Ясно, что если
Условие независимости событий
Слайд 72Задача . Из колоды карт в 36 листов берут наугад одну
Определить их парную независимость (или зависимость).
Условие независимости событий
Слайд 73Решение. Вычислим “безусловные” вероятности событий:
Вычислим необходимые условные вероятности:
Условие независимости событий
Слайд 74Выводы:
1.
2. , следовательно, события А и С зависимы.
3. , следовательно, события В и С зависимы.
Условие независимости событий
Слайд 75Задача . Зависимы или нет противоположные события?
Решение. Запишем условие независимости для
А - случайное событие.
Его вероятность
Но , т.к. и не совместны в одном испытании.
Вывод: события зависимы, т.к.
Условие независимости событий
.
.
Слайд 76Теорема умножения вероятностей
Произведением двух или нескольких событий называется сложное событие, состоящее
Слайд 77Теорема. Вероятность произведения двух зависимых событий равна произведению безусловной вероятности одного
Теорема умножения вероятностей
Слайд 78Теорема умножения вероятностей
Доказательство:
n – общее число всех возможных исходов опыта;
k –благоприятствуют наступлению cобытия В;
l исходов благоприятствуют одновременно событиям А и В.
Слайд 79Теорема умножения вероятностей
Запишем вероятности этих событий:
Условная вероятность события В:
Подставив все эти
что и подтверждает правильность доказываемой формулы.
Слайд 80Аналогично для трех и более событий:
а)
б)
Для независимых событий А и В:
Поэтому для независимых событий
Теорема умножения вероятностей
Слайд 81Теорема умножения вероятностей
Задача. На карточках написаны буквы Т, Т, С и
Определить вероятность того, что в порядке появления букв получится слово ТОСТ.
Слайд 82Теорема умножения вероятностей
Решение.
Событие по определению есть
Вскрытые карточки обратно не возвращаются, поэтому элементарные события, образующие событие В зависимы (изменяются условия опыта).
Слайд 83Теорема умножения вероятностей
(Т, Т, С , О)
Поэтому для решения задачи применим
Тогда
Слайд 84Является следствием обеих теорем – сложения и умножения вероятностей.
Формула полной вероятности
Слайд 85Формула полной вероятности
Пусть требуется определить вероятность события А, которое может произойти
H1, H2,…, Hn,
образующих полную группу и называемых гипотезами.
Слайд 87Формула полной вероятности
Тогда вероятность события А вычисляется как
т.е.как сумма произведений
Слайд 88Формула полной вероятности
Доказательство.
Так как гипотезы
Слайд 89Формула полной вероятности
Так как гипотезы
Тогда по теореме сложения вероятностей:
Слайд 90Формула полной вероятности
Применяя к событиям
,
что и требовалось доказать.
Слайд 91Формула полной вероятности
Задача. Имеются три одинаковые с виду урны. В первой
Некто подходит к одной из урн и вынимает из нее один шар.
Найти вероятность того, что этот шар белый.
Слайд 92Формула полной вероятности
Решение.
Событие
Обозначим события-гипотезы:
1-я урна 2-я
H1 H2 H3
Т.к. выбор урны происходит случайно, наугад, то вероятность каждой гипотезы
Слайд 93Формула полной вероятности
Найдем вероятность вынуть белый шар из 1-й урны, т.е.
затем – из 2-й:
и, наконец, из 3-й:
Слайд 95Формула Байеса
(теорема гипотез)
Является следствием теоремы умножения вероятностей и формулы полной
Слайд 96Формула Байеса
(теорема гипотез)
Пусть имеется полная группа несовместных гипотез:
Пусть вероятности этих гипотез до опыта известны и равны
Пусть проведен опыт, в результате которого наступило некоторое событие А
Слайд 97Формула Байеса
(теорема гипотез)
Вопрос: как следует изменить вероятности гипотез в
По существу нужно найти «новую» (условную) вероятность
для каждой гипотезы.
Слайд 99Формула Байеса
(теорема гипотез)
Выражая P(A) с помощью формулы полной вероятности, имеем
Формула
Слайд 100Формула Байеса
(теорема гипотез)
Задача. Два стрелка стреляют в одну мишень, делая
Вероятность попадания в мишень для первого стрелка равна 0.8, а для второго 0.4.
После стрельбы в мишени обнаружена пробоина.
Найти вероятность того, что эта пробоина принадлежит первому стрелку.
Слайд 101Формула Байеса
(теорема гипотез)
Решение. p1 = 0.8, p2 = 0.4
До
. Их вер-ти:
Слайд 102Формула Байеса
(теорема гипотез)
Условные вероятности наблюденного события
А = {пробоина}
при этих гипотезах
Слайд 103Формула Байеса
(теорема гипотез)
После опыта гипотезы H 1 и Н 2
Вероятности гипотез H3 и Н4 будут равны:
Слайд 104Формула Байеса
(теорема гипотез)
Следовательно, вероятность того, что пробоина принадлежит первому стрелку,
Слайд 105Испытания Бернулли.
Формула Бернулли
Испытания Бернулли – это повторные многократные, независимые испытания с
Классический пример – многократное бросание монеты.