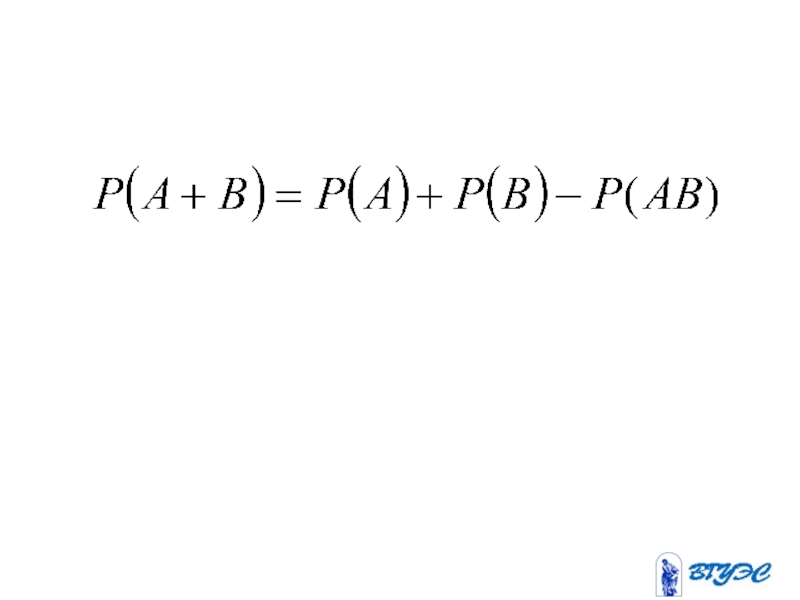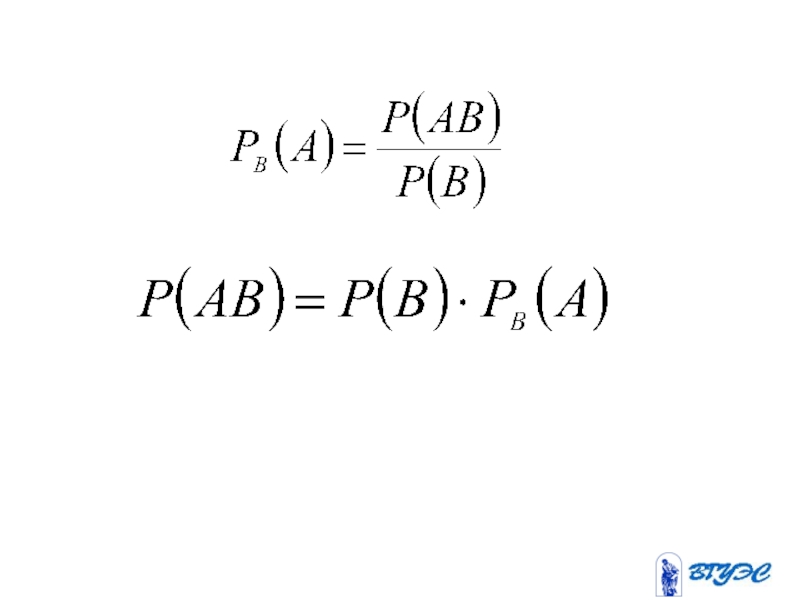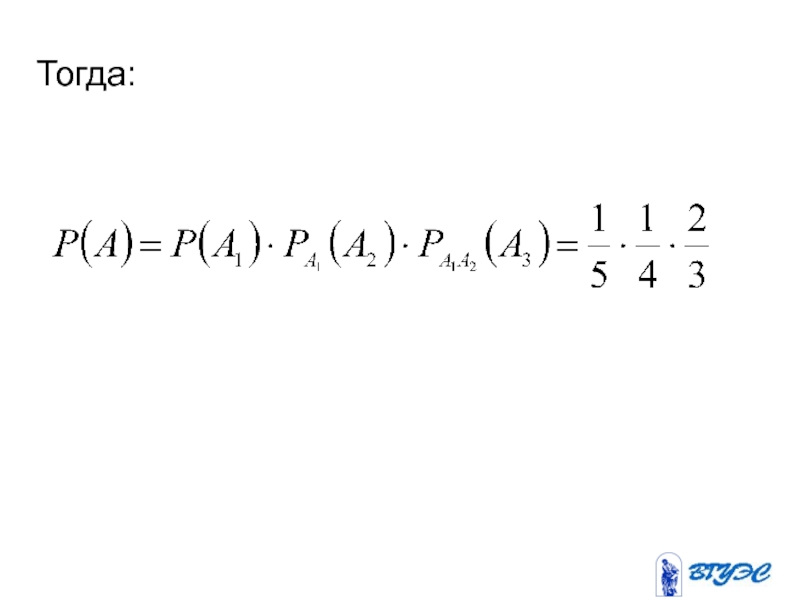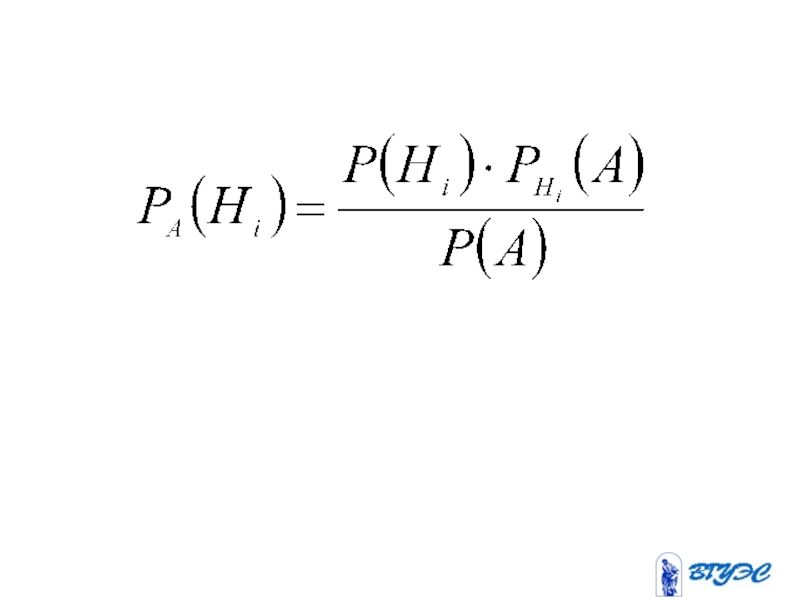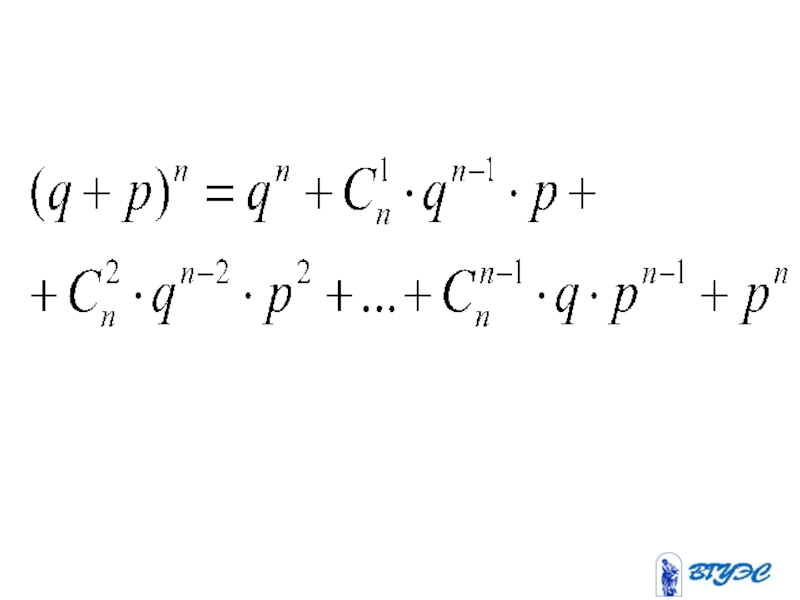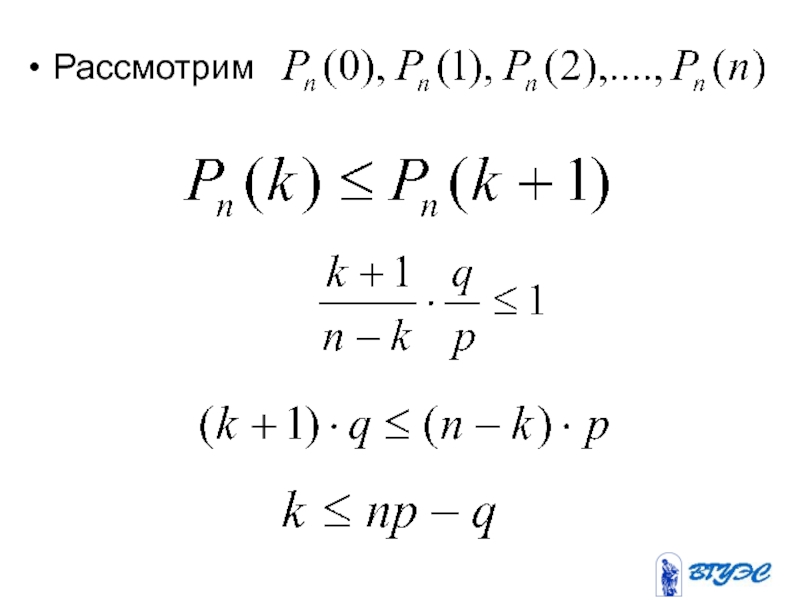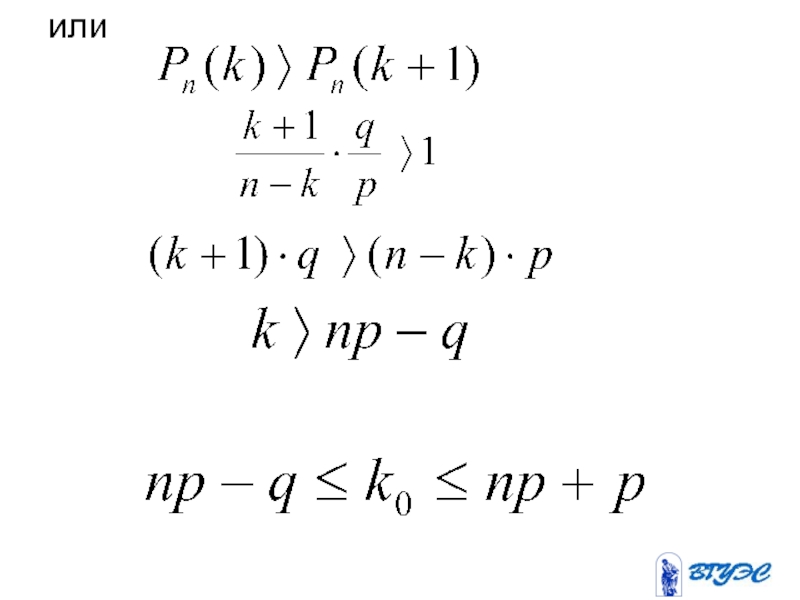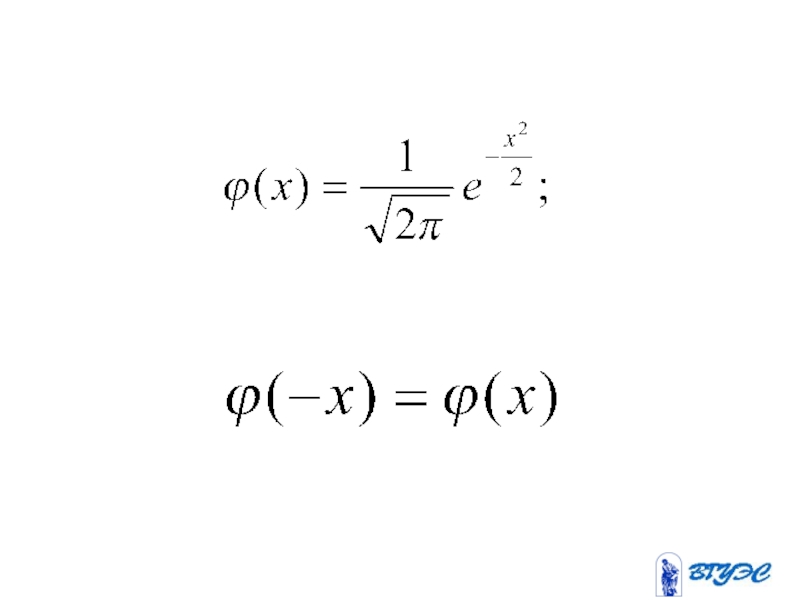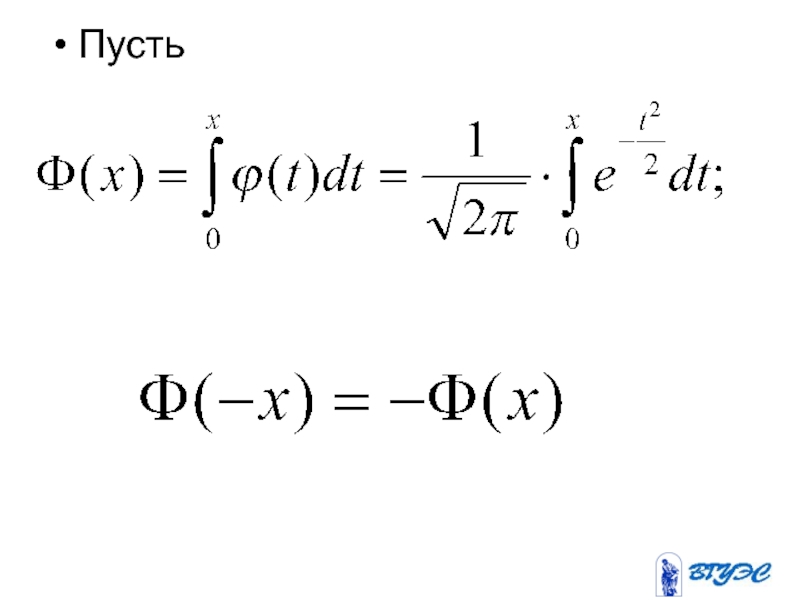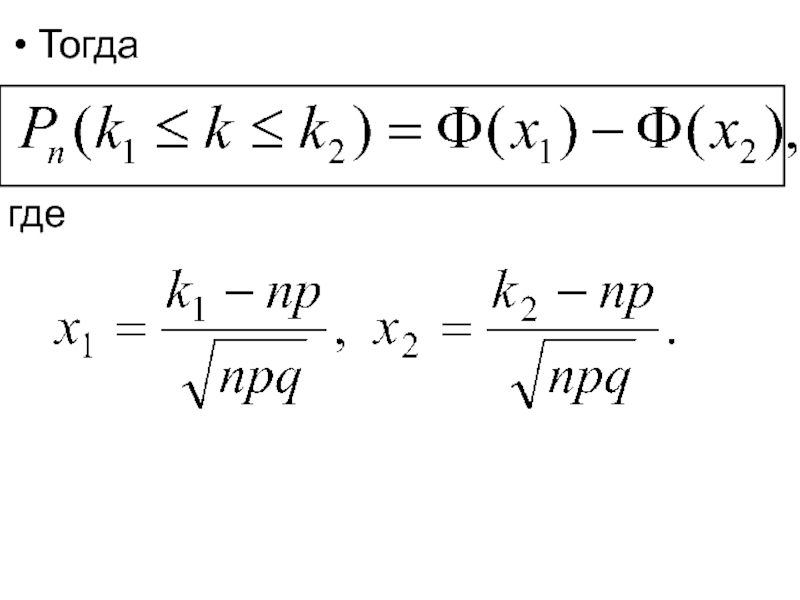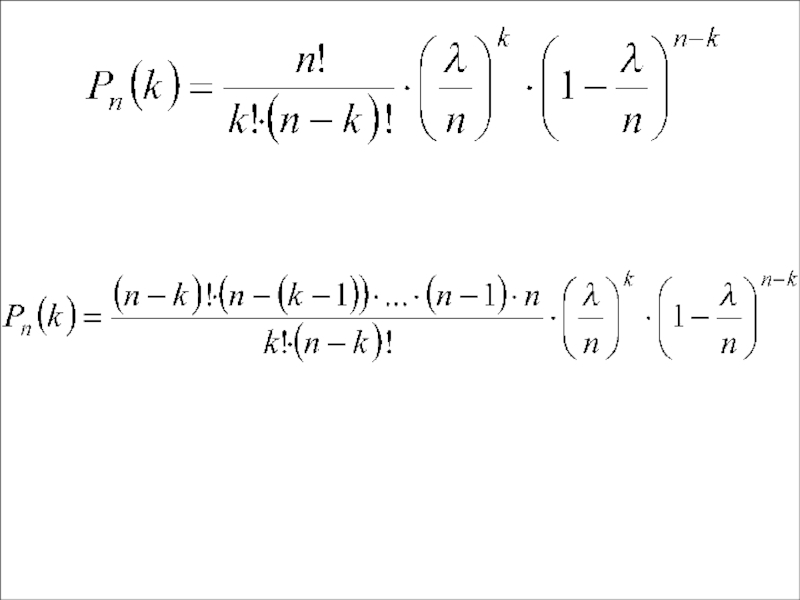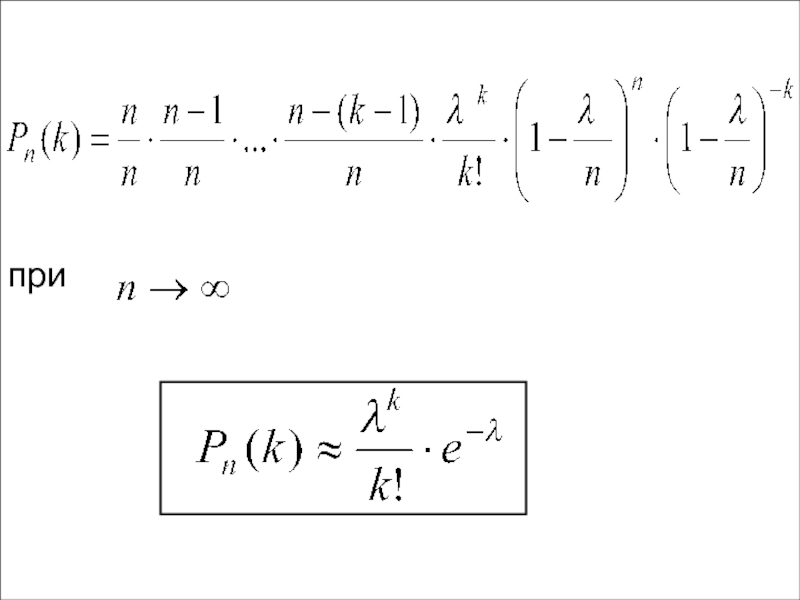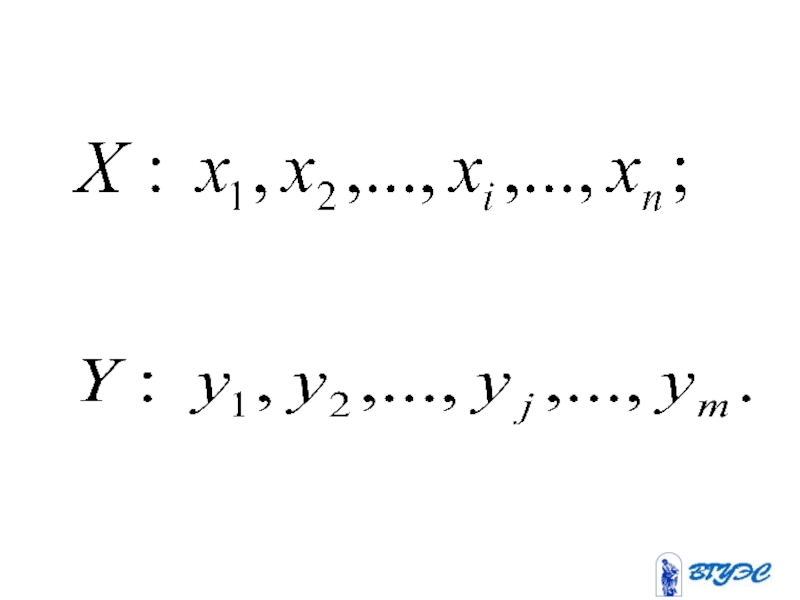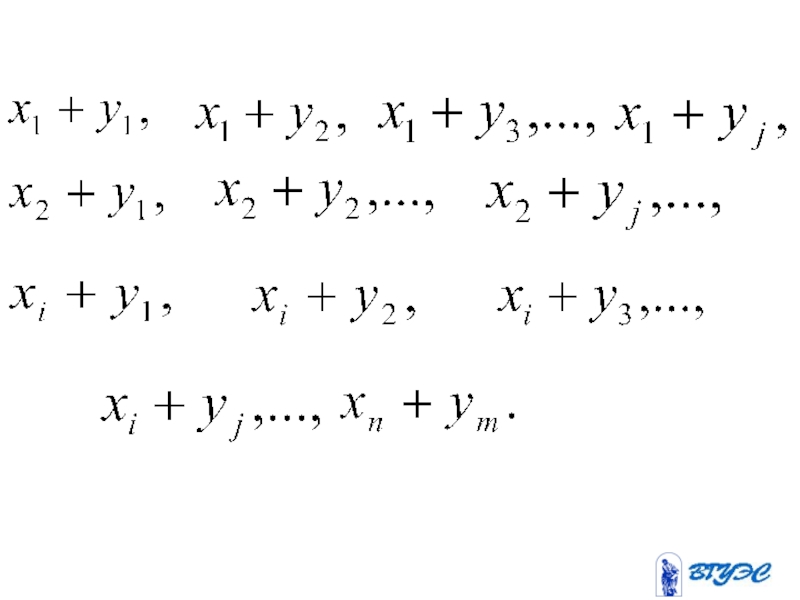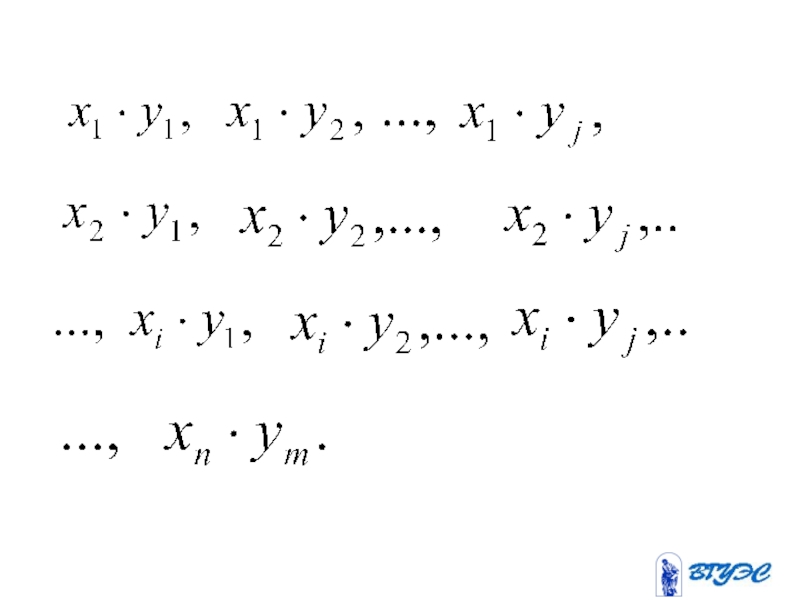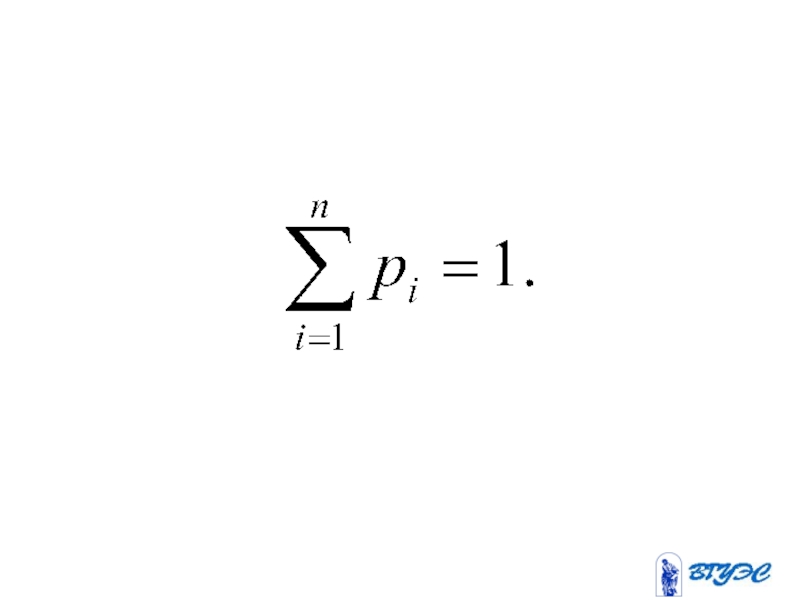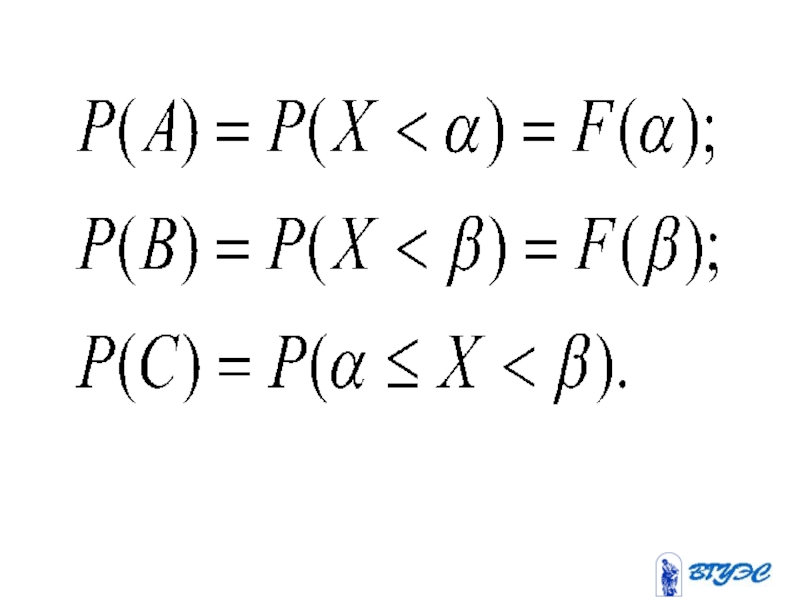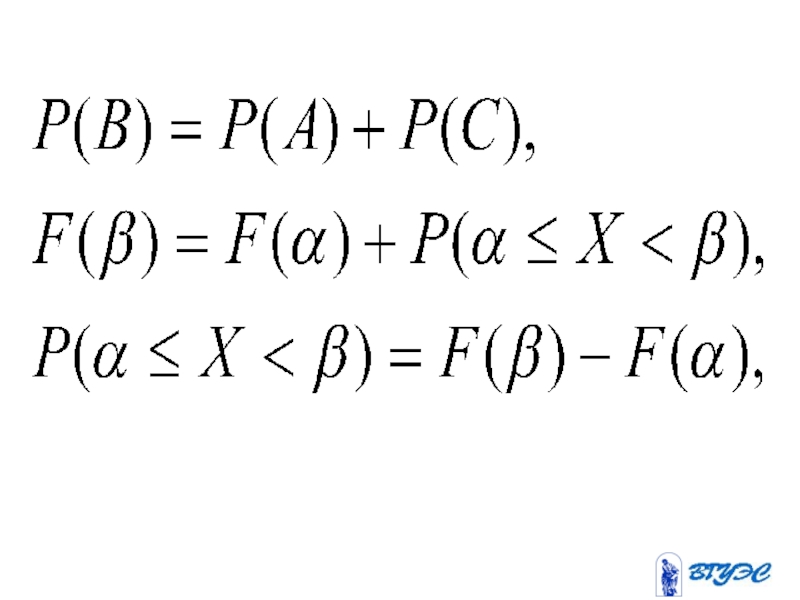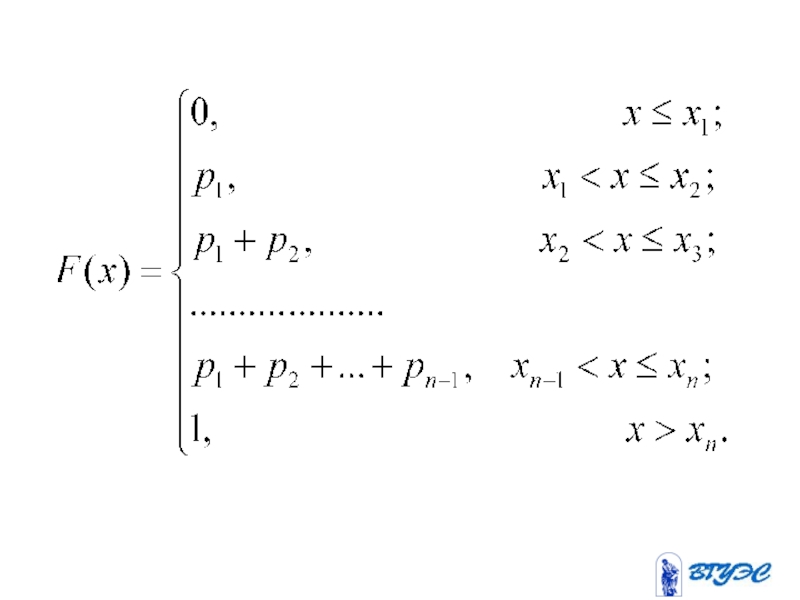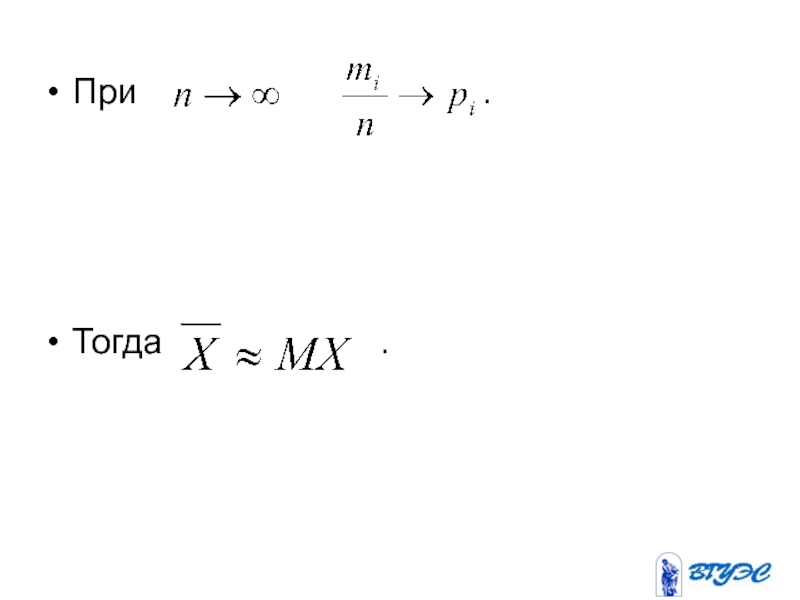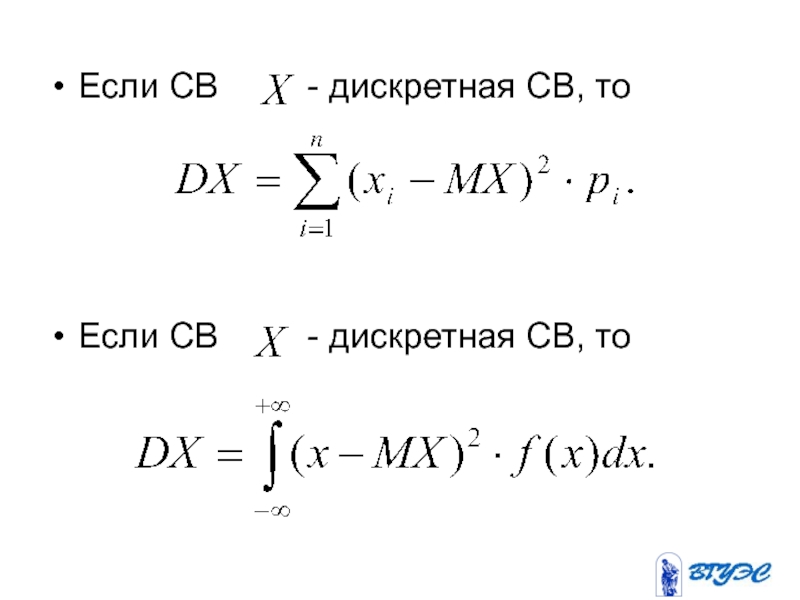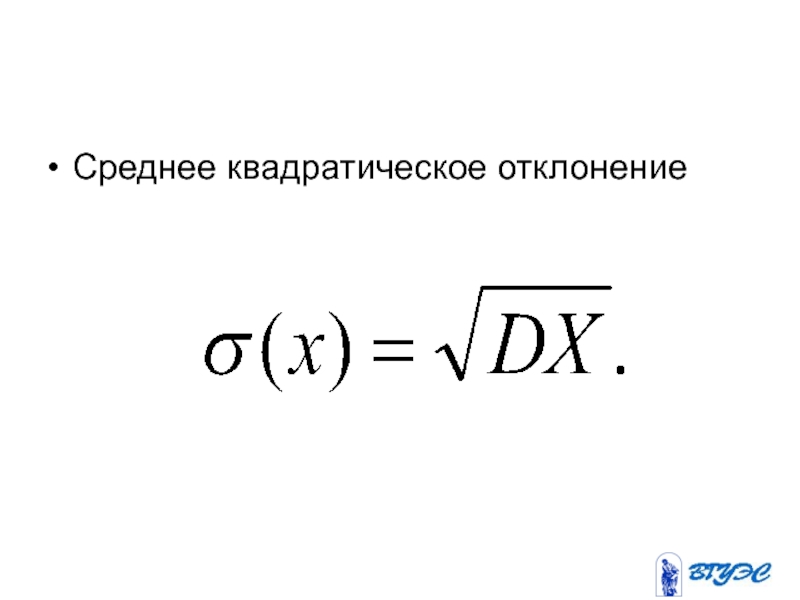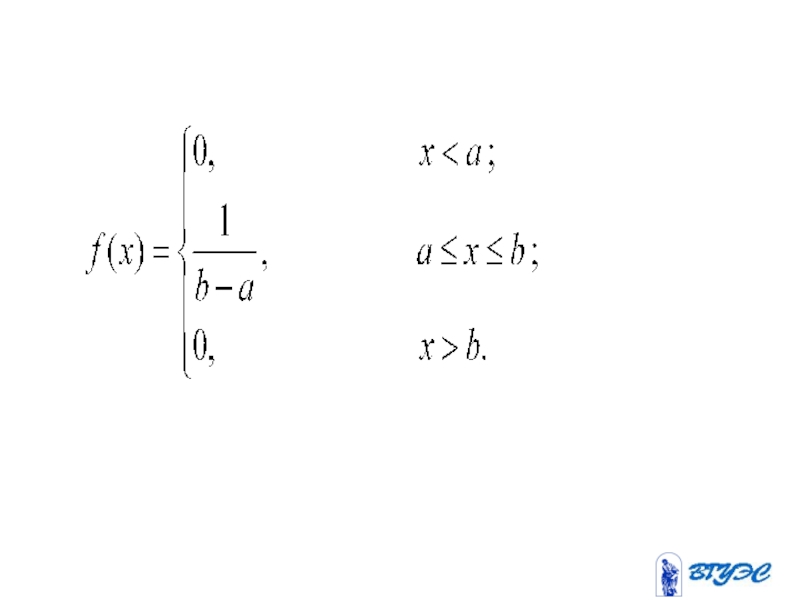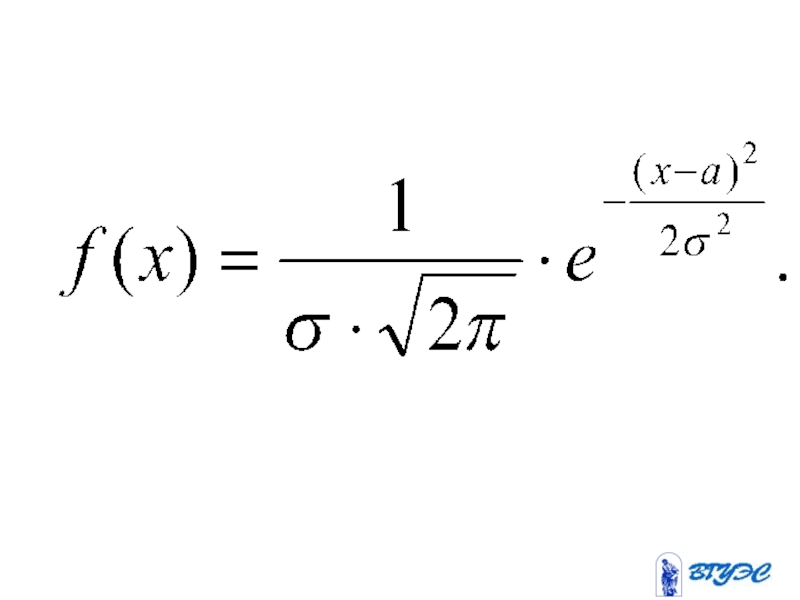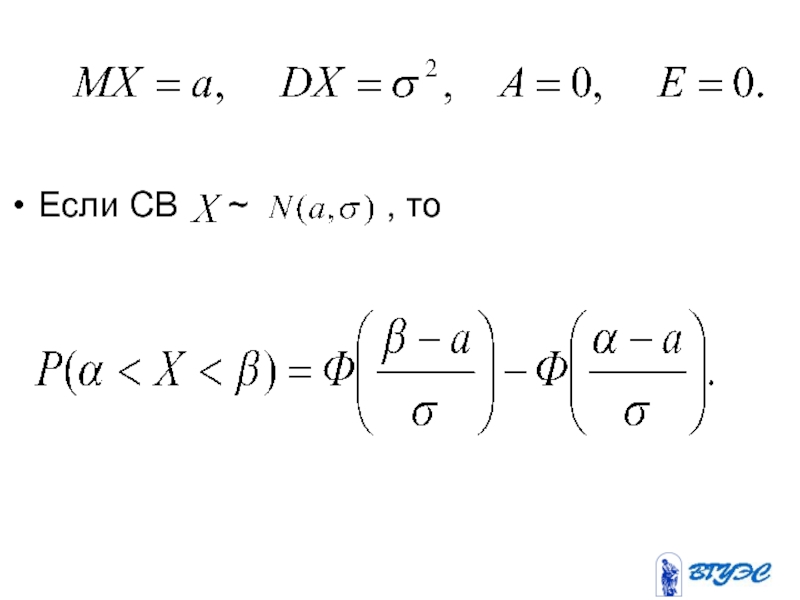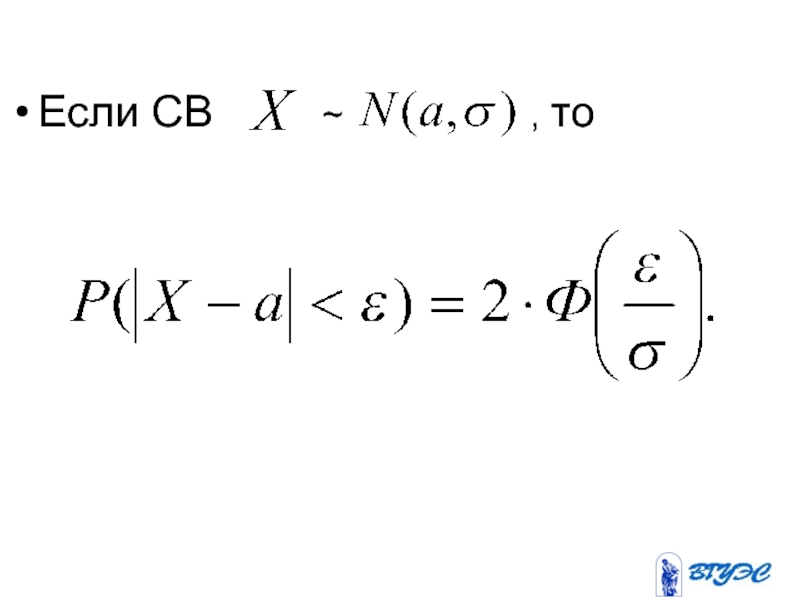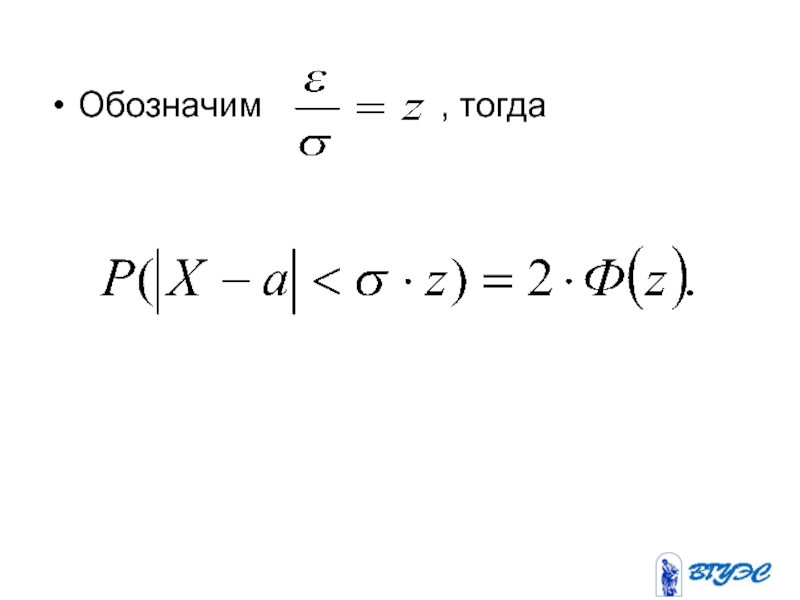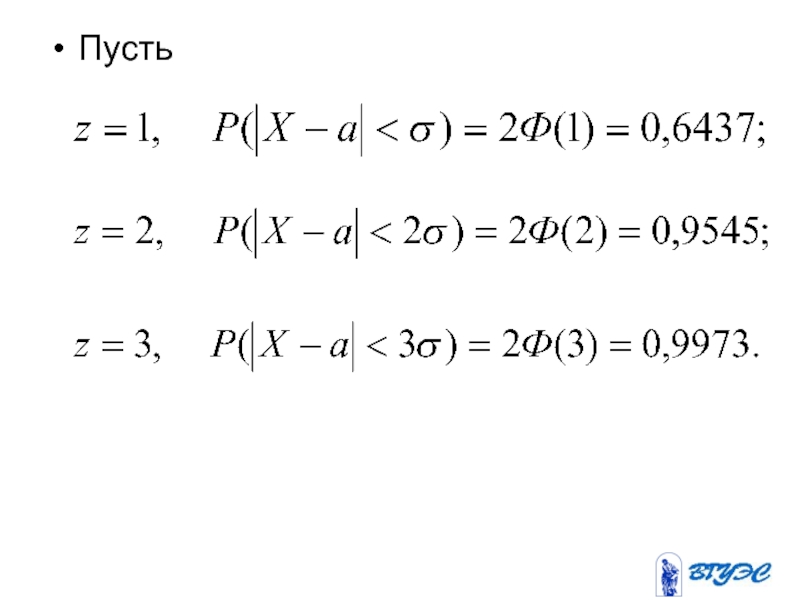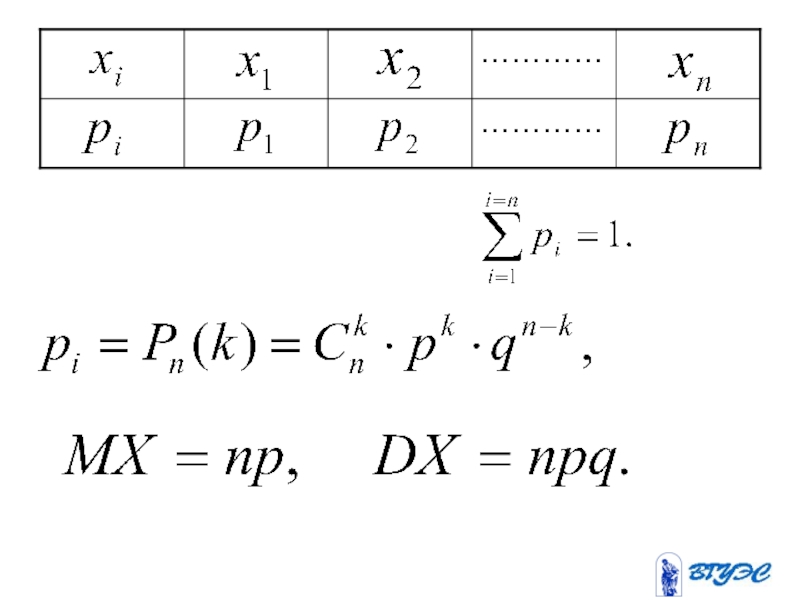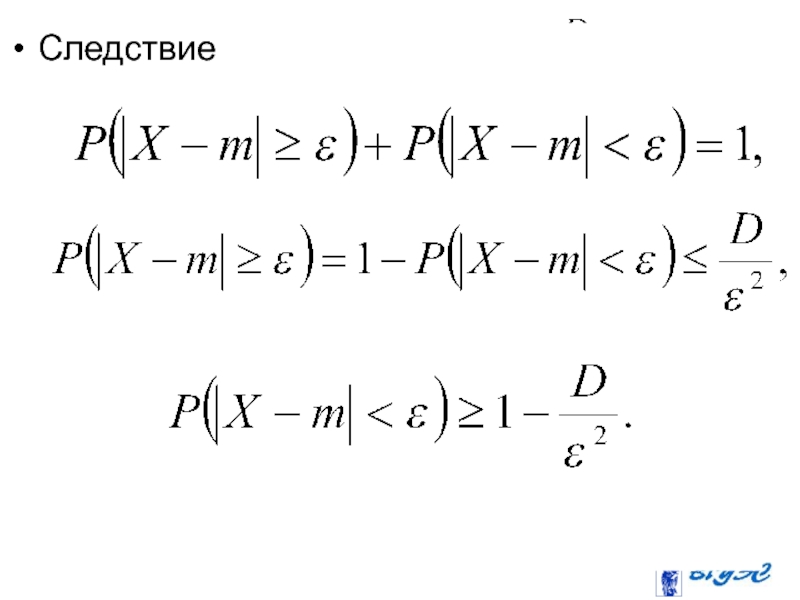- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика презентация
Содержание
- 1. Теория вероятностей и математическая статистика
- 2. Список литературы 1. Н.Н. Одияко, Н.Ю.
- 3. 4. В.Е. Гмурман. Теория вероятностей и математическая
- 4. Основные понятия комбинаторики
- 5. Правило умножения
- 6. Пусть требуется выполнить одно за другим
- 7. Правило сложения
- 8. Если два действия взаимно исключают друг друга
- 9. Опр. Последовательность
- 10. Опр. Размещением из
- 11. Опр. Перестановками из элементов называется любое
- 12. Опр. Сочетанием из элементов по
- 13. СЛУЧАЙНЫЕ СОБЫТИЯ И ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 14. Опр. Испытание (опыт, эксперимент)- выполнение определенного комплекса
- 15. Опр. Событие называется случайным по отношению к
- 16. Определения.
- 17. 4. События называются несовместными,
- 18. 6. События называются единственно
- 19. 7. Несколько событий образуют полную группу,
- 20. «Статистическое определение» вероятности случайного события
- 21. Опр. Пусть при - кратном
- 22. Опр.
- 23. Если событие
- 24. Комбинация событий
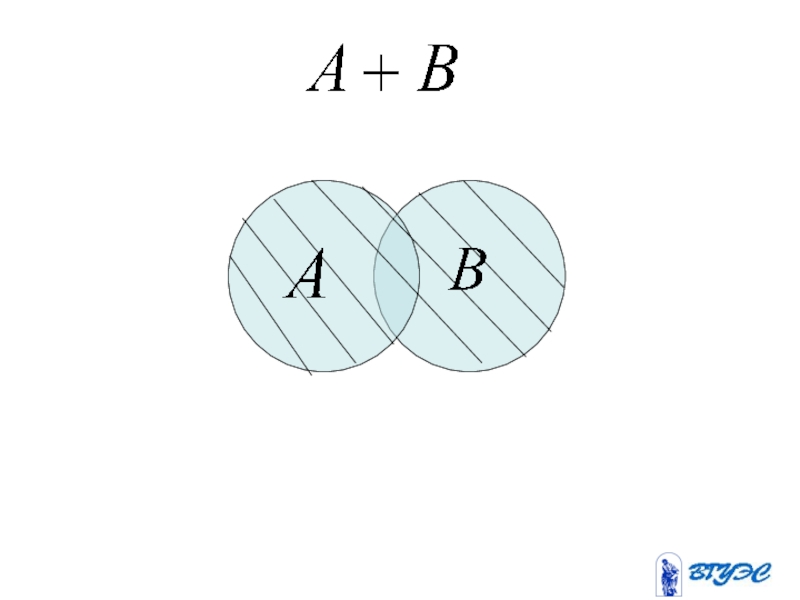
- 25. Опр. Суммой событий и
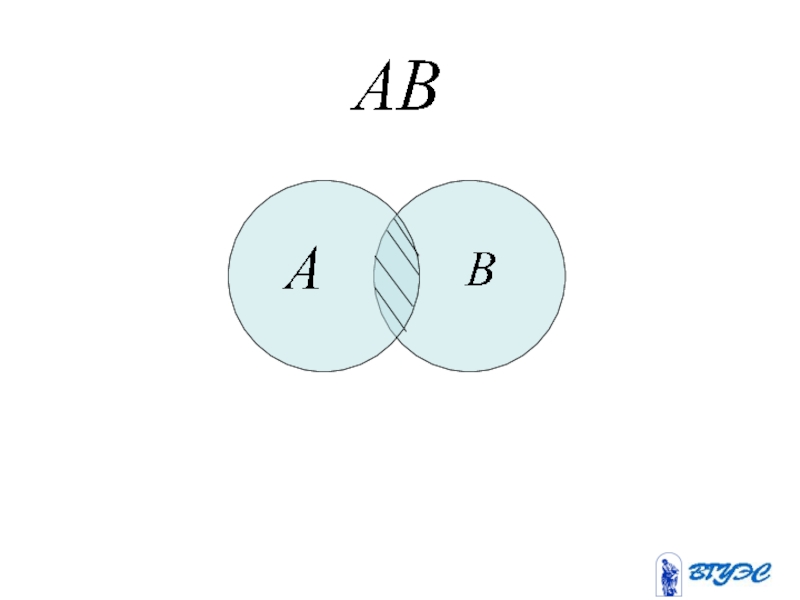
- 27. Опр. Произведением событий
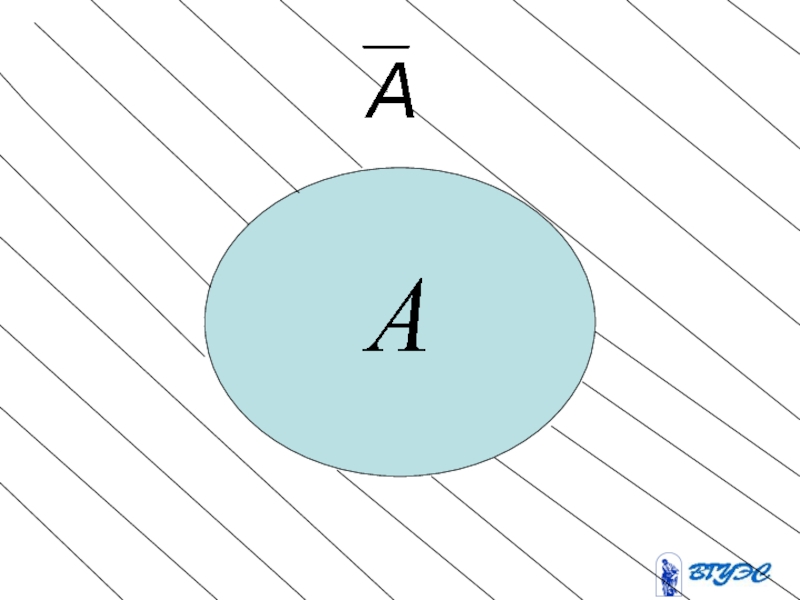
- 29. Опр. Событие называется противоположным
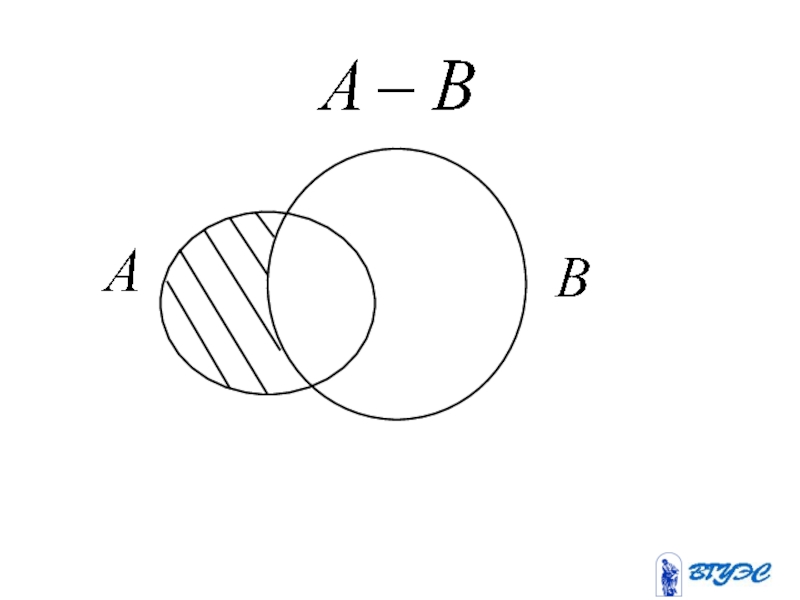
- 31. Опр. Разностью
- 33. Правило сложения вероятностей.
- 34. Если события несовместны, то вероятность
- 35. Следствие.
- 37. Классический способ подсчета вероятности
- 38. Эту формулу применяют в тех случаях, когда
- 40. Вероятность события равна отношению числа элементарных
- 41. Геометрическое определение вероятности
- 42. Опр. Геометрической вероятностью события
- 43. Условная вероятность
- 44. Опр. Условной вероятностью события
- 46. Пример. Слово “лотос” составлено из одинаковых букв-
- 47. Представим событие в виде:
- 48. Тогда:
- 49. Независимые события
- 50. Опр. События называются независимыми, если наступление
- 51. ЗАМЕЧАНИЯ. Для совместных событий: Для
- 52. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
- 53. Предположим, что событие
- 54. ФОРМУЛА БАЙЕСА
- 55. Эта формула решает следующую задачу: пусть произведен
- 57. Формула Бернулли
- 58. где -
- 59. Замечание. Формулу Бернулли используют при
- 61. т.к.
- 62. Событие произойдет: а)
- 63. в) более
- 64. Наиболее вероятное число успехов
- 65. Рассмотрим
- 66. или
- 67. Вероятность при больших значениях
- 68. Локальная приближенная формула Лапласа ( -велико)
- 71. Интегральная формула Лапласа
- 72. Формула позволяет найти
- 73. Пусть
- 74. Свойства интегральной функции Лапласа 1)
- 75. Тогда где
- 76. Формулы применяются при но при
- 77. Вероятность того, что частота наступления соб.
- 78. Приближенная формула Пуассона
- 79. велико,
- 80. Док-во: Воспользуемся формулой Бернулли
- 82. при
- 83. Формулу Пуассона можно использовать если
- 84. Случайные величины
- 85. Опр. Случайной называется величина, которая в
- 86. Опр. Дискретной случайной величиной называют
- 87. Опр. Непрерывной случайной величиной называют
- 88. Случайные величины:
- 89. Операции над случайными величинами.
- 91. Определение. Суммой
- 93. Опр. Произведением случайных величин и
- 95. Опр. Произведением
- 96. Закон распределения случайной величины
- 97. Опр. Законом распределения дискретной случайной
- 98. Закон распределения случайной величины можно задать, как и функцию: табличным, графическим и аналитическим способами.
- 99. Опр. Две случайные величины называются
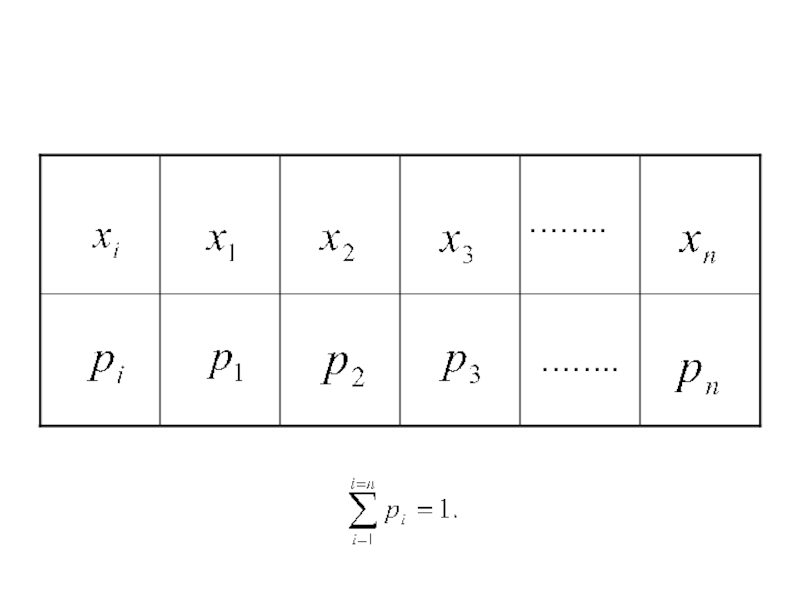
- 100. Табличный способ
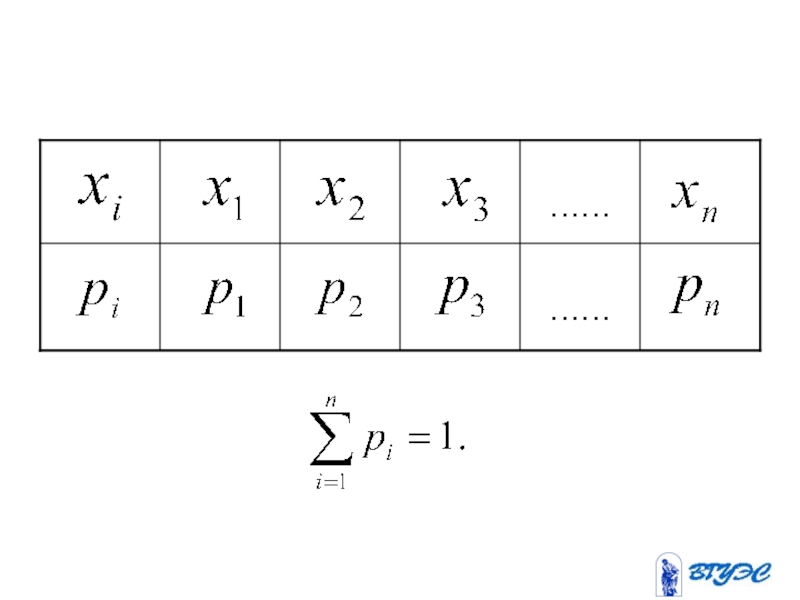
- 101. Ряд распределения случайной величины
- 102. Пусть
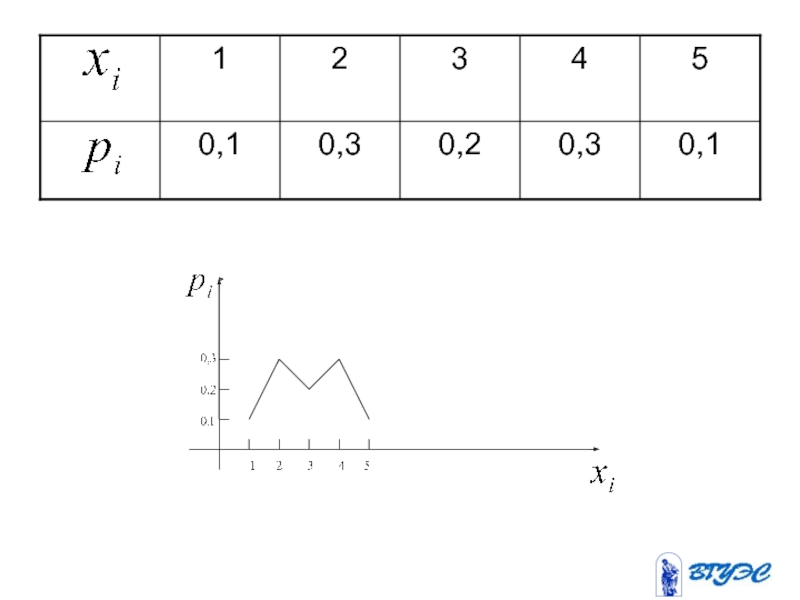
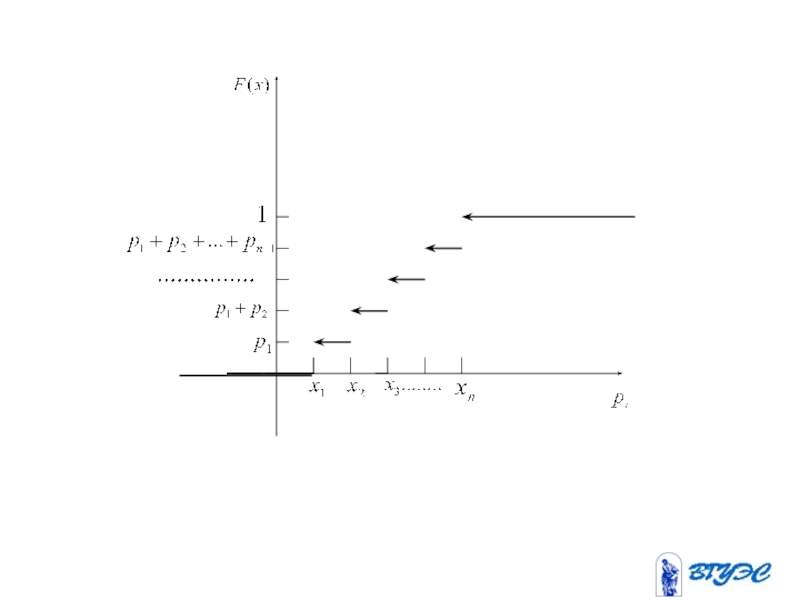
- 105. Графический способ
- 106. Многоугольник распределения
- 108. Аналитический способ
- 109. Функция распределения вероятностей
- 110. Опр. Функцией распределения вероятностей случайной величины
- 111. Свойства функции распределения.
- 112. 1.
- 115. Т.к. Отсюда - неубывающая.
- 116. 3. Если
- 117. Если - дискретная
- 118. …………………………………………...........
- 121. Плотность распределения вероятностей
- 122. Пусть -непрерывная случайная величина.
- 123. Обозначим
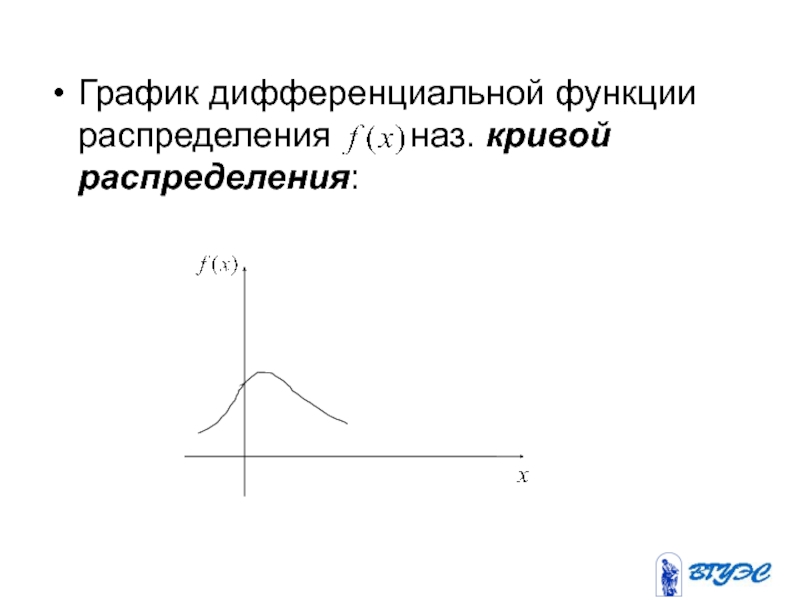
- 124. Опр. Дифференциальной функцией распределения или
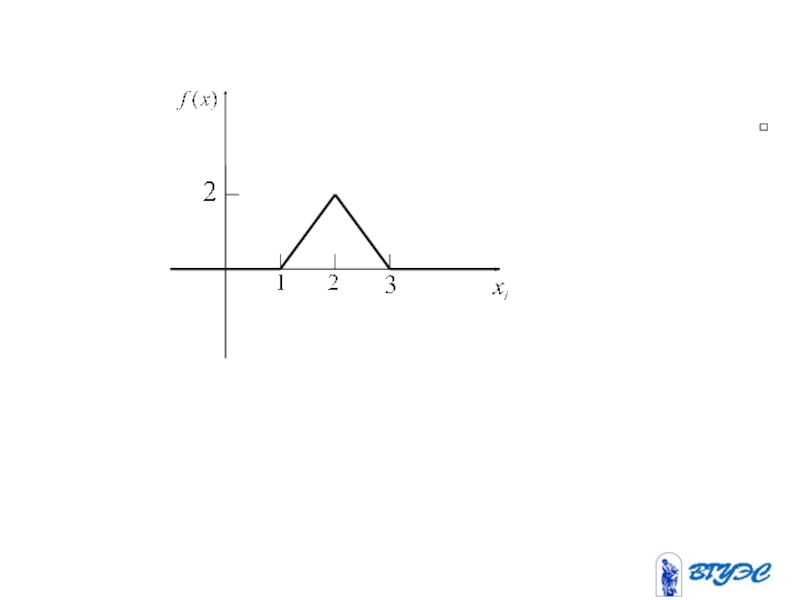
- 125. График дифференциальной функции распределения наз. кривой распределения:
- 126. Свойства плотности распределения вероятности.
- 127. 1.Для 2.Для
- 128. Числовые характеристики случайных величин.
- 129. Математическое ожидание.
- 131. Опр. Математическим ожиданием дискретной случайной величины
- 132. Пусть случайная величина приняла
- 133. При
- 134. Опр. Математическим ожиданием непрерывной случайной величины
- 135. Свойства математического ожидания
- 136. 1. 2. 3.Если
- 137. Пример 1.
- 138. Пример 2.
- 141. Дисперсия Опр. Математическое ожидание квадрата отклонения
- 142. Если СВ -
- 143. Среднее квадратическое отклонение
- 144. Свойства дисперсии 1. 2. 3. 4. 5.
- 145. Опр. СВ
- 146. Опр. Начальным моментом
- 147. Опр. Коэффициентом асимметрии
- 148. Опр. Эксцессом наз-ся величина
- 149. Виды распределения
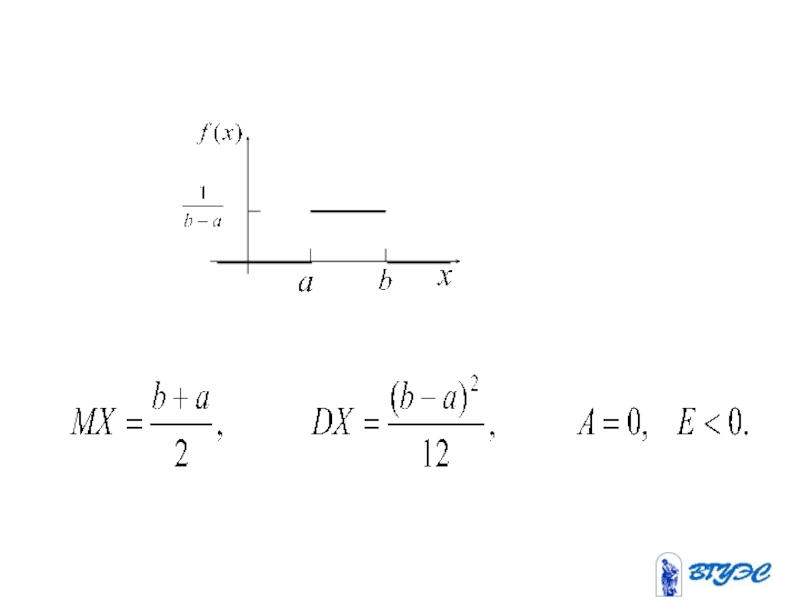
- 150. Равномерное распределение
- 153. Нормальное распределение
- 155. Если СВ
- 156. Если СВ
- 157. Обозначим , тогда
- 158. Пусть
- 159. Правило «трёх сигм»: если СВ распределена по
- 160. Биномиальное распределение
- 162. Распределение Пуассона
- 164. Закон больших чисел
- 165. Неравенство Чебышева
- 166. Пусть имеется СВ с
- 167. Если СВ ,
- 168. Следствие
- 169. Теорема Чебышева
- 170. Пусть имеется бесконечная последовательность независимых случайных
Слайд 2Список литературы
1. Н.Н. Одияко, Н.Ю. Голодная. Теория
вероятностей. Учебное пособие.
2.
одномерной выборки.
3. Н.Ю. Голодная, Н.Н. Одияко.
Математическая статистика. Теория
корреляции в расчетах. Часть2.
Слайд 34. В.Е. Гмурман. Теория вероятностей и
математическая статистика.
5. В.Е. Гмурман. Руководство к
задач по теории вероятностей и
математической статистике.
Слайд 6Пусть требуется выполнить одно за
другим какие-то действия.
первое действие можно выполнить
способом, второе действие -
способами, третье - способами и т.д.
до действия, которое можно
выполнить способами, то все
действий вместе быть выполнены
могут быть выполнены
способами.
Слайд 8Если два действия взаимно исключают друг друга , причём одно из
Это правило распространяется на любое конечное число действий.
Слайд 9
Опр. Последовательность
элементов называется
упорядоченной, если порядок
следования элементов в ней задан
Слайд 10
Опр. Размещением из элементов по
Слайд 11Опр. Перестановками из элементов называется любое упорядоченное множество,
Слайд 12Опр. Сочетанием из элементов по элементов называется любое подмножество
Слайд 14Опр. Испытание (опыт, эксперимент)-
выполнение определенного комплекса
условий, в которых наблюдается то
иное явление, фиксируется тот или иной
результат
Слайд 15Опр. Событие называется случайным по отношению к данному испытанию (опыту), если
Событие обозначается:
Слайд 16 Определения.
1.Событие , которое
2.Событие, которое в результате опыта никогда не наступит называется невозможным.
3. Если одновременно одно событие влечет за собой другое и наоборот, такие события называются равносильными.
Слайд 17 4. События называются несовместными,
если наступление одного из
наступление любого другого.
5. События называются
равновозможными, если в результате
испытания по условиям симметрии ни одно
из этих событий не является объективно
более возможным.
Слайд 18 6. События называются
единственно возможными, если появление в
результате испытания
одного из них является практически
достоверным событием.
Слайд 197. Несколько событий образуют
полную группу, если они являются
единственно возможными и
несовместными исходами испытания.
Это означает, что в результате
испытания обязательно должно
произойти одно и только одно из этих
событий.
Слайд 21Опр. Пусть при - кратном повторении опыта
Слайд 22 Опр.
Вероятность случайного события – это
связанное
число, около которого колеблется частота
наступления этого события в длинных
сериях опытов.
Слайд 25
Опр. Суммой событий и называется событие
Слайд 27
Опр. Произведением событий и
называется событие
одновременном появлении этих
событий.
Слайд 29
Опр. Событие называется противоположным событию , если
Слайд 31Опр. Разностью двух событий
и называется событие, которое
состоится, если событие произойдет, а
событие не произойдет.
Слайд 38Эту формулу применяют в тех случаях, когда исходы некоторого испытания образуют
Такие исходы называются элементарными исходами
Слайд 40Вероятность события равна отношению
числа элементарных исходов,
благоприятных для этого события,
общему числу элементарных исходов.
Слайд 42Опр. Геометрической вероятностью
события называется отношение меры
области благоприятствующей появлению
события
Слайд 44Опр. Условной вероятностью
события относительно события
называется вероятность осуществления
события при условии, что событие
уже произошло.
Слайд 46Пример. Слово “лотос” составлено из одинаковых букв- кубиков. Кубики рассыпаны. Берут
Решение: - проявиться слово «сто»
- первой извлечена “с”
- второй извлечена “т”
- третьей извлечена “о”
Слайд 50Опр. События называются
независимыми, если наступление одного
не меняет шансов появления
Если события и независимы, то
Слайд 51ЗАМЕЧАНИЯ.
Для совместных событий:
Для несовместных событий:
Для независимых событий:
Для зависимых событий:
Слайд 53
Предположим, что событие может наступить только вместе с
тогда имеет место формула
Слайд 55Эта формула решает следующую задачу: пусть произведен опыт, и в результате
Сам по себе этот факт ещё не позволяет сказать, какое из событий имело место в проделанном опыте. Можно поставить следующую задачу: найти вероятности
Слайд 58
где - столько раз проводили опыт;
- вероятность появления соб. ;
- вероятность не появления соб. ,
Слайд 77Вероятность того, что частота наступления соб. в опытах
Слайд 85
Опр. Случайной называется величина, которая в результате опыта может принять то
Слайд 86
Опр. Дискретной случайной величиной называют такую случайную величину, множество возможных
Слайд 87
Опр. Непрерывной случайной величиной называют такую случайную величину, которая может принять
Слайд 91Определение.
Суммой случайных
величин
Слайд 93
Опр. Произведением случайных величин и называется случайная величина
Слайд 95Опр. Произведением случайной величины
Слайд 97
Опр. Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь
Слайд 98
Закон распределения случайной величины можно задать, как и функцию: табличным, графическим
Слайд 99
Опр. Две случайные величины называются независимыми, если закон распределения вероятностей одной
Слайд 110
Опр. Функцией распределения вероятностей случайной величины называется функция
Слайд 122Пусть -непрерывная случайная величина.
Рассмотрим вероятность попадания значений
Слайд 124
Опр. Дифференциальной функцией распределения или плотностью распределения вероятностей наз. первая производная
Слайд 131Опр. Математическим ожиданием
дискретной случайной величины наз.
сумма произведений
значений случайной величины на
соответствующие вероятности появления
этих значений:
Слайд 132Пусть случайная величина приняла значения
Причем
появилось раз,
……………………….,
появилось раз.
где
Слайд 134Опр. Математическим ожиданием непрерывной случайной величины , возможные значения
Если возможные значения принадлежат
, то
Слайд 136 1.
2.
3.Если независимые случайные
4.Если независимые случайные величины, то
5.
Слайд 141Дисперсия
Опр. Математическое ожидание квадрата отклонения СВ от
Слайд 146Опр. Начальным моментом порядка
Опр. Центральным моментом порядка СВ называется
Слайд 159Правило «трёх сигм»: если СВ распределена по нормальному закону, то отклонение
Если СВ ~ , т.е.
СВ - стандартная, то
Слайд 166Пусть имеется СВ с математическим ожиданием
Слайд 167
Если СВ , для которой существует математическое ожидание
Слайд 170 Пусть имеется бесконечная последовательность независимых случайных величин
Тогда каково бы ни было положительное число