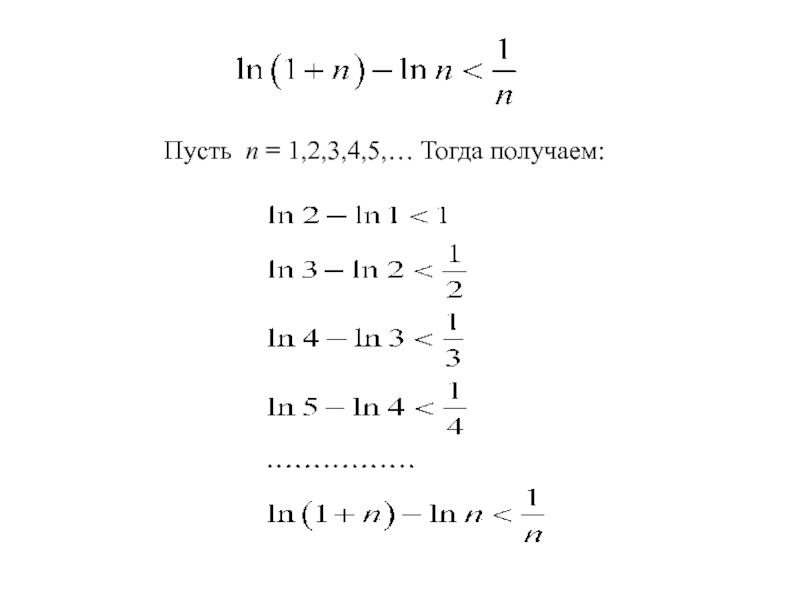- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория рядов. Числовые ряды. Признаки сходимости числовых рядов презентация
Содержание
- 1. Теория рядов. Числовые ряды. Признаки сходимости числовых рядов
- 2. Теория рядов широко используется в теоретических исследованиях
- 3. В частности, программы приближенного вычисления значений элементарных
- 4. 1. ЧИСЛОВЫЕ РЯДЫ. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ.
- 5. 1.1. Понятие о рядах Выражение вида
- 6. Сумма n первых членов ряда называется
- 7. При изменении n меняется и Sn; при
- 8. Пример 1 (бесконечно убывающая геометрическая прогрессия):
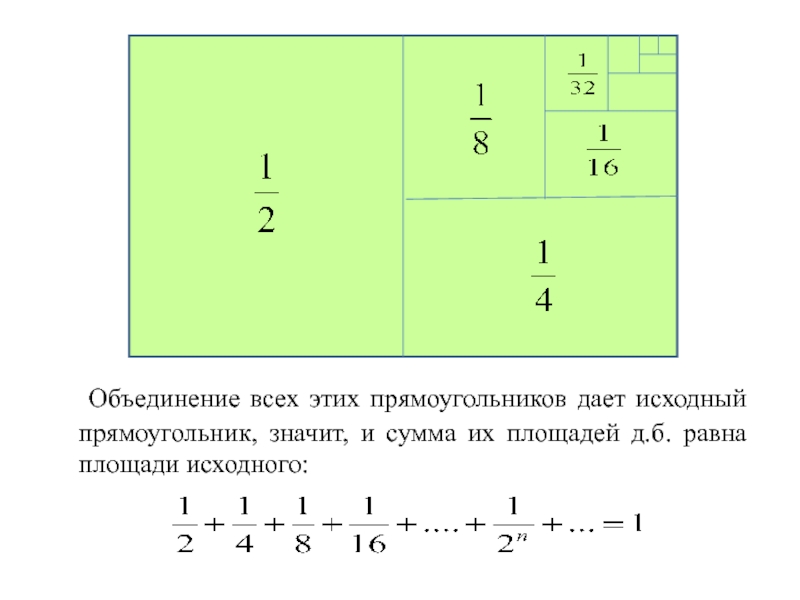
- 9. Объединение всех этих прямоугольников дает исходный
- 10. Ряд сходится, т.к. формула для геометрической прогрессии
- 11. Пример 2 (бесконечно возрастающая геометрическая прогрессия):
- 12. Ряд геометрической прогрессии
- 13. Пример 3 (гармонический ряд): Ряд расходится.
- 14. Пример 4
- 15. Пример 5 Ряд
- 16. Свойства конечных сумм , такие как ассоциативность
- 17. Свойства рядов 10. Если ряд
- 18. 10. Если ряд расходится и
- 19. Пример 7
- 20. 20. Если ряды сходятся
- 21. Пример 8
- 22. Решение Данный ряд м.б. представлен в виде или
- 23. Рассмотрим получившиеся два ряда
- 24. Следовательно, данный ряд сходится и его сумма:
- 25. 30. Если в ряде добавить
- 26. Пример 9
- 27. Сумма называется n-ым остатком ряда
- 28. Если ряд сходится, то Т.е.
- 29. Четкое определение сходимости ряда, основанное на понятии
- 30. 1.2. Необходимый признак сходимости ряда Если ряд
- 31. Пример 10
- 32. Пример 11
- 33. Пример 12
- 34. Доказательство: Прологарифмируем по основанию е:
- 36. Пусть n = 1,2,3,4,5,… Тогда получаем:
- 37. Складывая эти неравенства, получим:
- 38. Рассмотренный признак является только необходимым, но не
Слайд 2 Теория рядов широко используется в теоретических исследованиях различных вопросах естествознания и
в приближенных вычислениях. С помощью рядов вычисляются значения различных функций (логарифмических, тригонометрических, показательных и др.), вычисляются значения интегралов, решаются дифференциальные уравнения и т.п.
Слайд 3 В частности, программы приближенного вычисления значений элементарных функций и решения многих
стандартных задач, заложенные в память компьютеров и микрокалькуляторов, основаны на применении теории рядов.
Слайд 6Сумма n первых членов ряда
называется n-ой частичной суммой ряда и
обозначается
через
частичные суммы
Слайд 7 При изменении n меняется и Sn; при этом возможны два случая:
1)
величина Sn при n→∞ имеет предел S, т.е.
Тогда ряд называется сходящимся, а S- суммой ряда.
2) величина Sn при n→∞ предела не имеет или её предел равен ∞.
Тогда ряд называется расходящимся. Такой ряд суммы не имеет.
Слайд 8Пример 1
(бесконечно убывающая геометрическая прогрессия):
частичные суммы всё меньше и меньше
отличаются от 1.
Слайд 9
Объединение всех этих прямоугольников дает исходный прямоугольник, значит, и сумма их
площадей д.б. равна площади исходного:
Слайд 11Пример 2
(бесконечно возрастающая геометрическая прогрессия):
Ряд расходится, т.к
формула для геометрической прогрессии
Слайд 12Ряд геометрической прогрессии
Ряд сходится при
Ряд расходится при
( см.пример 1)
(см.
пример 2)
Слайд 15Пример 5
Ряд сходится к . Сумму
ряда нашёл Г.Лейбниц
Пример 6
Ряд сходится к . Сумму ряда нашёл Л.Эйлер
Слайд 16 Свойства конечных сумм , такие как ассоциативность (произвольная группировка членов), коммутативность
(произвольная перестановка членов), для рядов вообще говоря не имеют места.
Однако, если ряд с положительными членами сходится, то его члены м.б. сгруппированы произвольным образом- полученный ряд также сходится и имеет ту же сумму, что и данный.
Однако, если ряд с положительными членами сходится, то его члены м.б. сгруппированы произвольным образом- полученный ряд также сходится и имеет ту же сумму, что и данный.
Слайд 17Свойства рядов
10. Если ряд сходится и его сумма равна
S,
то ряд
то ряд
также сходится и его сумма равна cS.
Если все члены сходящегося ряда умножить на одно и то же число, то ряд останется сходящимся, а его сумма умножится на это число.
Слайд 19Пример 7
Известно, что ряд
сходится. Показать, что сходится
и ряд
Последний ряд получился из первого умножением на с=24
Слайд 2020. Если ряды
сходятся и их суммы равны соответственно S’
и S’’,то
и каждый из двух рядов сходится и
сумма каждого равна соответственно S’∓S’’.
и каждый из двух рядов сходится и
сумма каждого равна соответственно S’∓S’’.
Сходящиеся ряды можно почленно складывать и вычитать.
Слайд 23
Рассмотрим получившиеся два ряда
и
Т.к. они являются рядами убывающей геометрической
прогрессии, то они сходятся и их суммы равны соответственно:
Слайд 2530. Если в ряде
добавить или отбросить конечное число членов, то
полученный ряд сходится или расходится одновременно с данным.
В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов.
В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов.
Слайд 26Пример 9
Известно, что ряд
сходится. Тогда сходящимся является
и ряд:
который получается из данного отбрасыванием и добавлением конечного числа членов.
Слайд 27Сумма
называется n-ым остатком ряда
Т.к. остаток получается из
данного ряда отбрасыванием, а данный ряд из остатка- добавлением конечного числа членов, то согласно свойству 30, они одновременно сходятся или расходятся.
Слайд 28Если ряд сходится, то
Т.е. остаток стремится к нулю при неограниченном
возрастании n.
В вопросах приближенного вычисления важную роль играет оценка точности приближения.
Если значение данной величины представлено в виде ряда, то оценку приближения при помощи частичных сумм можно получить путем исследования остатка ряда.
В вопросах приближенного вычисления важную роль играет оценка точности приближения.
Если значение данной величины представлено в виде ряда, то оценку приближения при помощи частичных сумм можно получить путем исследования остатка ряда.
Слайд 29 Четкое определение сходимости ряда, основанное на понятии предела последовательности частичных сумм,
появилось лишь в начале XIX века. Тогда же началось систематическое изучение рядов.
Слайд 301.2. Необходимый признак сходимости ряда
Если ряд
сходится, то его общий член
un→0 при неограниченном возрастании n (n→∞)
Если или не существует, то ряд
расходится
Слайд 31Пример 10
Известно, что ряд
сходится. Проверим необходимое условие
Необходимое условие выполнено.
Слайд 33Пример 12
Известно, что ряд
гармонический .
Необходимое условие сходимости ряда
выполняется:
Между тем этот ряд расходится.
Слайд 37
Складывая эти неравенства, получим:
Sn- частичная сумма гармонического ряда
Поскольку
то
Ряд расходится.
Слайд 38 Рассмотренный признак является только необходимым, но не является достаточным.
Иными словами:
нарушение этого условия гарантирует расходимость ряда, но его выполнение не гарантирует сходимости!
