- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности презентация
Содержание
- 1. Теория поверхностей. Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности
- 2. Определение: проекция вектора кривизны кривой, лежащей на
- 3. Нормальная кривизна линии на поверхности. Вторая квадратичная
- 4. Нормальная кривизна линии на поверхности. Вторая квадратичная
- 5. Вычисление коэффициентов второй квадратичной формы (19)
- 6. Вычисление коэффициентов второй квадратичной формы
- 7. Вычисление коэффициентов второй квадратичной формы Пусть две
- 8. в этой точке, следовательно: Ч.т.д.
Слайд 1ТЕОРИЯ ПОВЕРХНОСТЕЙ
Нормальная кривизна линии на поверхности. Вторая квадратичная форма поверхности
Слайд 2Определение: проекция вектора кривизны кривой, лежащей на
точке кривой называется нормальной кривизной
кривой.
Пусть кривая на поверхности задана уравнением:
- вектор кривизны кривой;
– вектор нормали к поверхности,
(15) – единичный вектор нормали.
(15)
Нормальная кривизна линии на поверхности. Вторая квадратичная форма
Слайд 3Нормальная кривизна линии на поверхности. Вторая квадратичная форма
- нормальная кривизна кривой
Слайд 4Нормальная кривизна линии на поверхности. Вторая квадратичная форма
(16)
Учитывая обозначения (16) получим:
и
тогда
(17)
(18)
(18) – формула второй квадратичной формы поверхности.
Слайд 5Вычисление коэффициентов второй квадратичной формы
(19)
С другой стороны,
продифференцируем по u
(20)
Слайд 6Вычисление коэффициентов второй квадратичной формы
(21)
так как
Утверждение 2.
Нормальные кривизны двух кривых
через точку Р и имеющих в этой точке общую касательную, в
точке Р равны между собой.
Доказательство:
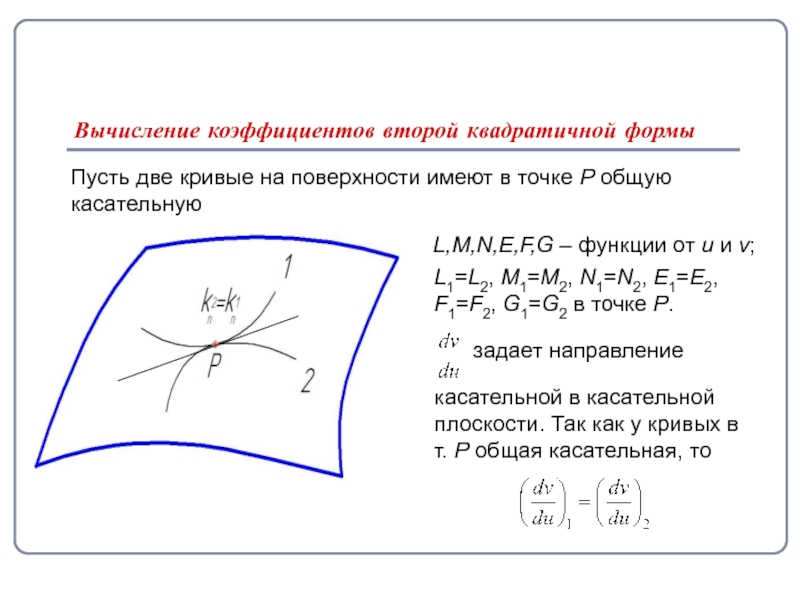
Слайд 7Вычисление коэффициентов второй квадратичной формы
Пусть две кривые на поверхности имеют в
касательную
L,M,N,E,F,G – функции от u и v;
L1=L2, M1=M2, N1=N2, E1=E2,
F1=F2, G1=G2 в точке Р.
задает направление
касательной в касательной
плоскости. Так как у кривых в
т. P общая касательная, то
Слайд 8в этой точке, следовательно:
Ч.т.д.
Определение: нормальная кривизна кривой на поверхности в
данной точке называется нормальной кривизной
поверхности в данной точке в данном
направлении касательной плоскости.
Вычисление коэффициентов второй квадратичной формы