- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория кривых. Сопровождающий трехранник презентация
Содержание
- 1. Теория кривых. Сопровождающий трехранник
- 2. Сопровождающий трехгранник кривой Определение: прямая,
- 3. Сопровождающий трехгранник Определение: касательная, главная нормаль и
- 4. Сопровождающий трехгранник Определение: плоскость, содержащая касательную и
- 5. Касательный вектор Пусть кривая задана
- 6. Касательный вектор При стремлении Δt к нулю
- 7. Уравнение касательной - радиус- -вектор точки
- 8. Уравнение касательной тогда и только тогда, когда
- 9. Длина дуги. Натуральная параметризация Рассмотрим кривую и
- 10. Длина дуги. Натуральная параметризация , в
- 11. Длина дуги. Натуральная параметризация где
- 12. Уравнение касательной в натуральной параметризации - радиус-вектор
- 13. Уравнение главной нормали в натуральной параметризации
- 14. Уравнение бинормали в натуральной параметризации направляющий
- 15. Уравнение бинормали в натуральной параметризации следовательно, в
- 16. Уравнение нормальной плоскости в натуральной параметризации
- 17. Уравнение соприкасающейся плоскости в натуральной параметризации
- 18. Уравнение соприкасающейся плоскости в натуральной параметризации 2
- 19. Уравнение спрямляющей плоскости в натуральной параметризации -
- 20. Сопровождающий трехгранник в произвольной параметризации Пусть кривая
- 21. Сопровождающий трехгранник в произвольной параметризации Вектора
- 22. Сопровождающий трехгранник в произвольной параметризации Определение: вектора
- 23. Утверждение 1: Для того чтобы необходимо и достаточно, чтобы .
- 24. Определение: нормаль кривой, параллельная
- 25. Определение: прямая, перпендикулярная
- 26. Определение: нормаль, перпендикулярная
- 27. Определение: нормальной плоскостью кривой
- 28. Определение: плоскость, содержащая
- 29. Определение: плоскость, содержащая
- 30. Определение: прямая, перпендикулярная
- 31. Определение: нормаль кривой, параллельная
- 32. Определение: прямая, перпендикулярная
- 33. Определение: нормаль кривой, параллельная
- 34. Определение: касательной к линии L в точке
- 35. Определение: касательной к линии L в точке
- 36. Определение: нормаль, перпендикулярная
- 37. Определение: прямая, перпендикулярная
- 38. Определение: нормаль кривой, параллельная
- 39. Определение: касательной к линии L в точке
Слайд 2Сопровождающий трехгранник кривой
Определение: прямая, перпендикулярная касательной к кривой и
проходящая через
В любой точке кривой имеется бесконечно много нормалей.
Определение: нормаль кривой, параллельная вектору
называется главной нормалью.
Слайд 3Сопровождающий трехгранник
Определение: касательная, главная нормаль и бинормаль
трехгранника кривой в данной точке.
Определение: нормальной плоскостью кривой в точке Р
называется плоскость, содержащая все нормали
в данной точке.
(9) – направляющий вектор бинормали.
(9)
Определение: нормаль, перпендикулярная главной нормали,
называется бинормалью.
Слайд 4Сопровождающий трехгранник
Определение: плоскость, содержащая касательную и бинормаль,
Определение: плоскость, содержащая касательную и главную
нормаль в данной точке кривой, называется
соприкасающейся плоскостью.
Определение: нормальная, соприкасающаяся и спрямляющая
плоскости являются гранями сопровождающего
трехгранника кривой в данной точке.
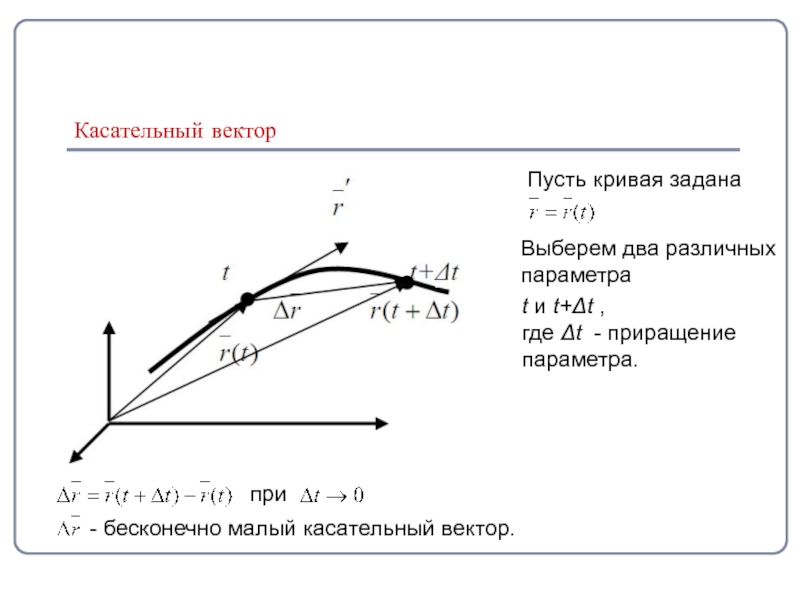
Слайд 5Касательный вектор
Пусть кривая задана
Выберем два различных
параметра
t и t+Δt ,
где Δt - приращение
параметра.
при
- бесконечно малый касательный вектор.
Слайд 6Касательный вектор
При стремлении Δt к нулю точка с параметром t+Δt устремится
точке с параметром t, и вектор
займёт своё предельное
положение и станет касательной к кривой в точке с параметром t.
Поэтому предельное значение вектора
- это касательный
вектор к кривой в точке с параметром t :
(4)
Касательный вектор
определяет направление перемещения
точки вдоль кривой для данного значения параметра t.
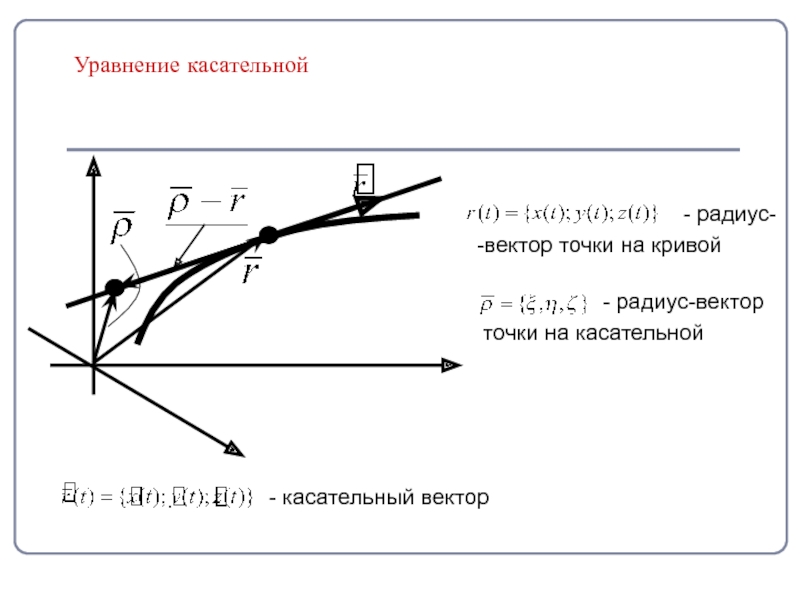
Слайд 7Уравнение касательной
- радиус-
-вектор точки на кривой
- радиус-вектор
точки на касательной
- касательный
Слайд 8Уравнение касательной
тогда и только тогда, когда пропорциональны координаты:
(5)
(5) – уравнение касательной
Слайд 9Длина дуги. Натуральная параметризация
Рассмотрим кривую и две бесконечно близкие точки.
длина пути
t до точки с параметром t+Δt.
Слайд 10Длина дуги. Натуральная параметризация
, в пределе
(6)
(7)
(7) – длина дуги кривой от
параметром t2.
Слайд 11Длина дуги. Натуральная параметризация
где
,
S – натуральный параметр на кривой.
- касательный вектор,
.
Слайд 12Уравнение касательной в натуральной параметризации
- радиус-вектор точек на касательной,
- точки
- касательный вектор;
тогда
, следовательно, можно написать в силу
пропорциональности координат:
- уравнение касательной в натуральной параметризации.
Слайд 13Уравнение главной нормали в натуральной параметризации
- направляющий вектор главной нормали,
так
,в силу утверждения 1
раздела «Векторный анализ».
- точки на кривой,
- радиус вектор точек на главной нормали,
тогда
, следовательно, в силу пропорциональности
координат можно записать:
(10)
(10) – уравнение главной нормали в натуральной параметризации.
Слайд 14Уравнение бинормали в натуральной параметризации
направляющий вектор бинормали, он должен быть
перпендикулярен
,
имеет координаты:
- радиус-вектор точек на бинормали,
- вектор бинормали,
- точки на кривой, тогда
,
Слайд 15Уравнение бинормали в натуральной параметризации
следовательно, в силу пропорциональности координат запишем:
(11)
(11) –
Слайд 16Уравнение нормальной плоскости в натуральной параметризации
- радиус вектор точек нормальной плоскости,
- направляющий вектор касательной,
- точки на кривой.
Тогда
, следовательно:
распишем это уравнение по координатам:
(12)
(12) – уравнение нормальной плоскости в натуральной
параметризации.
Слайд 17Уравнение соприкасающейся плоскости в натуральной параметризации
- вектор бинормали,
- радиус вектор
тогда
, распишем
1 способ:
, следовательно,
уравнение по координатам:
(13)
(13) – уравнение соприкасающейся плоскости в натуральной
параметризации.
Слайд 18Уравнение соприкасающейся плоскости в натуральной параметризации
2 способ:
- радиус-вектор точек соприкасающейся плоскости.
Тогда из определения соприкасающейся плоскости следует, что
вектора касательная
и главная нормаль
лежат в
соприкасающейся плоскости, тогда вектора
должны
быть компланарны, следовательно:
Распишем по координатам:
- уравнение соприкасающейся плоскости в натуральной
параметризации.
Слайд 19Уравнение спрямляющей плоскости в натуральной параметризации
- направляющий вектор главной нормали,
-
Тогда
, следовательно выполняется условие
Распишем это уравнение по координатам:
,
(14)
(14) – уравнение спрямляющей плоскости в натуральной
параметризации.
Слайд 20Сопровождающий трехгранник в произвольной параметризации
Пусть кривая задана в произвольной параметризации
.
Утверждение 1.
Вектор
лежит в соприкасающейся плоскости кривой в данной
точке.
Доказательство:
, тогда
.
Рассмотрим вектор
следовательно, вектор
,
лежит в плоскости векторов
,
т.е. в соприкасающейся плоскости.
Ч.т.д.
Слайд 21Сопровождающий трехгранник в произвольной параметризации
Вектора
лежат в соприкасающейся плоскости кривой.
(15)
перпендикулярен соприкасающейся
(15) – направляющий вектор бинормали.
- направляющий вектор касательной.
(16)
(16) – направляющий вектор главной нормали.
(17)
(17) – правая тройка векторов.
Слайд 22Сопровождающий трехгранник в произвольной параметризации
Определение: вектора
называются направляющими
векторами рёбер сопровождающего
трёхгранника.
Уравнения
произвольной параметризации выводятся аналогично, как и в
случае натуральной параметризации.
выход
Слайд 27Определение: нормальной плоскостью кривой
содержащая все нормали в данной
точке.
Слайд 28Определение: плоскость, содержащая
в данной точке кривой, называется
соприкасающейся плоскостью.
Слайд 29Определение: плоскость, содержащая
называется спрямляющей
плоскостью.
Слайд 34Определение: касательной к линии L в точке М
стремится совпасть секущая ММ’,
оставаясь на L, стремится к М –
будь то справа или слева.
Слайд 35Определение: касательной к линии L в точке М
стремится совпасть секущая ММ’,
оставаясь на L, стремится к М –
будь то справа или слева.
Слайд 39Определение: касательной к линии L в точке М
стремится совпасть секущая ММ’,
оставаясь на L, стремится к М –
будь то справа или слева.